Unit - 4
Electrical Circuits & Network Theorems
Q1) Find Current I using Superposition Theorem?
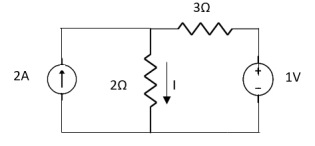
A1)
Appling Superposition theorem keeping only 1V source active
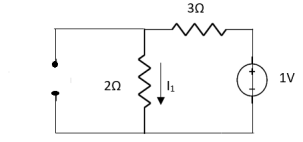

 1 =
1 = 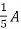
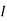 2 =
2 = 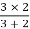
=
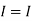 1 +
1 +  2
2
= 
Q2) Find Vth and Rth?
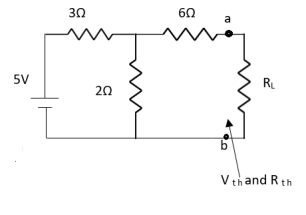
A2)

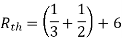
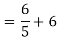
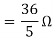


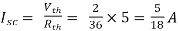
Finding Isc from circuit directly:

By KCL,
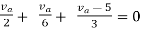
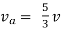
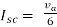

Q3) Find Rth and Vth?

A3)
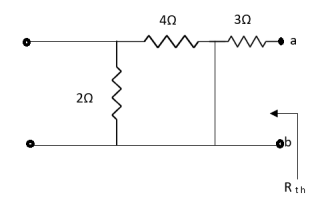

Also, clear from circuit that Vth = 1V.
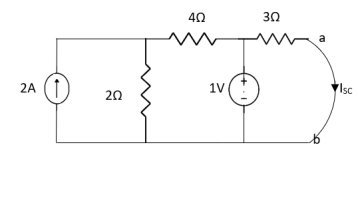
By applying KVL we get,
1-3Isc=0
Isc= A
A
Q4) Find Rth and Isc?
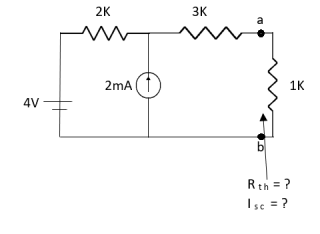
A4)
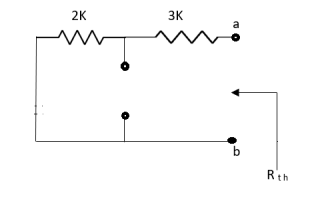
Rth=3k+2k=5k
By applying KVL we get

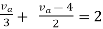
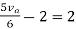


Therefore, 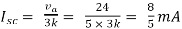
Q5) Find Vx?

A5)
For Rth
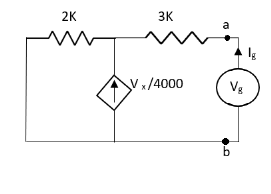
By KCL,
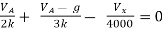


But, 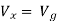
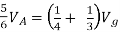

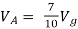
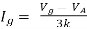
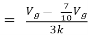
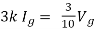

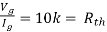
By KVL,
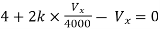
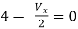


Q6) Find out the Norton’s equivalent

A6)

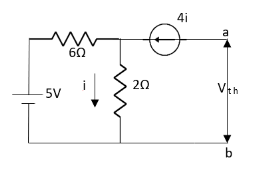
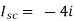
Since, there is no significance of current source
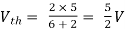
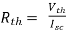
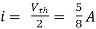

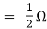
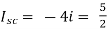 A
A
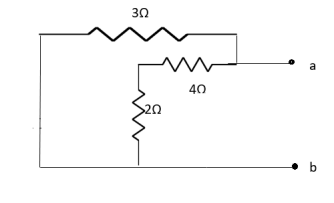
Q7) Find out the value of load resistance if power absorbed is maximum?
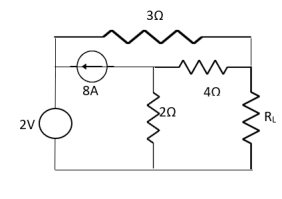
Find Thevenin’s equation
A7)
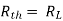


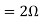

Q8) A coil takes a current of 6A when connected to 24V dc supply. To obtain the same current with 50HZ ac, the voltage required was 30V. Calculate inductance and p.f of coil?
A8)
The coil will offer only resistance to dc voltage and impedance to ac voltage
R =24/6 = 4ohm
Z= 30/6 = 5ohm
XL = 
= 3ohm
Cosφ =  = 4/5 = 0.8 lagging
= 4/5 = 0.8 lagging
Q9) The potential difference measured across a coil is 4.5V, when it carries a dc current of 8A. The same coil when carries ac current of 8A at 25Hz, the potential difference is 24V. Find current and power when supplied by 50V,50Hz supply?
A9)
R=V/I= 4.5/8 = 0.56ohm
At 25Hz, Z= V/I=24/8 =3ohms
XL = 
= 2.93ohm
XL = 2 fL = 2
fL = 2 x 25x L = 2.93
x 25x L = 2.93
L=0.0187ohm
At 50Hz
XL = 2x3 =6ohm
Z = 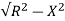 = 5.97ohm
= 5.97ohm
I= 50/5.97 = 8.37A
Power = I2R = 39.28W
Q10) A coil having inductance of 50mH an resistance 10ohmis connected in series with a 25 F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
A 10)
f0=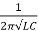 = 142.3Hz
= 142.3Hz
I0 = V/R = 200/10 = 20A
Q11) A 15mH inductor is in series with a parallel combination of 80ohm resistor and 20 F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
A11)
XL = 2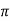 fL = 1000x15x10-3 = 15ohm
fL = 1000x15x10-3 = 15ohm
XL = 1/ C = 50ohm
C = 50ohm
Impedance of parallel combination Z = 80||-j50 = 22.5-j36
Total impedance = j15+22.5-j36 = 22.5-j21
Admittance Y= 1/Z = 0.023-j0.022 siemens
Q12) A circuit connected to a 100V, 50 Hz supply takes 0.8A at a p.f of 0.3 lagging. Calculate the resistance and inductance of the circuit when connected in series and parallel?
A12)
For series Z =100/0.8 = 125ohm
Cosφ = 
R = 0.3 x 125 = 37.5ohm
XL =  = 119.2ohm
= 119.2ohm
XL = 2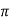 fL = 2
fL = 2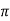 x 50x L
x 50x L
119.2 = 2 x 50x L
x 50x L
L= 0.38H
For parallel:
Active component of current = 0.8 cosφ = 0.3x0.3 = 0.24A
R = 100/0.24 =416.7ohm
Quadrature component of current = 0.8 sinφ = 0.763
XL= 100/0.763 = 131.06ohm
L= 100/0.763x2 x50 = 0.417H
x50 = 0.417H
Q13) For a series RLC circuit having R=10ohms, L= 0.15H, C=100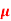 F. They are connected across 100v 50Hz supply. Calculate total impedance?
F. They are connected across 100v 50Hz supply. Calculate total impedance?
A13)
Impedance Z= 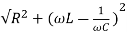
Z= 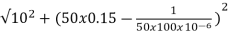 = 18.27ohm
= 18.27ohm
Q14) For a series RLC circuit having R=12ohms, L= 0.2H, C=60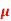 F. They are connected across 100v 50Hz supply. Calculate circuit current?
F. They are connected across 100v 50Hz supply. Calculate circuit current?
A14)
I= 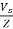
Z= 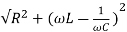
Z= 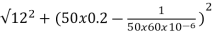 = 13.89ohm
= 13.89ohm
I = 100/13.89 =7.2A
Q15) Calculate impedance of a parallel tuned RC circuit at a frequency of 400kHz and for a BW of operation equal to 20kHz. Given R=5ohm?
A15)
BW =R/2 L
L
L= 39 H
H
f0 = 
C = 2.6x10-9F
Z= L/RC = 3kohm
Q16) Discuss AC circuits containing pure R, Pure C and L, phasor diagram and waveform?
A16)
3 Basic element of AC circuit.
1] Resistance
2] Inductance
3] Capacitance
Each element produces opposition to the flow of AC supply in forward manner.
Reactance
- Inductive Reactance (XL)
It is opposition to the flow of an AC current offered by inductor.
XL = ω L But ω = 2 ᴫ F
 XL = 2 ᴫ F L
XL = 2 ᴫ F L
It is measured in ohm
 XL∝ FInductor blocks AC supply and passes dc supply zero
XL∝ FInductor blocks AC supply and passes dc supply zero
2. Capacitive Reactance (Xc)
It is opposition to the flow of ac current offered by capacitor
Xc = 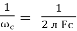
Measured in ohm
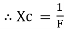 Capacitor offers infinite opposition to dc supply
Capacitor offers infinite opposition to dc supply 
Impedance (Z)
The ac circuit is to always pure R pure L and pure C it well attains the combination of these elements. “The combination of R1 XL and XC is defined and called as impedance represented as
Z = R +i X
Ø = 0
 only magnitude
only magnitude
R = Resistance, i = denoted complex variable, X =Reactance XL or Xc
Polar Form
Z =  L I
L I
Where  =
=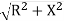
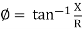 Measured in ohm
Measured in ohm
Power factor (P.F.)
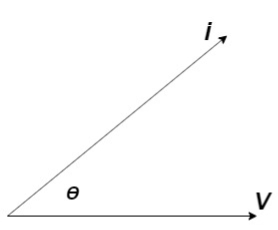
Figure: Power factor (P.F.)
It is the cosine of angle between voltage and current
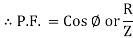
If Ɵis –ve or lagging (I lags V) then lagging P.F.
If Ɵ is +ve or leading (I leads V) then leading P.F.
If Ɵ is 0 or in phase (I and V in phase) then unity P.F.
Ac circuit containing pure resisting

Figure: Ac circuit containing pure resisting
Consider Circuit Consisting pure resistance connected across ac voltage source
V = Vm Sin ωt ①
According to ohm’s law i =  =
= 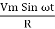
But Im = 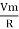
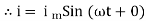 ②
②
Phases diagram
From ① and ②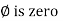 phase or represents RMD value.
phase or represents RMD value.
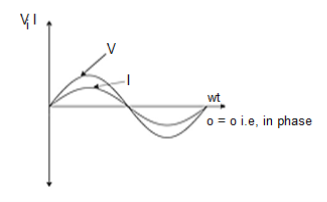
Figure: Waveform
Power P = V. i
Equation P = Vm sin ω t Im sin ω t
P = Vm Im Sin2 ω t


Average power
Pavg = 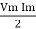
Pavg = 
Pavg = Vrms Irms
Power form [Resultant]
Figure: Power form
Ac circuit containing pure Inductors
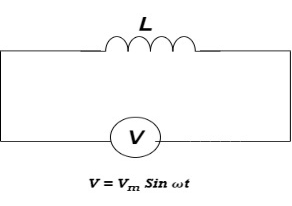
Figure: Ac circuit containing pure Inductors
Consider pure Inductor (L) is connected across alternating voltage. Source
V = Vm Sin ωt
When an alternating current flow through inductance it set ups alternating magnetic flux around the inductor.
This changing the flux links the coil and self-induced emf is produced
According to faradays Law of E M I
e = 
At all instant applied voltage V is equal and opposite to self-induced emf [ lenz’s law]
V = -e
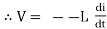 =
= 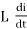
But V = Vm Sin ωt
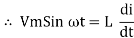
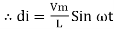 dt
dt
Taking integrating on both sides
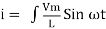 dt
dt
 dt
dt

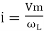 (-cos
(-cos 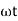 )
)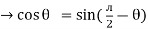

But sin (–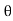 ) = sin (+
) = sin (+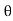 )
)
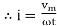 sin (
sin ( -
- 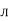 /2)
/2)
And Im= 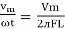
 /2)
/2)
 /2
/2
= -ve
= lagging
= I lag v by 900

Figure: Phasor
Phasor:

Figure: Phasor
Power P = Ѵ. I
= Vm sin wt Im sin (wt 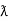 /2)
/2)
= Vm Im Sin wt Sin (wt –  /s)
/s)
 ①
①
And
Sin (wt - 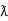 /s) = - cos wt ②
/s) = - cos wt ②
Sin (wt – 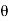 ) = - cos
) = - cos 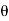
 sin 2 wt from ① and ②
sin 2 wt from ① and ②
The average value of sin curve over a complete cycle is always zero
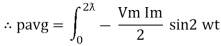
 Pavg = 0
Pavg = 0
Ac circuit containing pure capacitors:
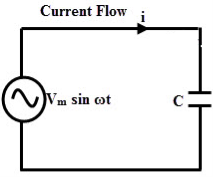
Figure: Ac circuit containing pure capacitors
Consider pure capacitor C is connected across alternating voltage source
Ѵ = Ѵm Sin wt
Current is passing through capacitor the instantaneous charge ɡ produced on the plate of capacitor
ɡ = C Ѵ
ɡ = c Vm sin wt
The current is rate of flow of charge
i=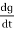 (cvm sin wt)
(cvm sin wt)
i = c Vm w cos wt
Then rearranging the above eqth.
i = 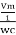 cos wt
cos wt
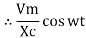
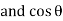 = sin (wt +
= sin (wt + 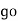 X/2)
X/2)
i = 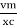 sin (wt + X/2)
sin (wt + X/2)
But 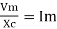
 X/2)
X/2)
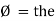
= leading
= I leads V by 900
Waveform:
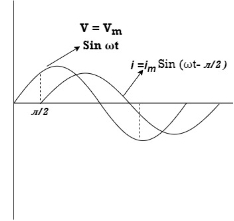
Figure: Phasor
Phase
Figure: Phasor
Power P= Ѵ. i
= [Vm sinwt] [ Im sin (wt + X/2)]
= Vm Im Sin wt Sin (wt + X/2)]
 (cos wt)
(cos wt)
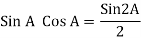
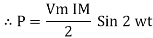
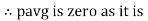 to charging power waveform [resultant].
to charging power waveform [resultant].

Figure: Charging and discharging
Study of reactance and impedance
Impedance (Z)
The ac circuit is to always pure R pure L and pure C it well attains the combination of these elements. “The combination of R1 XL and XC is defined and called as impedance represented as
Z = R +i X
Ø = 0
 only magnitude
only magnitude
R = Resistance, i = denoted complex variable, X =Reactance XL or Xc
Polar Form
Z = 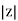 L I
L I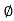
Where 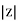 =
=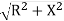
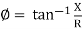 Measured in ohm
Measured in ohm
Admittance:
The reciprocal of impedance is admittance. Its unit is mho (siemens)
Y=  =
= 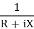
V=IZ
I=VY
Y=  =
= 
Y= G+iB
G= 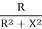
B= 
Q17) Discuss R-L-C series circuit?
A17)
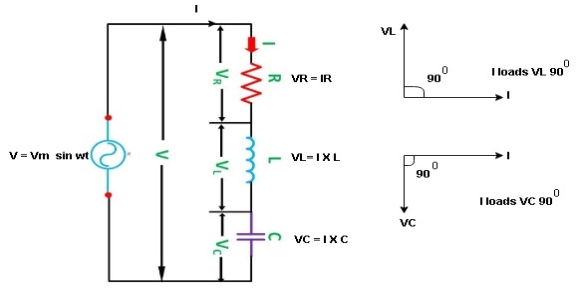
Figure: R-L-C series circuit
Consider ac voltage source V = Vm sin wt connected across combination of R L and C. When I flowing in the circuit voltage drops across each component as shown below.
VR = IR, VL = I  L, VC = I
L, VC = I  C
C
- According to the values of Inductive and Capacitive Reactance I e XL and XC decides the behaviour of R-L-C series circuit according to following conditions
① XL> XC, ② XC> XL, ③ XL = XC
① XL > XC: Since we have assumed XL> XC
 Voltage drop across XL> than XC
Voltage drop across XL> than XC
 VL> VC A
VL> VC A
- Voltage triangle considering condition A
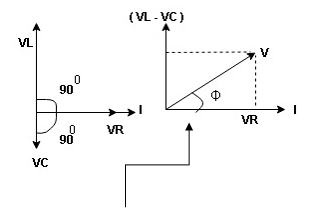
Figure: R-L-C series circuit
VL and VC are 180 0 out of phase.
Therefore cancel out each other
 Resultant voltage triangle
Resultant voltage triangle

Figure: R-L-C series circuit
Now V = VR + VL + VC c phasor sum and VL and VC are directly in phase opposition and VL
c phasor sum and VL and VC are directly in phase opposition and VL VC
VC their resultant is (VL - VC).
their resultant is (VL - VC).
From voltage triangle
V = 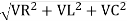
 V =
V = 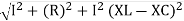
 V = I
V = I 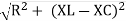

Impendence  : divide voltage
: divide voltage 
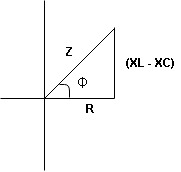
Figure: R-L-C series circuit: Impendence
Rectangular form Z = R + j (XL – XC)
Polar form Z =  l + Ø B
l + Ø B
Where  =
= 
And Ø = tan-1 
Voltage equation: V = Vm Sin wt
Current equation
i =  from B
from B
i =  L-Ø C
L-Ø C
As VL VC the circuit is mostly inductive and
VC the circuit is mostly inductive and  I lags behind V by angle Ø
I lags behind V by angle Ø
 Since i =
Since i =  L-Ø
L-Ø
 i = Im Sin (wt – Ø) from c
i = Im Sin (wt – Ø) from c

Figure: R-L-C series circuit
XC  XL: Since we have assured XC
XL: Since we have assured XC  XL
XL
 the voltage drops across XC
the voltage drops across XC  than XL
than XL
 XC
XC  XL (A)
XL (A)
 voltage triangle considering condition (A)
voltage triangle considering condition (A)
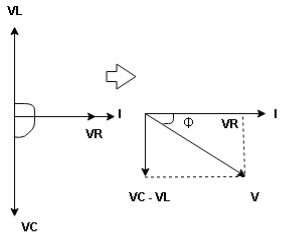
Figure: R-L-C series circuit
 Resultant Voltage
Resultant Voltage 
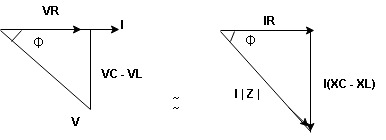
Figure: R-L-C series circuit
Now V = VR + VL + VC 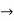 phases sum and VL and VC are directly in phase opposition and VC
phases sum and VL and VC are directly in phase opposition and VC VL
VL  their resultant is (VC – VL)
their resultant is (VC – VL)
From voltage 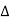
V = 
V = 
 V =
V = 
 V =
V = 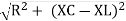
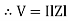
 Impedance
Impedance 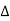 : Divide voltage
: Divide voltage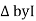
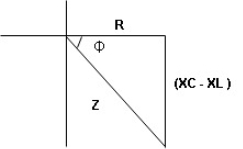
Figure: R-L-C series circuit
- Rectangular form: Z + R – j (XC – XL) – 4th quadrant
- Polar form: Z =
 L -
L -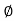
Where 
And Ø = tan-1 – 
- Voltage equation: V = Vm Sin wt
- Current equation: i =
 from B
from B - i =
 L+Ø C
L+Ø C
As VC  the circuit is mostly capacitive and
the circuit is mostly capacitive and  leads voltage by angle Ø
leads voltage by angle Ø
Since i =  L + Ø
L + Ø
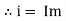 Sin (wt – Ø) from C
Sin (wt – Ø) from C
- Power
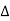 :
:
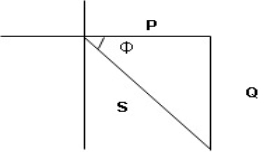
Figure: R-L-C series circuit
- XL= XC (resonance condition):
ɡȴ XL= XC then VL= VC and they are 1800 out of phase with each other  they will cancel out each other and their resultant will have zero value.
they will cancel out each other and their resultant will have zero value.
Hence resultant V = VR and it will be in phase with I as shown in below phasor diagram.
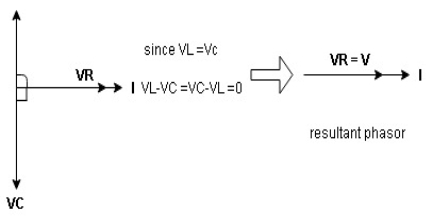
Figure: R-L-C series circuit
From above resultant phasor diagram
V =VR + IR
Or V = I  lZl
lZl
Because lZl + R
Thus Impedance Z is purely resistive for XL = XC and circuit current will be in phase with source voltage.
Since VR= V Ø is zero when XL = XC  power is unity
power is unity
Ie pang = Vrms I rms cos Ø = 1 cos o = 1
Maximum power will be transferred by condition. XL = XC
Q18) Discuss series and parallel resonance, Bandwidth and Q factor?
A18)
Series and parallel resonance
Definition: it is defined as the phenomenon which takes place in the series or parallel R-L-C circuit which leads to unity power factor
Voltage and current in R – L - C ckt. Are in phase with each other
Resonance is used in many communicate circuit such as radio receiver.
Resonance in series RLC series resonance in parallel RLC anti resonance / parallel resonance.
- Condition for resonance XL = XC
- Resonant frequency (Fr): for given values of R-L-C the inductive reactance XL become exactly aqual to the capacitive reactance Xc only at one particular frequency. This frequency is called as resonant frequency and denoted by (fr)
- Expression for resonant frequency(fr): we know thet XL = 2ƛ FL - Inductive reactance
Xc =  - capacitive reactance
- capacitive reactance
At a particular frequency ȴ = fr, the Inductive and capacitive reactance are exactly equal
 XL = XC ……at ȴ = fr
XL = XC ……at ȴ = fr
i.e  L =
L = 
 fr2 =
fr2 = 
 fr =
fr =  H2
H2
And 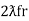 = wr =
= wr = 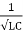 rad/sec
rad/sec
Quality factor / Q factor
The quality of resonance circuit is measured in terms of efficiency of L and C to stare energy and the efficiency of L and C to store energy as measured in terms of a factor called quality factor or Q factor it is expressed as
Q = 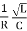 and Q =
and Q = 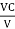
The sharpness of tuning of R-L-C series circuit or its selectivity is measured by value of Q. As the value of Q increases, sharpness of the curve also increases and the selectivity increases.
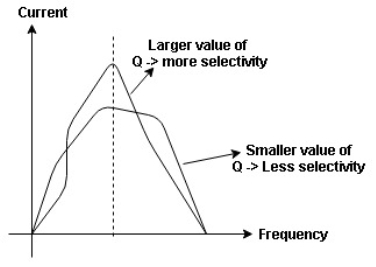
Figure: Quality factor / Q factor

Figure: Bandwidth (BW)
Bandwidth (BW) = f2 = b1
 and
and  are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance
are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance  these frequency are called as half power frequency
these frequency are called as half power frequency
Bw = fr/Q
Resonance in Parallel circuit:
When a coil is in parallel with a capacitor, as shown below. The circuit is said to be in resonance.

Figure: Resonance in Parallel circuit
The resonant frequency for above circuit is fr =  Hz
Hz
The current at resonance is I=
The value L/RC is known as dynamic impedance.
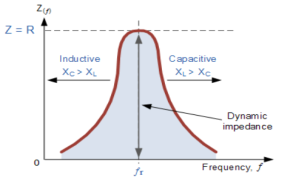
Figure: Resonance in Parallel circuit
The current at resonance is minimum. The circuits admittance must be at its minimum and one of the characteristics of a parallel resonance circuit is that admittance is very low limiting the circuits current. Unlike the series resonance circuit, the resistor in a parallel resonance circuit has a damping effect on the circuit bandwidth making the circuit less selective.
Also, since the circuit current is constant for any value of impedance, Z, the voltage across a parallel resonance circuit will have the same shape as the total impedance and for a parallel circuit the voltage waveform is generally taken from across the capacitor.
Bandwidth and selectivity:
 and
and  are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance
are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance  these frequency are called as half power frequency
these frequency are called as half power frequency
Bw = fr/Q
Q = 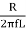 =
=  fCR = R
fCR = R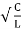
Resonant Frequency:
The resonant frequency for parallel resonant circuit is given as
fR= 
Where L= inductance of the coil
C = is the capacitance
Rs = Resistive value of coil.
Q19) Discuss ideal constant-voltage and constant-current sources?
A19)
Ideal and practical Voltage and Current source:
A voltage source is a device which provides a constant voltage to load at any instance of time and is independent of the current drawn from it. This type of source is known as an ideal voltage source. Practically, the ideal voltage source cannot be made. It has zero internal resistance. It is denoted by this symbol.

Figure: Voltage source symbol
Ideal Voltage Source

Figure: Ideal Voltage Source
The graph represents the change in voltage of the voltage source with respect to time. It is constant at any instance of time.
Voltage sources that have some amount of internal resistance are known as a practical voltage source. Due to this internal resistance, voltage drop takes place. If the internal resistance is high, less voltage will be provided to load and if the internal resistance is less, the voltage source will be closer to an ideal voltage source. A practical voltage source is thus denoted by a resistance in series which represents the internal resistance of source.
Practical Voltage source
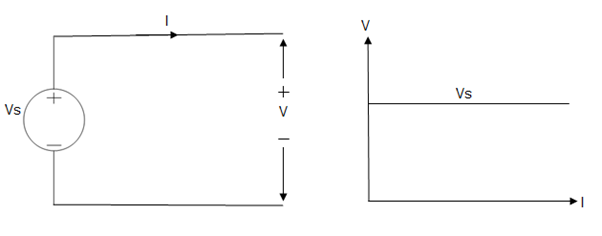
Figure: Practical Voltage source
The graph represents the voltage of the voltage source with respect to time. It is not constant but it keeps on decreasing as the time passes.
Current source
A current source is a device which provides the constant current to load at any time and is independent of the voltage supplied to the circuit. This type of current is known as an ideal current source; practically ideal current source is also not available. It has infinite resistance. It is denoted by this symbol.
Ideal Current source

Figure: Ideal Current source
The graph represents the change in current of the current source with respect to time. It is constant at any instance of time.
Why ideal Current source has infinite resistance?
A current source is used to power a load, so that load will turn on. We try to supply 100% of the power to load. For that, we connect some resistance to transfer 100% of power to load because the current always takes the path of least resistance. So, in order for current to go to the path of least resistance, we must connect resistance higher than load. This is why we have the ideal current source to have infinite internal resistance. This infinite resistance will not affect voltage sources in the circuit.
Practical Current source
Practically current sources do not have infinite resistance across there but they have a finite internal resistance. So the current delivered by the practical current source is not constant and it is also dependent somewhat on the voltage across it.
A practical current source is represented as an ideal current source connected with resistance in parallel.
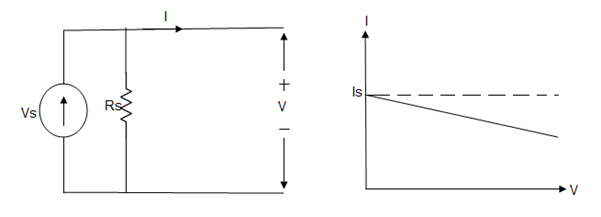
Figure: Practical Current source
The graph represents the current of the current source with respect to time. It is not constant but it also keeps on decreasing as the time passes.
Examples of current and voltage sources
The examples of current source are solar cells, transistors and examples of some voltage sources are batteries and alternators.
This was all about ideal and practical sources of power. The ideal sources are very useful for calculations in theory but as ideal sources are not practically possible, only practical sources are used in practical circuits. The batteries we use are a practical source of power and the voltage and current decreases as we use it. Thus both are useful to us in their own ways.

Figure: Examples of current and voltage sources
Q20) Discuss Reciprocity Theorem?
A20)
Reciprocity Theorem states that, the value of current due to a single source in any particular branch of circuit is equal to the value of current in the original branch where the source was placed when the source is shifted to that particular branch of circuit. This theorem is only applicable for a reciprocal network i.e. linear and bilateral circuit having only one independent source. This theorem can, however, be used for both AC and DC circuit.
In simple words, we can state the reciprocity theorem as when the places of voltage and current source in any network are interchanged the amount or magnitude of current and voltage flowing in the circuit remains the same.
The location of the voltage source and the current source may be interchanged without a change in current. However, the polarity of the voltage source should be identical with the direction of the branch current in each position.
The Reciprocity Theorem is explained with the help of the circuit diagram shown below
Figure: Circuit diagram
The various resistances R1, R2, R3 is connected in the circuit diagram above with a voltage source (V) and a current source (I). It is clear from the figure above that the voltage source and current sources are interchanged for solving the network with the help of Reciprocity Theorem.
The limitation of this theorem is that it is applicable only to single-source networks and not in the multi-source network. The network where reciprocity theorem is applied should be linear and consist of resistors, inductors, capacitors and coupled circuits. The circuit should not have any time-varying elements.
Steps for Solving a Network Utilizing Reciprocity Theorem
- Firstly, select the branches between which reciprocity has to be established.
- The current in the branch is obtained using any conventional network analysis method.
- The voltage source is interchanged between the branch which is selected.
- The current in the branch where the voltage source was existing earlier is calculated.
- Now, it is seen that the current obtained in the previous connection, i.e., in step 2 and the current which is calculated when the source is interchanged, i.e., in step 4 are identical to each other.
Q21) Discuss Maximum power transfer theorem?
A 21)
Maximum power transfer theorem states that AC voltage source will deliver maximum power to the variable complex load only when the load impedance is equal to the complex conjugate of source impedance.
Proof:
Replace any two terminal linear network or circuit to the left side of variable load resistor having resistance of RL ohms with a Thevenin’s equivalent circuit. We know that Thevenin’s equivalent circuit resembles a practical voltage source.
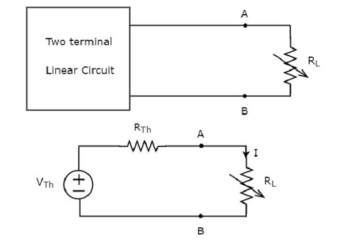
Figure: Maximum power transfer theorem
The amount of power dissipated across the load resistor is
PL = I 2 R L ----------------------(1)
Substitute I = Vth / Rth + RL
PL = Vth / (Rth + RL ) 2 RL
PL = Vth 2 { RL / (RTH + RL) 2 ------------------------------(2)
Condition for Maximum Power Transfer
For maximum or minimum, first derivative will be zero. So, differentiate Equation 1 with respect to RL and make it equal to zero.
DPL / d RL = V Th 2 { (Rth + RL) 2 x 1 -RL x 2(Rth + RL) / (Rth + RL) 4 } =0
(Rth + RL) 2 – 2RL (Rth + RL) = 0
(Rth + RL) (Rth + RL – 2 RL) = 0
Rth - RL = 0
Rth = RL or RL = Rth
Therefore, the condition for maximum power dissipation across the load is RL=RTh. That means, if the value of load resistance is equal to the value of source resistance that is Thevenin’s resistance, then the power dissipated across the load will be of maximum value.
Substitute RL = Rth and PL = PL,max
PL,max = V th 2 { Rth / (Rth + Rth ) 2 }
= V th 2 ( Rth / 4 Rth 2 )
= V th 2 / 4 Rth
PL,max = V th 2 / 4 RL [RL = Rth]
Efficiency of Maximum power transfer
= PL,max/ Ps
PL,max = maximum amount of power transferred to the load
Ps = amount of power generated by the source.
The amount of power generated by the source is
Ps = I2 Rth + I2 RL
Ps = 2 I2 Rth ; since RL = Rth
Substitute I = Vth / 2 Rth
Ps = 2(Vth / 2Rth) 2 Rth
Ps = 2(Vth / 4Rth) 2 Rth
Ps = Vth 2 / 2 Rth
Substituting with PL max and Ps
= (Vth 2 / 4 Rth) / (Vth 2 / 2 Rth)
max = ½
Q22) Discuss Applications to DC and AC circuits?
A22)
Applications to DC circuits
All electronics projects and parts for sale on Spark Fun run on DC. Everything that runs off of a battery, plugs into the wall with an AC adapter, or uses a USB cable for power relies on DC.
- Batteries: Batteries, both non-rechargeable and re-chargeable can only supply direct current. The rechargeable batteries also need recharging using direct current.
- Electronic equipment: All equipment like computers, radios, mobile phones, and in fact all electronic equipment uses direct current to power the electronic circuits. Bipolar transistors, FETs and the integrated circuits that use these components all need direct current to power them and will damaged if a reverse polarity is supplied. Although many of these items are powered by AC mains, there is a unit called a power supply within the unit that converts the incoming AC to direct current with the right voltage(s) within the electronic item.
- Some electrical equipment: Although a lot of electrical equipment uses AC, some uses direct current.
- Solar panels: Solar panels used for generating electricity produce direct current directly from the solar panels themselves. When used with AC mains to feed into the mains or supply local AC power for AC supplies, a unit known as an inverter is required to enable the direct current, DC from the solar panels to be converted to AC.
Applications to AC circuits
Home and office outlets are almost always used in AC. This is because generating and transporting AC across long distances and relatively easy. At high voltages like as over 110kV, less energy is lost in electrical power transmission. Higher voltages mean lower currents, and lower currents mean less heat generated in the power line due to resistance. AC can be converted from high voltages easily using transformers.
AC is also capable of powering electric motors. Motors and generators are the exact same device, but motors convert electrical energy into mechanical energy. This is useful for many large appliances like refrigerators, dishwashers, and so on, which run on AC.
Alternating current tends to be used for power distribution. It has the advantage that it can easily be converted to other voltages using a simple transformer - transformers do not work with direct current.
In view of the fact that alternating current is used for the supply system, it is also used in motors, for heating and for many other items without the need for it to be converted to direct current
Q23) Discuss transient currents growth and decay of current in RL?
A23)
Transient phenomena are phenomena that exist only for short a while and are not simple periodic functions of time.
Transient currents and voltages: Production of currents and voltages in a circuit in a very short interval of time is called transient currents and voltages. During the transient process, the currents and voltages in the circuit are functions of time.
Growth and decay of current in L-R circuit
(i) Growth of current in L-R circuit.
Consider a circuit consisting of a battery of a steady emf E, an inductance L and a resistance R as shown in Figure.

Figure: Growth of current in L-R circuit
When the key is suddenly pressed, there is growth of current in the circuit and a back emf is induced. Let I be the current at any instant of time t then
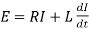 ……….. (1)
……….. (1)
When the current reaches maximum value I0, the back emf
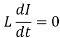
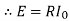 ……….. (2)
……….. (2)
From eqns (1) and (2), we have
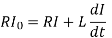
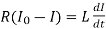 ……….. (3)
……….. (3)
Taking (I0 – I) = x
Differentiating with respect to time, we get
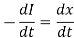
Substituting this in eq. (3), we get
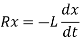

Integrating
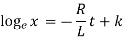
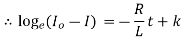
Where K is constant.
When t = 0, I = 0,
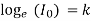
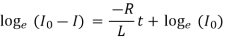
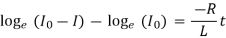


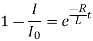
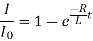

The quantity L/R is called the time constant of the circuit.
Time constant
The quantity R
L has the dimension of time and is called the time constant () of the
L-R circuit.
If L/R = t, then
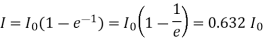
The time constant L/R of a L-R circuit is the time taken by the current to grow from zero to 0.632 times the maximum value of current - I0 in the circuit. The graph between current and time at the time of the growth of current is shown in figure

Figure: Growth of current in L-R circuit
Decay of current in a circuit containing L and R
When the circuit is broken, an induced emf, equal to -L (dI/dt)is again produced in the inductance L and it slows down and decay to zero. The current in the circuit decays from maximum value I0 to zero.
During the decay, let I be the current at time t. In this case E=0. The emf equation for the decay of current is
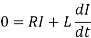
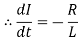
Integrating

Where k is constant
When t=0, I=I0

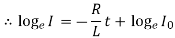



Equation represents the current at any instant t during decay. A graph between current and time during decay is shown in Figure.
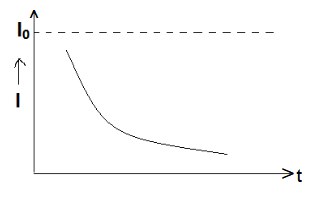
Figure: Decay of current in a circuit containing L and R
Time constant
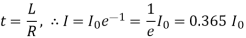
The time constant L/R of a L-R circuit may also be defined as the time in which the current in the circuit falls to 1/e of its maximum value when emf is removed. Figure shows that the growth and decay curves are complementary with each other.

Figure: Time constant
Q24) Discuss transient currents growth and decay of current in RC?
A24)
Transient phenomena are phenomena that exist only for short a while and are not simple periodic functions of time.
Transient currents and voltages: Production of currents and voltages in a circuit in a very short interval of time is called transient currents and voltages. During the transient process, the currents and voltages in the circuit are functions of time.
CHARGE AND DISCHARGE OF A CAPACITOR THROUGH A RESISTOR
(i) Growth of charge
Consider a circuit consisting of a cell of emf E, a key K, a capacitor C and a resistance R as shown in Figure.
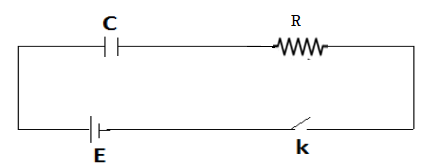
Figure: CR Circuit
When the current is started, let q be the instantaneous charge on the condenser and I be the instantaneous current. The emf equation for the CR circuit is

But 
Hence, 




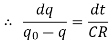
Integrating,

Where K is a constant
Applying the initial condition, When t=0, q=0, -logeq0=K
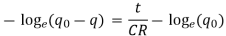
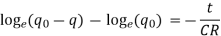
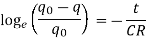
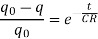

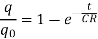
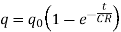
This is called instantaneous value of the charge at time t. The term CR is called time constant of the circuit.
Time constant
At the end of time t = CR,
The Eq. Becomes
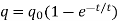
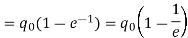
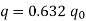
Thus, the time constant may be defined as the time taken by the capacitor to get charged to 0.632 times its maximum value. The growth of charge is shown in Figure.

Figure: Growth of charge
Decay of charge (Discharging of a capacitor though Resistance)
Let the capacitor having charge q0 be now discharged by opened the key K. The charge flows out of the capacitor. In this case E = 0. The emf equation is
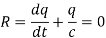

Integrating,

Where K is a constant
Initial condition, when t = 0, q = q0

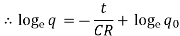


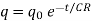
This is called the instantaneous value of the charge during the discharge. The graph for decay of charge is shown in Figure.
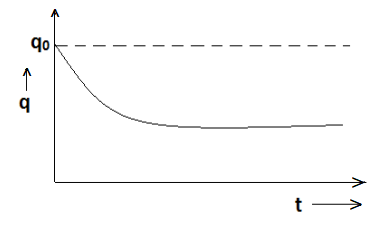
Figure: Decay of charge
Time constant: If we put t = CR in Equation, we get q = q0e-1
Ieq = q0 x 1/e, q = 0.368 q0
Hence time constant may also be defined as the time taken by the capacitor to discharge the charge from 0.368 of its maximum value.