Unit - 1
Atomic Spectra and Models
Q1) Explain Inadequacy of classical physics.
A1)
The explanation of classical physics: When an electric charge vibrates, it produces light, which is an electromagnetic wave. (The term "vibrates" refers to any change in the charge's motion, such as speeding up, slowing down, or changing direction.) Remember that heat is nothing more than the kinetic energy of random motion. Electrons vibrate in random directions in a heated object, producing light as a result. A hotter object produces more energetic vibrations, which results in more light being emitted —- it lights brighter. So far, everything has gone well. Classical physics, on the other hand, was unable to explain the form of the blackbody spectrum.
A heated object's electrons can vibrate at a variety of frequencies, from a few vibrations per second to thousands of vibrations per second. In reality, there is no limit to the frequency that can be used. According to classical physics, each vibration frequency should have the same energy. Because the frequency has no upper limit, the energy of the vibrating electrons at high frequencies has no upper limit. This indicates that, according to classical physics, the energy of light produced by electrons vibrating at high frequencies has no limit. The blackbody spectrum always becomes smaller on the left-hand side in experiments (short wavelength, high frequency).
Max Planck came up with the solution in 1900. He claimed that the traditional concept that each vibration frequency should have the same energy was incorrect. Instead, he claimed that electrons vibrating at various frequencies do not share energy evenly. Energy, according to Planck, arrives in clumps. A clump of energy was dubbed a quantum by him. The size of a clump of energy —- a quantum —- is determined by the vibration frequency. Planck's rule for a quantum of energy for a vibrating electron is as follows:
Quantum energy = (a calibration constant) x (frequency of vibration)
Or
Hf = E
The calibration constant, h, is now known as Planck's constant. It’s worth is approximately 6 x 10-34, which is quite small!
So, how does this explain the blackbody radiation spectrum? According to Planck, an electron vibrating at frequency f could only have an energy of 1 hf, 2 hf, 3 hf, 4 hf, and so on; that is, an electron vibrating at frequency f could only have an energy of 1 hf, 2 hf, 3 hf, 4 hf, and so on.
(Any integer) x hf = energy of a vibrating electron
If the electron is to vibrate, it must have at least one quantum of energy. If it doesn't have at least 1hf of energy, it won't vibrate and won't be able to create any light. Exclaimed Planck, "the amount of energy in a quantum, hf, is so great at high frequencies that the high-frequency vibrations can never get underway!" This is why the left-hand (high frequency) side of the blackbody spectrum is always narrow.
Q2) How is Radiation Absorbed?
A2)
What exactly does "black body" radiation imply? The argument is that the radiation emitted by a heated body is influenced by the body being heated to some amount. Let's take a step back for a moment and analyse how different materials absorb radiation. Some, such as glass, appear to absorb very little light and let it pass right through. A gleaming metallic surface does not absorb light; instead, it reflects it. Light and heat are almost fully absorbed by a black material like soot, and the material becomes warm. How can we explain these diverse behaviours in terms of light interacting with charges in the material, causing these charges to oscillate and absorb energy from the radiation? In the case of glass, this clearly does not occur, at least not frequently. What's to stop you? Quantum mechanics is required to fully comprehend why, but the fundamental notion is that there are charges—electrons—in glass that can oscillate in response to an applied external oscillating electric field, but these charges are strongly linked to atoms and can only oscillate at particular frequencies. (These charge oscillations occur as an electron jumps from one orbit to another, according to quantum experts.) Of course, in the 1890s, when the first precision work on black body radiation was being done, this was not understood.) Because none of these frequencies correlate to visible light in regular glass, there is no resonance with a light wave, and thus minimal energy is absorbed. As a result, glass is ideal for windows! That's a given. Glass, on the other hand, is opaque at frequencies outside the visual range (in general, both in the infrared and the ultraviolet). These are the natural oscillation frequencies of the electrical charge distributions in atoms or bonds.
How can we comprehend how a metal surface reflects light? Electrons in a piece of metal are free to move across the entire solid. This is what distinguishes a metal from other materials: it easily transmits both electricity and heat, which are conveyed by currents of freely moving electrons. (Well, vibrations do carry a small amount of heat.) Metals, on the other hand, are easily identifiable due to their lustrous appearance—why is that? Again, it's those free electrons: the electrical field of the incoming light wave drives them into enormous (compared to the atoms) oscillations, and this generated oscillating current radiates electromagnetically, exactly like a current in a transmitting antenna. The reflected light is the source of this radiation. Little of the incoming radiant energy is absorbed as heat by a polished metal surface; instead, it is reradiated, or reflected.
Consider a substance that absorbs light and does not transmit or reflect it. With soot, we're quite near to perfect absorption. It will conduct an electric current like a metal, but not nearly as effectively. Unattached electrons can flow across the entire solid, but they constantly collide with objects because they have a short mean free path. They create vibration when they bump, similar to balls hitting bumpers in a pinball machine, and hence release kinetic energy as heat. Although the electrons in soot have a shorter mean free path than those in a good metal, they travel far more freely than electrons attached to atoms (as in glass), allowing them to accelerate and absorb energy from the light wave's electric field. As a result, they are extremely efficient at converting energy from light waves to heat.
Q3) What about Equipartition of Energy?
A3)
The energy equipartition is a key conclusion of classical statistical mechanics: for a system in thermal equilibrium, each degree of freedom has an average energy of 12kBT. (Boltzmann's constant is kB.) Thus molecules in a gas have average kinetic energy 32kBT, 12kBT for each direction, and a simple one-dimensional harmonic oscillator has total energy kBT: 12kBT kinetic energy and 12kBT potential energy.
Comparing now the formula for the number of modes N(f)Δf in a small interval Δf
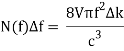
With Planck’s formula for radiation energy intensity in the same interval:
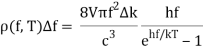
For the low frequency modes hf≪kBT we can make the approximation
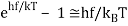
And it follows immediately that each mode has energy kBT, in line with classical predictions.
However, things go horribly wrong on a regular basis! The number of modes grows indefinitely, but the energy in these high-frequency modes decreases exponentially as the frequency rises. This was eventually termed the UV catastrophe by Ehrenfest. Rayleigh's sound strategy didn't appear to be that sound after all—something vital was lacking.
Planck never discussed equipartition, which is maybe unexpected. Of fact, as Rayleigh pointed out, equipartition was recognised to have issues, such as in the case of gas specific heat. In truth, Planck was unsure about the existence of atoms, writing subsequently that “I had been inclined to oppose atomism” in the 1890s (see notes). Even Boltzmann was unclear how successfully oscillators achieved thermal equilibrium with electromagnetic radiation—after all, it was well known that diatomic molecules oscillated with kinetic energy but did not achieve classical thermal equilibrium. (Maxwell observed that hot gases generate light at specific frequencies as early as 1877.) The oscillations must be simple harmonic because the frequencies do not change with temperature—but such an oscillator would surely be activated by collisions at low temperatures, so why wasn't energy delivered into this mode?)
Q4) Short Note on Wien’s Displacement Law.
A4)
Wien's Displacement Law is easily deduced from Planck's formula: the highest radiation per unit frequency range occurs at the frequency f for which the function f3/(ehf/kBT1) is at its maximum. Numerically, hfmax=2.82kBT is obtained.
The equation linking the frequency of maximum energy intensity in units of Joules/m3/Hz may be established theoretically (and is proven experimentally) as fmax=5.881010 T Hz/K.
The law is frequently expressed in terms of the wavelength at which the intensity, now measured in Joules/m3/m, or per unit interval of wavelength, and
2.910-3 TmK is the maximum value.
The crucial thing to remember here is that these calculations do not produce the same result, as can be easily confirmed, because fmaxmax1.7108m/sec is not the same as the speed of light! Because the two measurements, per unit interval of frequency and per unit interval of wavelength, are distinct, a claim that, for example, sunlight is most intense in the yellow must explain which one is being utilised (actually it would be wavelength, frequency would give the near infrared).
An Excel spreadsheet was used to create the graphs of black body radiation as a function of temperature. You are invited to download and experiment with this spreadsheet to see how radiation varies with temperature. It's simple to use—all you have to do is enter the temperature and see the graph change.
Q5) Explain the Applications of Photoelectric effect.
A5)
Photoelectric devices have a number of advantages, including creating a current that is precisely proportional to light intensity and having a very fast response time. The photoelectric cell, often known as a photodiode, is a simple device. This was originally a phototube, a vacuum tube with a metal cathode with a tiny work function that allowed electrons to be easily emitted. An anode held at a large positive voltage compared to the cathode would collect the current produced by the plate. Phototubes have been phased out in favour of semiconductor-based photodiodes, which can detect light, quantify its intensity, operate other devices in response to illumination, and convert light to electrical energy. These devices operate at low voltages, similar to their bandgaps, and are utilised in a variety of applications including industrial process control, pollution monitoring, light detection in fibre optic telecommunications networks, solar cells, imaging, and many more.
Semiconductors with bandgaps that correspond to the photon energy to be sensed make up photoconductive cells. Photographic exposure metres and automatic street lighting switches, for example, function in the visible spectrum and are often constructed of cadmium sulphide. Lead sulphide or mercury cadmium telluride can be used to make infrared detectors, such as night-vision sensors.
A semiconductor p-n junction is commonly used in photovoltaic devices. Solar cells are typically built of crystalline silicon and convert approximately 15% of incident light energy into electricity. Solar cells are frequently utilised in specialised contexts such as space satellites and remote telephone sites to produce very tiny amounts of power. Solar power may become economically viable for large-scale applications when cheaper materials and higher efficiency become available.
The photomultiplier tube is a very sensitive extension of the phototube, which contains a sequence of metal plates called dynodes and was first created in the 1930s. When light strikes the cathode, electrons are released. These are drawn to the first dynode, where they release more electrons, which then strike the second, and so on. The photocurrent is boosted so much after up to ten dynode stages that some photomultipliers can almost detect a single photon. In spectroscopic research, where it is frequently necessary to monitor extremely faint light sources, these devices, or solid-state counterparts of comparable sensitivity, are important. They're also employed in scintillation counters, which have a substance that creates light flashes when X-rays or gamma rays strike it, as well as a photomultiplier that counts and measures the strength of the flashes. These counters are employed for things like recognising certain isotopes for nuclear tracer analysis and detecting X-rays in computerised axial tomography (CAT) scans, which show a cross section of the body.
Q6) What is Compton Effect? Explain its Derivation.
A6)
The Compton effect is the phenomenon that occurs when x-rays or gamma rays are scattered on a substance with increasing wavelength. In the year 1922, Arthur Compton investigated this phenomenon. Compton discovered that wavelength is unaffected by incident radiation intensity during his research. It is determined by the scattering angle as well as the wavelength of the incident beam. It is expressed mathematically as follows:
What is the location?
The angle at which light is scattered
m0: an electron's rest mass
h/m0c : The electron's Compton wavelength
The peaks of the radiation spectrum are denoted by the letters s and 0.
Derivation of Compton effect equation
Considering the elastic collide between a photon and an electron, following is the derivation:
hν0 : energy of photon
Pi=hν0/c :momentum of the photon
Pi=pfcosΘ+pecosϕ(1) (conservation of momentum in x direction)
0=−pfsinΘ+pesinϕ(2) (conservation of momentum in y direction)
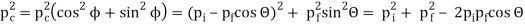
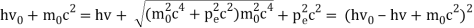

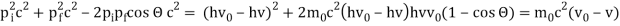
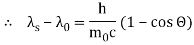
Therefore, above is the Compton effect equation andhm0c≡λc is Compton wavelength of an electron.
Q7) Difference Between Compton Effect and Photoelectric Effect.
A7)
Compton effect | Photoelectric effect |
This is the result of high-energy photons being bound to free electrons dispersing inelastically. | When electromagnetic radiation interacts with electrons, weakly bound electrons are expelled from the surface of the material, causing this effect. |
The effect was explained by Arthur Compton. | The effect was explained by Albert Einstein. |
The free electrons have a mid-energy level of energy. | The electrons have a low-energy associated with them. |
The dispersed photon has a longer wavelength than the incident photon. | The photon vanishes after interacting with the electrons, therefore the wavelength isn't visible. |
Q8) What is Wave-Particle Duality: Light?
A8)
Does light consist of particles or waves? When one focuses upon the different types of phenomena observed with light, a strong case can be built for a wave picture:


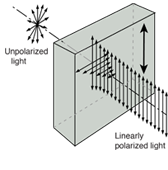
Fig. Interference Diffraction Polarization
Phenomenon | Can be explained in | Can be explained in |
Reflection |  |  |
Refraction |  |  |
Interference |  |  |
Diffraction |  |  |
Polarization |  |  |
Photoelectric effect |  |  |
Waves can explain the majority of regularly observed light phenomena. However, the photoelectric effect suggested that light has a particle nature. Then electrons were discovered to have multiple natures as well.
There is a lot of debate in the literature concerning whether light reflection and refraction can be represented in particle terms at an interface when the medium changes. Treating light as a wave phenomenon is sufficient for practical geometrical optics applications.
Q9) Define Atomic spectra and Explain Spectral Series of Hydrogen Atom.
A9)
An electron's spectrum of electromagnetic radiation released or absorbed as it moves between different energy levels within an atom.
When an electron moves from one energy level to the next, it emits or absorbs light of a given wavelength. The atomic spectra of atoms is the collection of all these unique wavelengths of the atom in a certain set of variables such as pressure, temperature, and so on. Emission spectra, absorption spectra, and continuous spectra are the three forms of atomic spectra.
Spectral Series of Hydrogen Atom
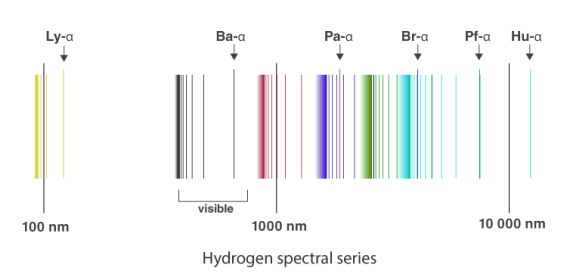
The atomic hydrogen emission spectrum is divided into a number of spectral lines with wavelengths determined by the Rydberg formula, as seen in the image above. The atomic transitions between different energy levels cause the observed spectral lines in the hydrogen emission spectrum. In astronomical spectroscopy, spectral series are crucial.
Q10) What is Hydrogen spectrum?
A10)
The hydrogen spectrum is a crucial piece of evidence for demonstrating an atom's quantized electronic structure. When an electric discharge is conducted across a gaseous hydrogen molecule, the hydrogen atoms in the molecule dissociate. The energetically excited hydrogen atoms emit electromagnetic radiation as a result of this process. The hydrogen emission spectrum is made up of discrete frequency radiation. These radiation series bear the names of the scientists who discovered them.
The spectral lines of the hydrogen atomic emission spectrum are explained by Bohr's hypothesis. The energy of an atom's electron remains unaltered while it is in the ground state. The electron jumps from the ground state orbit to a more distant excited state orbit when the atom absorbs one or more quanta of energy. The variable n is used to identify energy levels. n = 1 is the ground state, n = 2 is the first excited state, and so on. The difference in energy between the two energy levels is equal to the energy obtained by the atom. When the atom relaxes back to a lower energy state, energy equal to the difference in energy between the two orbits is released (see Figure 1).
According to the equation E = hv, the change in energy, E, causes light of a specific frequency to be emitted. Remember that the atomic emission spectrum of hydrogen has four different frequency spectral lines? The finding that electron orbits are not evenly spaced is explained in the Bohr model. The spacing between the levels gets narrower and smaller as the energy travels further away from the nucleus.
Bohr was able to calculate the energies that the hydrogen electron would have in each of its permissible energy levels using the wavelengths of the spectral lines. The energy level transitions that corresponded to the spectral lines in the atomic emission spectrum were then mathematically demonstrated ( Figure 2).
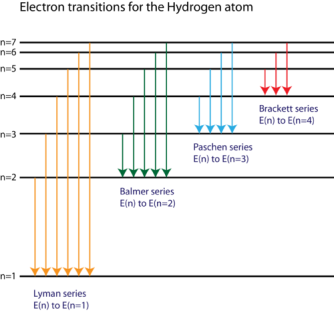
Figure. The electron energy level diagram for the hydrogen atom.
Q11) Give Explanation of the Emission Spectrum.
A11)
A theoretical explanation of the spectrum of radiation released by a glowing object was offered by Max Planck. He proposed that the walls of a glowing solid may be visualised as a set of resonators oscillating at various frequencies. These resonators absorb energy from the object's walls in the form of heat and release it in the form of electromagnetic radiation. At any given time, the energy of these resonators is proportional to the frequency with which they vibrate.
Planck had to postulate that the energy of these oscillators could only take on a restricted number of values in order to suit the observed spectrum. To put it another way, the energy spectrum for these oscillators was no longer continuous. These oscillators are theoretically "countable" since the number of possible energy levels is restricted. As a result, the energy of the oscillators in this system is quantized. To explain how light was emitted, Planck created the concept of quantization.
Planck's work was extended by Albert Einstein to include the light that had been emitted. Einstein proposed that light acted like a stream of little bundles, or packets, of energy, at a time when everyone accepted that light was a wave (and thus continuous). To put it another way, light was quantized as well. Einstein's model was predicated on two premises. To begin, he assumed that light was made up of photons, which are small, distinct energy bundles. He also assumed that a photon's energy is related to its frequency.
E = hv
In this equation, h is a constant known as Planck's constant, which is equal to 6.626 x 10-34 J-s.
Calculate the energy of a single photon of red light with a wavelength of 700.0 nm and a mole of these photons as an example.
The frequency of red light with a wavelength of 700.0 nm is 4.283 x 1014 s-1. When this frequency is substituted into the Planck-Einstein equation, the following conclusion is obtained.
E = ( 6.626 × 10-34 J-s)( 4.283 × 1014s-1) = 2.838 × 10-19 J
A single photon of red light carries an insignificant amount of energy. But a mole of these photons carries about 171,000 joules of energy, or 171 kJ/mol.
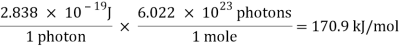
A mole of red light absorbed would thus give enough energy to raise the temperature of a litre of water by more than 40 degrees Celsius.
Because hydrogen atoms can only produce or absorb radiation at a restricted number of frequencies, they can only absorb radiation with a restricted range of energies. This indicates that the hydrogen atom contains a finite number of energy levels. These energy levels can be measured. The hydrogen atom's energy levels are quantized.
Q12) Rutherford's Scattering Experiment and Explain Its Observations.
A12)
Rutherford's model of an atom:
Ernest Rutherford was fascinated by the arrangement of electrons within an atom. For this, Rutherford devised an experiment. Fast moving alpha ()-particles were created to fall on a thin gold foil in this experiment.
- He used gold foil because he wanted the layer to be as thin as possible. The thickness of this gold foil was around 1000 atoms.
- -particles are helium ions with two charges. The fast-moving -particles have a lot of energy since they have a mass of four.
- The sub-atomic particles in gold atoms were expected to deflect -particles. He didn't anticipate to detect substantial deflections because the -particles were much heavier than the protons. The -particle scattering experiment, on the other hand, yielded completely unexpected findings.
Observations of Rutherford's scattering experiment:
As we can see in Fig.
- Most of the fast moving α-particles passed straight through the gold foil.
- Some of the α-particles were deflected by the foil by small angles.
- Surprisingly one out of every 12,000 alpha particles appeared to rebound.

Q13) Short note on Rutherford atomic model.
A13)
The atom, according to physicist Ernest Rutherford, is a miniature solar system with electrons orbiting a heavy nucleus and essentially empty space, with the nucleus occupying only a small proportion of the atom. When Rutherford suggested his concept, which featured a nucleus made entirely of protons, the neutron had not yet been identified.
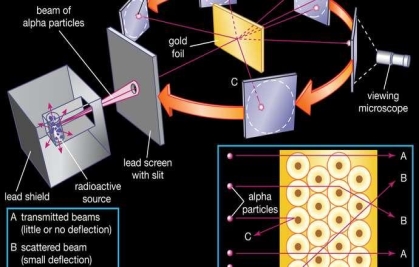
To account for the scattering of alpha particles from thin gold foil reported in a series of experiments conducted by undergraduate Ernest Marsden under the direction of Rutherford and German scientist Hans Geiger in 1909, the nucleus was proposed as small and dense. Within a protective lead shield, a radioactive source generating alpha particles (positively charged particles equivalent to the helium atom nucleus and 7,000 times more heavy than electrons) was contained. After passing through a slit in a lead screen, the radiation was focussed into a narrow beam. To detect alpha particles, a thin section of gold foil was placed in front of the slit, and a screen coated with zinc sulphide to make it luminous acted as a counter. Each alpha particle created a scintillation when it hit the fluorescent screen, which was seen through a viewing microscope mounted to the rear of the screen. Rutherford and his colleagues were able to move the screen around to see if any alpha particles were being deflected by the gold foil.
Q14) Short note on Bohr’s Model of the Hydrogen Atom.
A14)
In terms of atomic structure, Bohr's model of the hydrogen atom is the first to correctly explain the radiation spectra of atomic hydrogen. The model holds a unique place in physics history since it introduced an early quantum theory, which sparked new scientific thought and eventually led to the development of quantum mechanics. To grasp the details of Bohr's model, it's necessary to first review the nineteenth-century discoveries that led to its creation.
Using a prism to investigate white light from the sun, we may see various dark lines in the solar spectrum ((Figure)). Fraunhofer lines are named after Joseph von Fraunhofer, who properly calculated the wavelengths of solar absorption lines. Gustav Kirchhoff and Robert Bunsen found that the line emission spectra of a chemical element exactly matches its line absorption spectrum between 1854 and 1861. The distinction between the absorption and emission spectra is described in (Figure). When light passes through a gas, it produces an absorption spectrum. On the background of the continuous spectrum of white light, this spectrum appears as black lines that only exist at certain wavelengths ((Figure)). The wavelengths that are lacking indicate which wavelengths of radiation are absorbed by the gas. When a gas emits light, the emission spectrum is detected. Colorful lines on a dark backdrop represent the spectrum (see (Figure) and (Figure)). The positions of the emission lines reveal the wavelengths of radiation the gas emits. Each chemical element emits a distinct spectrum of light. The positions of each element's emission lines are identical to the positions of its absorption lines. This means that atoms of a certain element absorb only specified wavelengths of radiation, and that radiation that does not have these wavelengths is not absorbed at all. This also means that the wavelengths of the radiation emitted by each element's atoms are identical to the wavelengths of the energy they absorb.
In the solar emission spectrum in the visible range from 380 nm to 710 nm, Fraunhofer lines are observed as vertical black lines at specific spectral positions in the continuous spectrum. Thousands of similar lines are detected by highly sensitive contemporary devices.
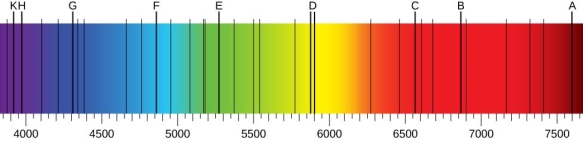
Line spectra observation: (a) absorption lines are observed; (b) emission lines are observed. (a) White light travels through a glass flask containing a chilly gas. The wavelengths of the passing light are separated using a prism. Some wavelengths in the spectrum of the passing light are missing, resulting in black absorption lines in the continuous spectrum on the viewing screen. (b) A gas is held in a glass discharge tube with electrodes on both ends. The gas glows when there is a large potential difference between the electrodes, and the light it emits passes through the prism that separates its wavelengths. Only specified wavelengths are present in the emitted light's spectrum, which are visible on the screen as multicoloured emission lines.
Q15) Give Introduction to Atomic Spectroscopy.
A15)

Fig. Energy Transitions
Atomic spectroscopy is the study of an element's electromagnetic or mass spectrum to determine its composition. Optical Atomic Spectroscopy is the study of an element's electromagnetic spectrum. Within an atom, electrons exist in different energy states. Electrons travelling between these levels must absorb or emit energy equal to the difference in their energies. The energy absorbed to shift an electron to a higher energetic energy level and/or the energy emitted as the electron goes to a less energetic energy level is measured in photons in optical spectroscopy. The electronic transition that has happened is closely related to the wavelength of the emitted radiant radiation. The wavelength of light emitted is a unique attribute of each individual element because each has its own electrical structure. Because a large atom's orbital structure can be complicated, several electronic transitions can occur, each of which results in the emission of a specific wavelength of light, as seen below.

How the three techniques are implemented.
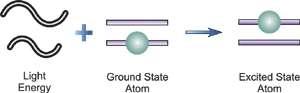
Three analytical approaches have emerged from the study of atomic spectroscopy: Atomic Absorption is a term that refers to the process of absorbing Emission of atoms. Fluorescence of atoms. In all three domains of atomic spectroscopy, the process of excitation and decay to the ground state is involved. The energy received in the excitation process or the energy emitted in the decay process is measured and analysed.
When a free, ground state atom is struck by light of just the correct wavelength, the atom may absorb the light as it transitions to an excited state, a process known as atomic absorption. On the right, you can see how this works. The amount of light at the resonant wavelength that is absorbed as it travels through a cloud of atoms is referred to as atomic absorption. The amount of light absorbed grows in a predictable manner as the number of atoms in the light path rises. A quantitative determination of the amount of analyte element present can be made by measuring the amount of light absorbed. Individual elements can be determined quantitatively in the presence of others using special light sources and careful wavelength selection. Providing enough heat energy to the sample to breakdown the chemical compounds into free atoms produces the atom cloud required for atomic absorption measurements. This is accomplished by aspirating a sample solution into a flame aligned with the light beam. Most atoms will remain in the ground state at the right flame conditions and will be able to absorb light at the analytical wavelength from a source lamp. Because of the ease and speed with which precise and accurate assessments can be produced, atomic absorption has become one of the most preferred methods for determining metals.
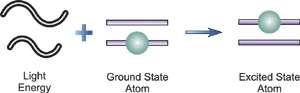
The atomic absorption process
A sample is exposed to a high-energy, thermal environment in order to develop excited state atoms capable of producing light in atomic emission. An electrical arc, a flame, or, more recently, a plasma can all be used as energy sources. Because of the discrete nature of the emitted wavelengths, the emission spectrum of an element exposed to such an energy source consists of a collection of the permissible emission wavelengths, generally referred to as emission lines. This emission spectrum can be used to qualitatively identify an element by its emission spectrum. In qualitative analysis, atomic emission utilising electrical arcs has been widely employed. Emission techniques can also be used to figure out how much of a particular element is in a sample. The intensity of light emitted at the wavelength of the element to be evaluated is measured for a "quantitative" analysis. As the number of atoms in the analyte element rises, the emission intensity at this wavelength increases. Flame photometry is a technology that uses atomic emission to do quantitative analysis.
Q16) Explain Bohr correspondence principle.
A16)
Despite the prominence of this interpretation in the physics literature, current Bohr scholars agree that Bohr did not mean his correspondence principle to indicate some form of general necessity that quantum mechanics retrieve the predictions of classical mechanics in the classical limit (see Section 6). There is less agreement, however, on which relationship between classical and quantum mechanics Bohr meant the correspondence principle to designate. In the literature, there are three main contenders, all of which are supported by Bohr's publications. The frequency interpretation, the intensity interpretation, and the selection rule interpretation are the three interpretations that can be labelled.
The correspondence principle is characterised by the frequency interpretation as a statistical asymptotic agreement between the (quantum) frequency, vn′Vn", of radiation released in a quantum leap of difference from state n′ to n′′ and the (classical) frequency () in the n′ stationary state, namely
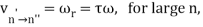
Where, n′−n′′=τ
It's worth noting that this equality between the quantum frequency and one component of the classical frequency applies only in the case of large quantum numbers—it doesn't hold for low quantum-number transitions. Furthermore, there is only statistical agreement because classically all the frequencies will be given off together, whereas quantum mechanically only a single photon with a single frequency is emitted in any given transition between stationary states; thus, one must compare the classical spectrum with a statistical ensemble of atoms.
The correspondence principle, according to the intensity interpretation, is described as the agreement, in the limit of large quantum numbers, between the probability, Pn′n", of a transition between two stationary states separated by and the square of the amplitude, C, of the classical motion:
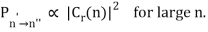
Thus in the limit of large nn the amplitudes of the harmonic components of the electron’s classical orbit can be used to calculate the intensities of the spectral lines. While the amplitude of radiation determines its intensity in classical physics, the number of photons released at a given frequency determines the intensity of a spectral line in quantum physics. As a result, the more likely a quantum transition is, the more photons will be emitted, and the higher the intensity. It's worth noting that, like the frequency interpretation, this is merely a statistical relationship that holds only in the case of big quantum numbers.
Bohr's correspondence principle is best understood as the assertion that each permissible quantum transition between stationary states corresponds to one harmonic component of classical motion, according to the selection rule interpretation. More precisely, Bohr’s selection rule states that the transition from a stationary state n′ to another stationary state n′′ is allowed if and only if there exists a τth harmonic in the classical motion of the electron in the initial stationary state; if there is no τth harmonic in the classical motion, then transitions between stationary states whose separation is τ are not allowed quantum mechanically. Figure 1 depicts the essence of Bohr's correspondence principle.
Q17) Explain Frank hertz experiment.
A17)
The hydrogen atom's Bohr model was effective in that it accurately explained the spectrum of radiation emitted by these atoms. In essence, the model suggested the presence of discrete electronic energy levels in atoms, which could be estimated based on the assumption that the circling electrons' angular momentum was quantized. The spectrum of atomic hydrogen was explained using a combination of the concept of quantized energy levels and the idea that a quanta of radiation can only be released (with frequency determined by the Einstein relation) when an atom shifts its energy to a more tightly bound state. Other methods of obtaining more direct proof of the existence of distinct energy levels in atomic systems exist, though. The effect of hitting mercury atoms with electrons will be investigated in this experiment. Because atoms are thought to have discrete energy levels, one would anticipate energy to be transferred to the atom in distinct amounts after collisions with electrons. Inelastic scattering is one proposed process, in which a defined quantity of transmitted electron energy is absorbed by the entire atom, raising it to an excited state. The mechanics of such a collision allow the atomic system to absorb practically all of the energy of the input electron, as long as the atom does not become ionised. In 1914, Franck and Hertz attempted to validate these notions for the first time. Specifically, that atomic systems contain discrete energy levels that can be stimulated by bombardment electron collisions, and that the energy differences between the levels correspond to spectroscopic measurements. Using mercury vapour, we will perform the Franck-Hertz experiment. The wavelength of the spectral line detected in mercury discharges, which corresponds to the energy levels we will detect, is 2537. There are many additional lines in the mercury spectra, but using a Franck-Hertz setup, it is extremely difficult to excite these energy differences in the mercury atom.
Q18) What Equipment used in Frank hertz experiment.
A18)
Figure 1 shows a diagram of the equipment that will be used. It consists of a thermionic tube with a cathode, an anode, and a collector or counter electrode as the third electrode. A little blob of mercury is also present in the tube. The tube is grounded by the metal case that surrounds it. To keep a mercury vapour pressure in the tube, the mercury is heated to 180 degrees Celsius. Of course, pressure varies with temperature, and the amount of pressure is crucial to the experiment. There may be too few mercury atoms to create noticeable effects if the vapour density is too low. When the pressure is too high, the mean free path is reduced, and thermal agitation occurs.

In relation to the cathode, the anode is connected to a variable voltage source (0 to +50 Volts). In relation to the anode, the counter electrode is kept at a voltage of 0.5 to 1.5 volts negative. A voltage divider and a 1.5 volt battery can be used to control the counter electrode voltage.
The cathode-anode system essentially functions as a diode. Some electrons can travel through the anode, which is a grid-like structure, and overcome the 0.5 - 1.5 Volts retarding potential to reach the counter electrode if they are energetic enough. The Keithley Electrometer, which is a very sensitive device capable of measuring the little current involved, can be used to measure the counter current.
However, we must evaluate how the presence of mercury vapour alters the system's behaviour. The mercury atoms will collide with electrons propelled from the cathode to the anode. When electrons gain enough energy to inelastically excite a mercury atom, they can lose the majority of their energy. It may therefore be unable to overcome the 0.5 - 1.5 Volts required to reach the counter electrode due to a lack of energy. As the anode voltage is increased, the counter current should drop sharply at the energy level where such collisions can occur. The counter current begins to grow again at greater voltages, but the electrons eventually accumulate enough energy to experience two or more inelastic collisions. As a result, the observed current-voltage curve should be continuously rising with a sequence of dips; the difference in energy between the ground state and first excited state in the mercury atoms will correspond to the interval of two dips.
Q19) Short note on Data Analysis in Frank hertz experiment.
A19)
For each data set, graph current vs. Voltage.
- Calculate the amount of energy transferred from an electron to a mercury atom in an inelastic collision using your graphs.
- Compare this to the projected energy from the spectral line 2537. Estimate Planck's constant using the energy given above and the 2537 spectral line (with associated uncertainty).
- To extract an electron from a metal, a specific minimum energy is required; this is referred to as the metal's "work function." The anode's work function is higher than the cathode's, resulting in a "contact-potential differential" between the anode and the cathode. It causes the entire Current vs. Voltage curve to change (why?). Calculate the difference in contact potential.
- Describe the characteristics of the detected counter current. Temperature, vapour pressure, accelerating voltage, space charge, and other physical events influence these characteristics. Make sure to bring these up in your conversation. One of the references given below may be of assistance to you.
Q20) Short note on Sommerfeld atom model.
A20)
Sommerfeld made two major changes to Bohr's theory in order to explain the observed fine structure of spectral lines.
I According to Sommerfeld, an electron's route around the nucleus is a general ellipse with the nucleus as one of its foci.
(ii) The electron's velocity in an elliptical orbit change at different points along the orbit. The mass of the travelling electron varies relativistically as a result of this.
When elliptical orbits are allowed, there are now two variables to consider.
(i) The electron's fluctuating distance from the nucleus (r).
(ii) The azimuthal angle, which describes the changing angular location of the electron with regard to the nucleus (Fig).
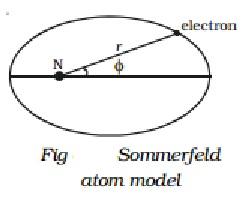
Two quantum numbers are introduced to cope with these two variables.
(i) In Bohr's theory, the primary quantum number n governs the energy of the electrons, and
(ii) an orbital (or azimuthal) quantum number (l) that has been introduced to characterise the angular momentum in an orbit, i.e., it determines the electron's orbital angular momentum. Its values range from zero to (n-1) in unity steps.
This orbital quantum number (l) can be used to calculate the number of potential elliptical orbits. The elliptical orbits that are possible are such that
b/a = l+1/n
Where a and b are the ellipse's semi-major and semi-minor axes, respectively.
Sommerfeld's model states that for any principal quantum number n, there are n potential sub-orbits or sub-shells with various eccentricities. One of the n subshells is circular, whereas the others (i.e., n-1) are elliptical
Because of the relativistic difference in electron mass, these hypothetical sub-orbits have slightly different energies
Unit - 1
Atomic Spectra and Models
Q1) Explain Inadequacy of classical physics.
A1)
The explanation of classical physics: When an electric charge vibrates, it produces light, which is an electromagnetic wave. (The term "vibrates" refers to any change in the charge's motion, such as speeding up, slowing down, or changing direction.) Remember that heat is nothing more than the kinetic energy of random motion. Electrons vibrate in random directions in a heated object, producing light as a result. A hotter object produces more energetic vibrations, which results in more light being emitted —- it lights brighter. So far, everything has gone well. Classical physics, on the other hand, was unable to explain the form of the blackbody spectrum.
A heated object's electrons can vibrate at a variety of frequencies, from a few vibrations per second to thousands of vibrations per second. In reality, there is no limit to the frequency that can be used. According to classical physics, each vibration frequency should have the same energy. Because the frequency has no upper limit, the energy of the vibrating electrons at high frequencies has no upper limit. This indicates that, according to classical physics, the energy of light produced by electrons vibrating at high frequencies has no limit. The blackbody spectrum always becomes smaller on the left-hand side in experiments (short wavelength, high frequency).
Max Planck came up with the solution in 1900. He claimed that the traditional concept that each vibration frequency should have the same energy was incorrect. Instead, he claimed that electrons vibrating at various frequencies do not share energy evenly. Energy, according to Planck, arrives in clumps. A clump of energy was dubbed a quantum by him. The size of a clump of energy —- a quantum —- is determined by the vibration frequency. Planck's rule for a quantum of energy for a vibrating electron is as follows:
Quantum energy = (a calibration constant) x (frequency of vibration)
Or
Hf = E
The calibration constant, h, is now known as Planck's constant. It’s worth is approximately 6 x 10-34, which is quite small!
So, how does this explain the blackbody radiation spectrum? According to Planck, an electron vibrating at frequency f could only have an energy of 1 hf, 2 hf, 3 hf, 4 hf, and so on; that is, an electron vibrating at frequency f could only have an energy of 1 hf, 2 hf, 3 hf, 4 hf, and so on.
(Any integer) x hf = energy of a vibrating electron
If the electron is to vibrate, it must have at least one quantum of energy. If it doesn't have at least 1hf of energy, it won't vibrate and won't be able to create any light. Exclaimed Planck, "the amount of energy in a quantum, hf, is so great at high frequencies that the high-frequency vibrations can never get underway!" This is why the left-hand (high frequency) side of the blackbody spectrum is always narrow.
Q2) How is Radiation Absorbed?
A2)
What exactly does "black body" radiation imply? The argument is that the radiation emitted by a heated body is influenced by the body being heated to some amount. Let's take a step back for a moment and analyse how different materials absorb radiation. Some, such as glass, appear to absorb very little light and let it pass right through. A gleaming metallic surface does not absorb light; instead, it reflects it. Light and heat are almost fully absorbed by a black material like soot, and the material becomes warm. How can we explain these diverse behaviours in terms of light interacting with charges in the material, causing these charges to oscillate and absorb energy from the radiation? In the case of glass, this clearly does not occur, at least not frequently. What's to stop you? Quantum mechanics is required to fully comprehend why, but the fundamental notion is that there are charges—electrons—in glass that can oscillate in response to an applied external oscillating electric field, but these charges are strongly linked to atoms and can only oscillate at particular frequencies. (These charge oscillations occur as an electron jumps from one orbit to another, according to quantum experts.) Of course, in the 1890s, when the first precision work on black body radiation was being done, this was not understood.) Because none of these frequencies correlate to visible light in regular glass, there is no resonance with a light wave, and thus minimal energy is absorbed. As a result, glass is ideal for windows! That's a given. Glass, on the other hand, is opaque at frequencies outside the visual range (in general, both in the infrared and the ultraviolet). These are the natural oscillation frequencies of the electrical charge distributions in atoms or bonds.
How can we comprehend how a metal surface reflects light? Electrons in a piece of metal are free to move across the entire solid. This is what distinguishes a metal from other materials: it easily transmits both electricity and heat, which are conveyed by currents of freely moving electrons. (Well, vibrations do carry a small amount of heat.) Metals, on the other hand, are easily identifiable due to their lustrous appearance—why is that? Again, it's those free electrons: the electrical field of the incoming light wave drives them into enormous (compared to the atoms) oscillations, and this generated oscillating current radiates electromagnetically, exactly like a current in a transmitting antenna. The reflected light is the source of this radiation. Little of the incoming radiant energy is absorbed as heat by a polished metal surface; instead, it is reradiated, or reflected.
Consider a substance that absorbs light and does not transmit or reflect it. With soot, we're quite near to perfect absorption. It will conduct an electric current like a metal, but not nearly as effectively. Unattached electrons can flow across the entire solid, but they constantly collide with objects because they have a short mean free path. They create vibration when they bump, similar to balls hitting bumpers in a pinball machine, and hence release kinetic energy as heat. Although the electrons in soot have a shorter mean free path than those in a good metal, they travel far more freely than electrons attached to atoms (as in glass), allowing them to accelerate and absorb energy from the light wave's electric field. As a result, they are extremely efficient at converting energy from light waves to heat.
Q3) What about Equipartition of Energy?
A3)
The energy equipartition is a key conclusion of classical statistical mechanics: for a system in thermal equilibrium, each degree of freedom has an average energy of 12kBT. (Boltzmann's constant is kB.) Thus molecules in a gas have average kinetic energy 32kBT, 12kBT for each direction, and a simple one-dimensional harmonic oscillator has total energy kBT: 12kBT kinetic energy and 12kBT potential energy.
Comparing now the formula for the number of modes N(f)Δf in a small interval Δf

With Planck’s formula for radiation energy intensity in the same interval:
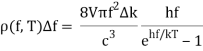
For the low frequency modes hf≪kBT we can make the approximation
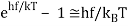
And it follows immediately that each mode has energy kBT, in line with classical predictions.
However, things go horribly wrong on a regular basis! The number of modes grows indefinitely, but the energy in these high-frequency modes decreases exponentially as the frequency rises. This was eventually termed the UV catastrophe by Ehrenfest. Rayleigh's sound strategy didn't appear to be that sound after all—something vital was lacking.
Planck never discussed equipartition, which is maybe unexpected. Of fact, as Rayleigh pointed out, equipartition was recognised to have issues, such as in the case of gas specific heat. In truth, Planck was unsure about the existence of atoms, writing subsequently that “I had been inclined to oppose atomism” in the 1890s (see notes). Even Boltzmann was unclear how successfully oscillators achieved thermal equilibrium with electromagnetic radiation—after all, it was well known that diatomic molecules oscillated with kinetic energy but did not achieve classical thermal equilibrium. (Maxwell observed that hot gases generate light at specific frequencies as early as 1877.) The oscillations must be simple harmonic because the frequencies do not change with temperature—but such an oscillator would surely be activated by collisions at low temperatures, so why wasn't energy delivered into this mode?)
Q4) Short Note on Wien’s Displacement Law.
A4)
Wien's Displacement Law is easily deduced from Planck's formula: the highest radiation per unit frequency range occurs at the frequency f for which the function f3/(ehf/kBT1) is at its maximum. Numerically, hfmax=2.82kBT is obtained.
The equation linking the frequency of maximum energy intensity in units of Joules/m3/Hz may be established theoretically (and is proven experimentally) as fmax=5.881010 T Hz/K.
The law is frequently expressed in terms of the wavelength at which the intensity, now measured in Joules/m3/m, or per unit interval of wavelength, and
2.910-3 TmK is the maximum value.
The crucial thing to remember here is that these calculations do not produce the same result, as can be easily confirmed, because fmaxmax1.7108m/sec is not the same as the speed of light! Because the two measurements, per unit interval of frequency and per unit interval of wavelength, are distinct, a claim that, for example, sunlight is most intense in the yellow must explain which one is being utilised (actually it would be wavelength, frequency would give the near infrared).
An Excel spreadsheet was used to create the graphs of black body radiation as a function of temperature. You are invited to download and experiment with this spreadsheet to see how radiation varies with temperature. It's simple to use—all you have to do is enter the temperature and see the graph change.
Q5) Explain the Applications of Photoelectric effect.
A5)
Photoelectric devices have a number of advantages, including creating a current that is precisely proportional to light intensity and having a very fast response time. The photoelectric cell, often known as a photodiode, is a simple device. This was originally a phototube, a vacuum tube with a metal cathode with a tiny work function that allowed electrons to be easily emitted. An anode held at a large positive voltage compared to the cathode would collect the current produced by the plate. Phototubes have been phased out in favour of semiconductor-based photodiodes, which can detect light, quantify its intensity, operate other devices in response to illumination, and convert light to electrical energy. These devices operate at low voltages, similar to their bandgaps, and are utilised in a variety of applications including industrial process control, pollution monitoring, light detection in fibre optic telecommunications networks, solar cells, imaging, and many more.
Semiconductors with bandgaps that correspond to the photon energy to be sensed make up photoconductive cells. Photographic exposure metres and automatic street lighting switches, for example, function in the visible spectrum and are often constructed of cadmium sulphide. Lead sulphide or mercury cadmium telluride can be used to make infrared detectors, such as night-vision sensors.
A semiconductor p-n junction is commonly used in photovoltaic devices. Solar cells are typically built of crystalline silicon and convert approximately 15% of incident light energy into electricity. Solar cells are frequently utilised in specialised contexts such as space satellites and remote telephone sites to produce very tiny amounts of power. Solar power may become economically viable for large-scale applications when cheaper materials and higher efficiency become available.
The photomultiplier tube is a very sensitive extension of the phototube, which contains a sequence of metal plates called dynodes and was first created in the 1930s. When light strikes the cathode, electrons are released. These are drawn to the first dynode, where they release more electrons, which then strike the second, and so on. The photocurrent is boosted so much after up to ten dynode stages that some photomultipliers can almost detect a single photon. In spectroscopic research, where it is frequently necessary to monitor extremely faint light sources, these devices, or solid-state counterparts of comparable sensitivity, are important. They're also employed in scintillation counters, which have a substance that creates light flashes when X-rays or gamma rays strike it, as well as a photomultiplier that counts and measures the strength of the flashes. These counters are employed for things like recognising certain isotopes for nuclear tracer analysis and detecting X-rays in computerised axial tomography (CAT) scans, which show a cross section of the body.
Q6) What is Compton Effect? Explain its Derivation.
A6)
The Compton effect is the phenomenon that occurs when x-rays or gamma rays are scattered on a substance with increasing wavelength. In the year 1922, Arthur Compton investigated this phenomenon. Compton discovered that wavelength is unaffected by incident radiation intensity during his research. It is determined by the scattering angle as well as the wavelength of the incident beam. It is expressed mathematically as follows:
What is the location?
The angle at which light is scattered
m0: an electron's rest mass
h/m0c : The electron's Compton wavelength
The peaks of the radiation spectrum are denoted by the letters s and 0.
Derivation of Compton effect equation
Considering the elastic collide between a photon and an electron, following is the derivation:
hν0 : energy of photon
Pi=hν0/c :momentum of the photon
Pi=pfcosΘ+pecosϕ(1) (conservation of momentum in x direction)
0=−pfsinΘ+pesinϕ(2) (conservation of momentum in y direction)


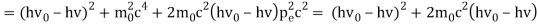
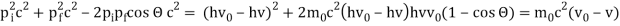
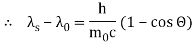
Therefore, above is the Compton effect equation andhm0c≡λc is Compton wavelength of an electron.
Q7) Difference Between Compton Effect and Photoelectric Effect.
A7)
Compton effect | Photoelectric effect |
This is the result of high-energy photons being bound to free electrons dispersing inelastically. | When electromagnetic radiation interacts with electrons, weakly bound electrons are expelled from the surface of the material, causing this effect. |
The effect was explained by Arthur Compton. | The effect was explained by Albert Einstein. |
The free electrons have a mid-energy level of energy. | The electrons have a low-energy associated with them. |
The dispersed photon has a longer wavelength than the incident photon. | The photon vanishes after interacting with the electrons, therefore the wavelength isn't visible. |
Q8) What is Wave-Particle Duality: Light?
A8)
Does light consist of particles or waves? When one focuses upon the different types of phenomena observed with light, a strong case can be built for a wave picture:


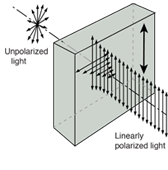
Fig. Interference Diffraction Polarization
Phenomenon | Can be explained in | Can be explained in |
Reflection |  |  |
Refraction |  |  |
Interference |  |  |
Diffraction |  |  |
Polarization |  |  |
Photoelectric effect |  |  |
Waves can explain the majority of regularly observed light phenomena. However, the photoelectric effect suggested that light has a particle nature. Then electrons were discovered to have multiple natures as well.
There is a lot of debate in the literature concerning whether light reflection and refraction can be represented in particle terms at an interface when the medium changes. Treating light as a wave phenomenon is sufficient for practical geometrical optics applications.
Q9) Define Atomic spectra and Explain Spectral Series of Hydrogen Atom.
A9)
An electron's spectrum of electromagnetic radiation released or absorbed as it moves between different energy levels within an atom.
When an electron moves from one energy level to the next, it emits or absorbs light of a given wavelength. The atomic spectra of atoms is the collection of all these unique wavelengths of the atom in a certain set of variables such as pressure, temperature, and so on. Emission spectra, absorption spectra, and continuous spectra are the three forms of atomic spectra.
Spectral Series of Hydrogen Atom
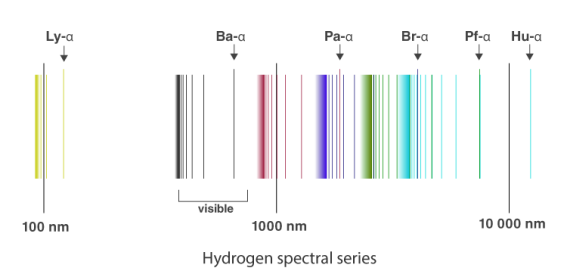
The atomic hydrogen emission spectrum is divided into a number of spectral lines with wavelengths determined by the Rydberg formula, as seen in the image above. The atomic transitions between different energy levels cause the observed spectral lines in the hydrogen emission spectrum. In astronomical spectroscopy, spectral series are crucial.
Q10) What is Hydrogen spectrum?
A10)
The hydrogen spectrum is a crucial piece of evidence for demonstrating an atom's quantized electronic structure. When an electric discharge is conducted across a gaseous hydrogen molecule, the hydrogen atoms in the molecule dissociate. The energetically excited hydrogen atoms emit electromagnetic radiation as a result of this process. The hydrogen emission spectrum is made up of discrete frequency radiation. These radiation series bear the names of the scientists who discovered them.
The spectral lines of the hydrogen atomic emission spectrum are explained by Bohr's hypothesis. The energy of an atom's electron remains unaltered while it is in the ground state. The electron jumps from the ground state orbit to a more distant excited state orbit when the atom absorbs one or more quanta of energy. The variable n is used to identify energy levels. n = 1 is the ground state, n = 2 is the first excited state, and so on. The difference in energy between the two energy levels is equal to the energy obtained by the atom. When the atom relaxes back to a lower energy state, energy equal to the difference in energy between the two orbits is released (see Figure 1).
According to the equation E = hv, the change in energy, E, causes light of a specific frequency to be emitted. Remember that the atomic emission spectrum of hydrogen has four different frequency spectral lines? The finding that electron orbits are not evenly spaced is explained in the Bohr model. The spacing between the levels gets narrower and smaller as the energy travels further away from the nucleus.
Bohr was able to calculate the energies that the hydrogen electron would have in each of its permissible energy levels using the wavelengths of the spectral lines. The energy level transitions that corresponded to the spectral lines in the atomic emission spectrum were then mathematically demonstrated ( Figure 2).
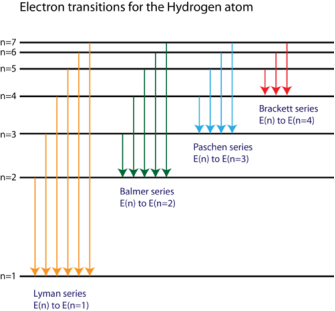
Figure. The electron energy level diagram for the hydrogen atom.
Q11) Give Explanation of the Emission Spectrum.
A11)
A theoretical explanation of the spectrum of radiation released by a glowing object was offered by Max Planck. He proposed that the walls of a glowing solid may be visualised as a set of resonators oscillating at various frequencies. These resonators absorb energy from the object's walls in the form of heat and release it in the form of electromagnetic radiation. At any given time, the energy of these resonators is proportional to the frequency with which they vibrate.
Planck had to postulate that the energy of these oscillators could only take on a restricted number of values in order to suit the observed spectrum. To put it another way, the energy spectrum for these oscillators was no longer continuous. These oscillators are theoretically "countable" since the number of possible energy levels is restricted. As a result, the energy of the oscillators in this system is quantized. To explain how light was emitted, Planck created the concept of quantization.
Planck's work was extended by Albert Einstein to include the light that had been emitted. Einstein proposed that light acted like a stream of little bundles, or packets, of energy, at a time when everyone accepted that light was a wave (and thus continuous). To put it another way, light was quantized as well. Einstein's model was predicated on two premises. To begin, he assumed that light was made up of photons, which are small, distinct energy bundles. He also assumed that a photon's energy is related to its frequency.
E = hv
In this equation, h is a constant known as Planck's constant, which is equal to 6.626 x 10-34 J-s.
Calculate the energy of a single photon of red light with a wavelength of 700.0 nm and a mole of these photons as an example.
The frequency of red light with a wavelength of 700.0 nm is 4.283 x 1014 s-1. When this frequency is substituted into the Planck-Einstein equation, the following conclusion is obtained.
E = ( 6.626 × 10-34 J-s)( 4.283 × 1014s-1) = 2.838 × 10-19 J
A single photon of red light carries an insignificant amount of energy. But a mole of these photons carries about 171,000 joules of energy, or 171 kJ/mol.
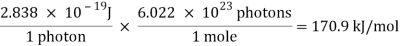
A mole of red light absorbed would thus give enough energy to raise the temperature of a litre of water by more than 40 degrees Celsius.
Because hydrogen atoms can only produce or absorb radiation at a restricted number of frequencies, they can only absorb radiation with a restricted range of energies. This indicates that the hydrogen atom contains a finite number of energy levels. These energy levels can be measured. The hydrogen atom's energy levels are quantized.
Q12) Rutherford's Scattering Experiment and Explain Its Observations.
A12)
Rutherford's model of an atom:
Ernest Rutherford was fascinated by the arrangement of electrons within an atom. For this, Rutherford devised an experiment. Fast moving alpha ()-particles were created to fall on a thin gold foil in this experiment.
- He used gold foil because he wanted the layer to be as thin as possible. The thickness of this gold foil was around 1000 atoms.
- -particles are helium ions with two charges. The fast-moving -particles have a lot of energy since they have a mass of four.
- The sub-atomic particles in gold atoms were expected to deflect -particles. He didn't anticipate to detect substantial deflections because the -particles were much heavier than the protons. The -particle scattering experiment, on the other hand, yielded completely unexpected findings.
Observations of Rutherford's scattering experiment:
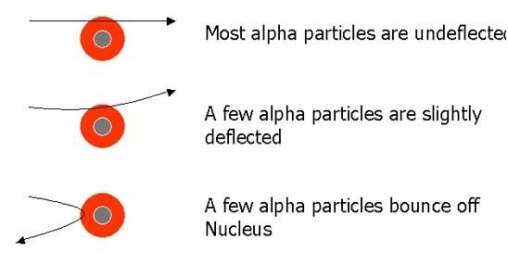
As we can see in Fig.
- Most of the fast moving α-particles passed straight through the gold foil.
- Some of the α-particles were deflected by the foil by small angles.
- Surprisingly one out of every 12,000 alpha particles appeared to rebound.
Q13) Short note on Rutherford atomic model.
A13)
The atom, according to physicist Ernest Rutherford, is a miniature solar system with electrons orbiting a heavy nucleus and essentially empty space, with the nucleus occupying only a small proportion of the atom. When Rutherford suggested his concept, which featured a nucleus made entirely of protons, the neutron had not yet been identified.
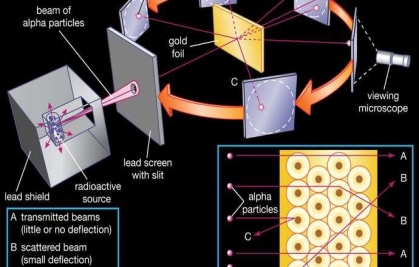
To account for the scattering of alpha particles from thin gold foil reported in a series of experiments conducted by undergraduate Ernest Marsden under the direction of Rutherford and German scientist Hans Geiger in 1909, the nucleus was proposed as small and dense. Within a protective lead shield, a radioactive source generating alpha particles (positively charged particles equivalent to the helium atom nucleus and 7,000 times more heavy than electrons) was contained. After passing through a slit in a lead screen, the radiation was focussed into a narrow beam. To detect alpha particles, a thin section of gold foil was placed in front of the slit, and a screen coated with zinc sulphide to make it luminous acted as a counter. Each alpha particle created a scintillation when it hit the fluorescent screen, which was seen through a viewing microscope mounted to the rear of the screen. Rutherford and his colleagues were able to move the screen around to see if any alpha particles were being deflected by the gold foil.
Q14) Short note on Bohr’s Model of the Hydrogen Atom.
A14)
In terms of atomic structure, Bohr's model of the hydrogen atom is the first to correctly explain the radiation spectra of atomic hydrogen. The model holds a unique place in physics history since it introduced an early quantum theory, which sparked new scientific thought and eventually led to the development of quantum mechanics. To grasp the details of Bohr's model, it's necessary to first review the nineteenth-century discoveries that led to its creation.
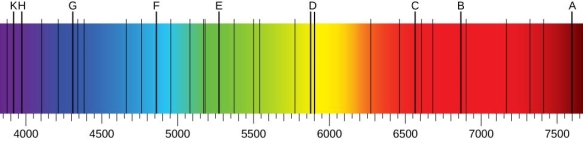
Using a prism to investigate white light from the sun, we may see various dark lines in the solar spectrum ((Figure)). Fraunhofer lines are named after Joseph von Fraunhofer, who properly calculated the wavelengths of solar absorption lines. Gustav Kirchhoff and Robert Bunsen found that the line emission spectra of a chemical element exactly matches its line absorption spectrum between 1854 and 1861. The distinction between the absorption and emission spectra is described in (Figure). When light passes through a gas, it produces an absorption spectrum. On the background of the continuous spectrum of white light, this spectrum appears as black lines that only exist at certain wavelengths ((Figure)). The wavelengths that are lacking indicate which wavelengths of radiation are absorbed by the gas. When a gas emits light, the emission spectrum is detected. Colorful lines on a dark backdrop represent the spectrum (see (Figure) and (Figure)). The positions of the emission lines reveal the wavelengths of radiation the gas emits. Each chemical element emits a distinct spectrum of light. The positions of each element's emission lines are identical to the positions of its absorption lines. This means that atoms of a certain element absorb only specified wavelengths of radiation, and that radiation that does not have these wavelengths is not absorbed at all. This also means that the wavelengths of the radiation emitted by each element's atoms are identical to the wavelengths of the energy they absorb.
In the solar emission spectrum in the visible range from 380 nm to 710 nm, Fraunhofer lines are observed as vertical black lines at specific spectral positions in the continuous spectrum. Thousands of similar lines are detected by highly sensitive contemporary devices.
Line spectra observation: (a) absorption lines are observed; (b) emission lines are observed. (a) White light travels through a glass flask containing a chilly gas. The wavelengths of the passing light are separated using a prism. Some wavelengths in the spectrum of the passing light are missing, resulting in black absorption lines in the continuous spectrum on the viewing screen. (b) A gas is held in a glass discharge tube with electrodes on both ends. The gas glows when there is a large potential difference between the electrodes, and the light it emits passes through the prism that separates its wavelengths. Only specified wavelengths are present in the emitted light's spectrum, which are visible on the screen as multicoloured emission lines.
Q15) Give Introduction to Atomic Spectroscopy.
A15)

Fig. Energy Transitions
Atomic spectroscopy is the study of an element's electromagnetic or mass spectrum to determine its composition. Optical Atomic Spectroscopy is the study of an element's electromagnetic spectrum. Within an atom, electrons exist in different energy states. Electrons travelling between these levels must absorb or emit energy equal to the difference in their energies. The energy absorbed to shift an electron to a higher energetic energy level and/or the energy emitted as the electron goes to a less energetic energy level is measured in photons in optical spectroscopy. The electronic transition that has happened is closely related to the wavelength of the emitted radiant radiation. The wavelength of light emitted is a unique attribute of each individual element because each has its own electrical structure. Because a large atom's orbital structure can be complicated, several electronic transitions can occur, each of which results in the emission of a specific wavelength of light, as seen below.
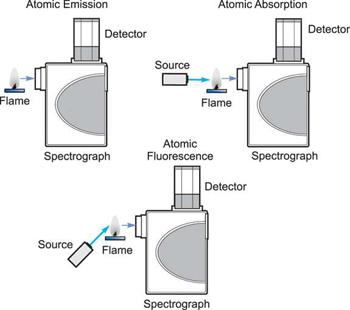
How the three techniques are implemented.
Three analytical approaches have emerged from the study of atomic spectroscopy: Atomic Absorption is a term that refers to the process of absorbing Emission of atoms. Fluorescence of atoms. In all three domains of atomic spectroscopy, the process of excitation and decay to the ground state is involved. The energy received in the excitation process or the energy emitted in the decay process is measured and analysed.
When a free, ground state atom is struck by light of just the correct wavelength, the atom may absorb the light as it transitions to an excited state, a process known as atomic absorption. On the right, you can see how this works. The amount of light at the resonant wavelength that is absorbed as it travels through a cloud of atoms is referred to as atomic absorption. The amount of light absorbed grows in a predictable manner as the number of atoms in the light path rises. A quantitative determination of the amount of analyte element present can be made by measuring the amount of light absorbed. Individual elements can be determined quantitatively in the presence of others using special light sources and careful wavelength selection. Providing enough heat energy to the sample to breakdown the chemical compounds into free atoms produces the atom cloud required for atomic absorption measurements. This is accomplished by aspirating a sample solution into a flame aligned with the light beam. Most atoms will remain in the ground state at the right flame conditions and will be able to absorb light at the analytical wavelength from a source lamp. Because of the ease and speed with which precise and accurate assessments can be produced, atomic absorption has become one of the most preferred methods for determining metals.
The atomic absorption process
A sample is exposed to a high-energy, thermal environment in order to develop excited state atoms capable of producing light in atomic emission. An electrical arc, a flame, or, more recently, a plasma can all be used as energy sources. Because of the discrete nature of the emitted wavelengths, the emission spectrum of an element exposed to such an energy source consists of a collection of the permissible emission wavelengths, generally referred to as emission lines. This emission spectrum can be used to qualitatively identify an element by its emission spectrum. In qualitative analysis, atomic emission utilising electrical arcs has been widely employed. Emission techniques can also be used to figure out how much of a particular element is in a sample. The intensity of light emitted at the wavelength of the element to be evaluated is measured for a "quantitative" analysis. As the number of atoms in the analyte element rises, the emission intensity at this wavelength increases. Flame photometry is a technology that uses atomic emission to do quantitative analysis.
Q16) Explain Bohr correspondence principle.
A16)
Despite the prominence of this interpretation in the physics literature, current Bohr scholars agree that Bohr did not mean his correspondence principle to indicate some form of general necessity that quantum mechanics retrieve the predictions of classical mechanics in the classical limit (see Section 6). There is less agreement, however, on which relationship between classical and quantum mechanics Bohr meant the correspondence principle to designate. In the literature, there are three main contenders, all of which are supported by Bohr's publications. The frequency interpretation, the intensity interpretation, and the selection rule interpretation are the three interpretations that can be labelled.
The correspondence principle is characterised by the frequency interpretation as a statistical asymptotic agreement between the (quantum) frequency, vn′Vn", of radiation released in a quantum leap of difference from state n′ to n′′ and the (classical) frequency () in the n′ stationary state, namely
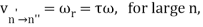
Where, n′−n′′=τ
It's worth noting that this equality between the quantum frequency and one component of the classical frequency applies only in the case of large quantum numbers—it doesn't hold for low quantum-number transitions. Furthermore, there is only statistical agreement because classically all the frequencies will be given off together, whereas quantum mechanically only a single photon with a single frequency is emitted in any given transition between stationary states; thus, one must compare the classical spectrum with a statistical ensemble of atoms.
The correspondence principle, according to the intensity interpretation, is described as the agreement, in the limit of large quantum numbers, between the probability, Pn′n", of a transition between two stationary states separated by and the square of the amplitude, C, of the classical motion:
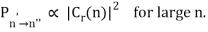
Thus in the limit of large nn the amplitudes of the harmonic components of the electron’s classical orbit can be used to calculate the intensities of the spectral lines. While the amplitude of radiation determines its intensity in classical physics, the number of photons released at a given frequency determines the intensity of a spectral line in quantum physics. As a result, the more likely a quantum transition is, the more photons will be emitted, and the higher the intensity. It's worth noting that, like the frequency interpretation, this is merely a statistical relationship that holds only in the case of big quantum numbers.
Bohr's correspondence principle is best understood as the assertion that each permissible quantum transition between stationary states corresponds to one harmonic component of classical motion, according to the selection rule interpretation. More precisely, Bohr’s selection rule states that the transition from a stationary state n′ to another stationary state n′′ is allowed if and only if there exists a τth harmonic in the classical motion of the electron in the initial stationary state; if there is no τth harmonic in the classical motion, then transitions between stationary states whose separation is τ are not allowed quantum mechanically. Figure 1 depicts the essence of Bohr's correspondence principle.
Q17) Explain Frank hertz experiment.
A17)
The hydrogen atom's Bohr model was effective in that it accurately explained the spectrum of radiation emitted by these atoms. In essence, the model suggested the presence of discrete electronic energy levels in atoms, which could be estimated based on the assumption that the circling electrons' angular momentum was quantized. The spectrum of atomic hydrogen was explained using a combination of the concept of quantized energy levels and the idea that a quanta of radiation can only be released (with frequency determined by the Einstein relation) when an atom shifts its energy to a more tightly bound state. Other methods of obtaining more direct proof of the existence of distinct energy levels in atomic systems exist, though. The effect of hitting mercury atoms with electrons will be investigated in this experiment. Because atoms are thought to have discrete energy levels, one would anticipate energy to be transferred to the atom in distinct amounts after collisions with electrons. Inelastic scattering is one proposed process, in which a defined quantity of transmitted electron energy is absorbed by the entire atom, raising it to an excited state. The mechanics of such a collision allow the atomic system to absorb practically all of the energy of the input electron, as long as the atom does not become ionised. In 1914, Franck and Hertz attempted to validate these notions for the first time. Specifically, that atomic systems contain discrete energy levels that can be stimulated by bombardment electron collisions, and that the energy differences between the levels correspond to spectroscopic measurements. Using mercury vapour, we will perform the Franck-Hertz experiment. The wavelength of the spectral line detected in mercury discharges, which corresponds to the energy levels we will detect, is 2537. There are many additional lines in the mercury spectra, but using a Franck-Hertz setup, it is extremely difficult to excite these energy differences in the mercury atom.
Q18) What Equipment used in Frank hertz experiment.
A18)
Figure 1 shows a diagram of the equipment that will be used. It consists of a thermionic tube with a cathode, an anode, and a collector or counter electrode as the third electrode. A little blob of mercury is also present in the tube. The tube is grounded by the metal case that surrounds it. To keep a mercury vapour pressure in the tube, the mercury is heated to 180 degrees Celsius. Of course, pressure varies with temperature, and the amount of pressure is crucial to the experiment. There may be too few mercury atoms to create noticeable effects if the vapour density is too low. When the pressure is too high, the mean free path is reduced, and thermal agitation occurs.
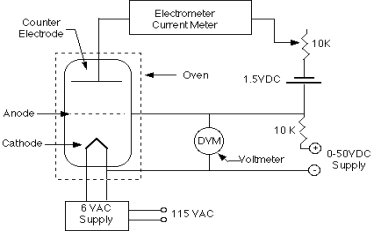
In relation to the cathode, the anode is connected to a variable voltage source (0 to +50 Volts). In relation to the anode, the counter electrode is kept at a voltage of 0.5 to 1.5 volts negative. A voltage divider and a 1.5 volt battery can be used to control the counter electrode voltage.
The cathode-anode system essentially functions as a diode. Some electrons can travel through the anode, which is a grid-like structure, and overcome the 0.5 - 1.5 Volts retarding potential to reach the counter electrode if they are energetic enough. The Keithley Electrometer, which is a very sensitive device capable of measuring the little current involved, can be used to measure the counter current.
However, we must evaluate how the presence of mercury vapour alters the system's behaviour. The mercury atoms will collide with electrons propelled from the cathode to the anode. When electrons gain enough energy to inelastically excite a mercury atom, they can lose the majority of their energy. It may therefore be unable to overcome the 0.5 - 1.5 Volts required to reach the counter electrode due to a lack of energy. As the anode voltage is increased, the counter current should drop sharply at the energy level where such collisions can occur. The counter current begins to grow again at greater voltages, but the electrons eventually accumulate enough energy to experience two or more inelastic collisions. As a result, the observed current-voltage curve should be continuously rising with a sequence of dips; the difference in energy between the ground state and first excited state in the mercury atoms will correspond to the interval of two dips.
Q19) Short note on Data Analysis in Frank hertz experiment.
A19)
For each data set, graph current vs. Voltage.
- Calculate the amount of energy transferred from an electron to a mercury atom in an inelastic collision using your graphs.
- Compare this to the projected energy from the spectral line 2537. Estimate Planck's constant using the energy given above and the 2537 spectral line (with associated uncertainty).
- To extract an electron from a metal, a specific minimum energy is required; this is referred to as the metal's "work function." The anode's work function is higher than the cathode's, resulting in a "contact-potential differential" between the anode and the cathode. It causes the entire Current vs. Voltage curve to change (why?). Calculate the difference in contact potential.
- Describe the characteristics of the detected counter current. Temperature, vapour pressure, accelerating voltage, space charge, and other physical events influence these characteristics. Make sure to bring these up in your conversation. One of the references given below may be of assistance to you.
Q20) Short note on Sommerfeld atom model.
A20)
Sommerfeld made two major changes to Bohr's theory in order to explain the observed fine structure of spectral lines.
I According to Sommerfeld, an electron's route around the nucleus is a general ellipse with the nucleus as one of its foci.
(ii) The electron's velocity in an elliptical orbit change at different points along the orbit. The mass of the travelling electron varies relativistically as a result of this.
When elliptical orbits are allowed, there are now two variables to consider.
(i) The electron's fluctuating distance from the nucleus (r).
(ii) The azimuthal angle, which describes the changing angular location of the electron with regard to the nucleus (Fig).

Two quantum numbers are introduced to cope with these two variables.
(i) In Bohr's theory, the primary quantum number n governs the energy of the electrons, and
(ii) an orbital (or azimuthal) quantum number (l) that has been introduced to characterise the angular momentum in an orbit, i.e., it determines the electron's orbital angular momentum. Its values range from zero to (n-1) in unity steps.
This orbital quantum number (l) can be used to calculate the number of potential elliptical orbits. The elliptical orbits that are possible are such that
b/a = l+1/n
Where a and b are the ellipse's semi-major and semi-minor axes, respectively.
Sommerfeld's model states that for any principal quantum number n, there are n potential sub-orbits or sub-shells with various eccentricities. One of the n subshells is circular, whereas the others (i.e., n-1) are elliptical
Because of the relativistic difference in electron mass, these hypothetical sub-orbits have slightly different energies
Unit - 1
Atomic Spectra and Models
Q1) Explain Inadequacy of classical physics.
A1)
The explanation of classical physics: When an electric charge vibrates, it produces light, which is an electromagnetic wave. (The term "vibrates" refers to any change in the charge's motion, such as speeding up, slowing down, or changing direction.) Remember that heat is nothing more than the kinetic energy of random motion. Electrons vibrate in random directions in a heated object, producing light as a result. A hotter object produces more energetic vibrations, which results in more light being emitted —- it lights brighter. So far, everything has gone well. Classical physics, on the other hand, was unable to explain the form of the blackbody spectrum.
A heated object's electrons can vibrate at a variety of frequencies, from a few vibrations per second to thousands of vibrations per second. In reality, there is no limit to the frequency that can be used. According to classical physics, each vibration frequency should have the same energy. Because the frequency has no upper limit, the energy of the vibrating electrons at high frequencies has no upper limit. This indicates that, according to classical physics, the energy of light produced by electrons vibrating at high frequencies has no limit. The blackbody spectrum always becomes smaller on the left-hand side in experiments (short wavelength, high frequency).
Max Planck came up with the solution in 1900. He claimed that the traditional concept that each vibration frequency should have the same energy was incorrect. Instead, he claimed that electrons vibrating at various frequencies do not share energy evenly. Energy, according to Planck, arrives in clumps. A clump of energy was dubbed a quantum by him. The size of a clump of energy —- a quantum —- is determined by the vibration frequency. Planck's rule for a quantum of energy for a vibrating electron is as follows:
Quantum energy = (a calibration constant) x (frequency of vibration)
Or
Hf = E
The calibration constant, h, is now known as Planck's constant. It’s worth is approximately 6 x 10-34, which is quite small!
So, how does this explain the blackbody radiation spectrum? According to Planck, an electron vibrating at frequency f could only have an energy of 1 hf, 2 hf, 3 hf, 4 hf, and so on; that is, an electron vibrating at frequency f could only have an energy of 1 hf, 2 hf, 3 hf, 4 hf, and so on.
(Any integer) x hf = energy of a vibrating electron
If the electron is to vibrate, it must have at least one quantum of energy. If it doesn't have at least 1hf of energy, it won't vibrate and won't be able to create any light. Exclaimed Planck, "the amount of energy in a quantum, hf, is so great at high frequencies that the high-frequency vibrations can never get underway!" This is why the left-hand (high frequency) side of the blackbody spectrum is always narrow.
Q2) How is Radiation Absorbed?
A2)
What exactly does "black body" radiation imply? The argument is that the radiation emitted by a heated body is influenced by the body being heated to some amount. Let's take a step back for a moment and analyse how different materials absorb radiation. Some, such as glass, appear to absorb very little light and let it pass right through. A gleaming metallic surface does not absorb light; instead, it reflects it. Light and heat are almost fully absorbed by a black material like soot, and the material becomes warm. How can we explain these diverse behaviours in terms of light interacting with charges in the material, causing these charges to oscillate and absorb energy from the radiation? In the case of glass, this clearly does not occur, at least not frequently. What's to stop you? Quantum mechanics is required to fully comprehend why, but the fundamental notion is that there are charges—electrons—in glass that can oscillate in response to an applied external oscillating electric field, but these charges are strongly linked to atoms and can only oscillate at particular frequencies. (These charge oscillations occur as an electron jumps from one orbit to another, according to quantum experts.) Of course, in the 1890s, when the first precision work on black body radiation was being done, this was not understood.) Because none of these frequencies correlate to visible light in regular glass, there is no resonance with a light wave, and thus minimal energy is absorbed. As a result, glass is ideal for windows! That's a given. Glass, on the other hand, is opaque at frequencies outside the visual range (in general, both in the infrared and the ultraviolet). These are the natural oscillation frequencies of the electrical charge distributions in atoms or bonds.
How can we comprehend how a metal surface reflects light? Electrons in a piece of metal are free to move across the entire solid. This is what distinguishes a metal from other materials: it easily transmits both electricity and heat, which are conveyed by currents of freely moving electrons. (Well, vibrations do carry a small amount of heat.) Metals, on the other hand, are easily identifiable due to their lustrous appearance—why is that? Again, it's those free electrons: the electrical field of the incoming light wave drives them into enormous (compared to the atoms) oscillations, and this generated oscillating current radiates electromagnetically, exactly like a current in a transmitting antenna. The reflected light is the source of this radiation. Little of the incoming radiant energy is absorbed as heat by a polished metal surface; instead, it is reradiated, or reflected.
Consider a substance that absorbs light and does not transmit or reflect it. With soot, we're quite near to perfect absorption. It will conduct an electric current like a metal, but not nearly as effectively. Unattached electrons can flow across the entire solid, but they constantly collide with objects because they have a short mean free path. They create vibration when they bump, similar to balls hitting bumpers in a pinball machine, and hence release kinetic energy as heat. Although the electrons in soot have a shorter mean free path than those in a good metal, they travel far more freely than electrons attached to atoms (as in glass), allowing them to accelerate and absorb energy from the light wave's electric field. As a result, they are extremely efficient at converting energy from light waves to heat.
Q3) What about Equipartition of Energy?
A3)
The energy equipartition is a key conclusion of classical statistical mechanics: for a system in thermal equilibrium, each degree of freedom has an average energy of 12kBT. (Boltzmann's constant is kB.) Thus molecules in a gas have average kinetic energy 32kBT, 12kBT for each direction, and a simple one-dimensional harmonic oscillator has total energy kBT: 12kBT kinetic energy and 12kBT potential energy.
Comparing now the formula for the number of modes N(f)Δf in a small interval Δf
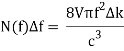
With Planck’s formula for radiation energy intensity in the same interval:
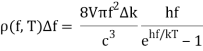
For the low frequency modes hf≪kBT we can make the approximation
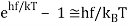
And it follows immediately that each mode has energy kBT, in line with classical predictions.
However, things go horribly wrong on a regular basis! The number of modes grows indefinitely, but the energy in these high-frequency modes decreases exponentially as the frequency rises. This was eventually termed the UV catastrophe by Ehrenfest. Rayleigh's sound strategy didn't appear to be that sound after all—something vital was lacking.
Planck never discussed equipartition, which is maybe unexpected. Of fact, as Rayleigh pointed out, equipartition was recognised to have issues, such as in the case of gas specific heat. In truth, Planck was unsure about the existence of atoms, writing subsequently that “I had been inclined to oppose atomism” in the 1890s (see notes). Even Boltzmann was unclear how successfully oscillators achieved thermal equilibrium with electromagnetic radiation—after all, it was well known that diatomic molecules oscillated with kinetic energy but did not achieve classical thermal equilibrium. (Maxwell observed that hot gases generate light at specific frequencies as early as 1877.) The oscillations must be simple harmonic because the frequencies do not change with temperature—but such an oscillator would surely be activated by collisions at low temperatures, so why wasn't energy delivered into this mode?)
Q4) Short Note on Wien’s Displacement Law.
A4)
Wien's Displacement Law is easily deduced from Planck's formula: the highest radiation per unit frequency range occurs at the frequency f for which the function f3/(ehf/kBT1) is at its maximum. Numerically, hfmax=2.82kBT is obtained.
The equation linking the frequency of maximum energy intensity in units of Joules/m3/Hz may be established theoretically (and is proven experimentally) as fmax=5.881010 T Hz/K.
The law is frequently expressed in terms of the wavelength at which the intensity, now measured in Joules/m3/m, or per unit interval of wavelength, and
2.910-3 TmK is the maximum value.
The crucial thing to remember here is that these calculations do not produce the same result, as can be easily confirmed, because fmaxmax1.7108m/sec is not the same as the speed of light! Because the two measurements, per unit interval of frequency and per unit interval of wavelength, are distinct, a claim that, for example, sunlight is most intense in the yellow must explain which one is being utilised (actually it would be wavelength, frequency would give the near infrared).
An Excel spreadsheet was used to create the graphs of black body radiation as a function of temperature. You are invited to download and experiment with this spreadsheet to see how radiation varies with temperature. It's simple to use—all you have to do is enter the temperature and see the graph change.
Q5) Explain the Applications of Photoelectric effect.
A5)
Photoelectric devices have a number of advantages, including creating a current that is precisely proportional to light intensity and having a very fast response time. The photoelectric cell, often known as a photodiode, is a simple device. This was originally a phototube, a vacuum tube with a metal cathode with a tiny work function that allowed electrons to be easily emitted. An anode held at a large positive voltage compared to the cathode would collect the current produced by the plate. Phototubes have been phased out in favour of semiconductor-based photodiodes, which can detect light, quantify its intensity, operate other devices in response to illumination, and convert light to electrical energy. These devices operate at low voltages, similar to their bandgaps, and are utilised in a variety of applications including industrial process control, pollution monitoring, light detection in fibre optic telecommunications networks, solar cells, imaging, and many more.
Semiconductors with bandgaps that correspond to the photon energy to be sensed make up photoconductive cells. Photographic exposure metres and automatic street lighting switches, for example, function in the visible spectrum and are often constructed of cadmium sulphide. Lead sulphide or mercury cadmium telluride can be used to make infrared detectors, such as night-vision sensors.
A semiconductor p-n junction is commonly used in photovoltaic devices. Solar cells are typically built of crystalline silicon and convert approximately 15% of incident light energy into electricity. Solar cells are frequently utilised in specialised contexts such as space satellites and remote telephone sites to produce very tiny amounts of power. Solar power may become economically viable for large-scale applications when cheaper materials and higher efficiency become available.
The photomultiplier tube is a very sensitive extension of the phototube, which contains a sequence of metal plates called dynodes and was first created in the 1930s. When light strikes the cathode, electrons are released. These are drawn to the first dynode, where they release more electrons, which then strike the second, and so on. The photocurrent is boosted so much after up to ten dynode stages that some photomultipliers can almost detect a single photon. In spectroscopic research, where it is frequently necessary to monitor extremely faint light sources, these devices, or solid-state counterparts of comparable sensitivity, are important. They're also employed in scintillation counters, which have a substance that creates light flashes when X-rays or gamma rays strike it, as well as a photomultiplier that counts and measures the strength of the flashes. These counters are employed for things like recognising certain isotopes for nuclear tracer analysis and detecting X-rays in computerised axial tomography (CAT) scans, which show a cross section of the body.
Q6) What is Compton Effect? Explain its Derivation.
A6)
The Compton effect is the phenomenon that occurs when x-rays or gamma rays are scattered on a substance with increasing wavelength. In the year 1922, Arthur Compton investigated this phenomenon. Compton discovered that wavelength is unaffected by incident radiation intensity during his research. It is determined by the scattering angle as well as the wavelength of the incident beam. It is expressed mathematically as follows:
What is the location?
The angle at which light is scattered
m0: an electron's rest mass
h/m0c : The electron's Compton wavelength
The peaks of the radiation spectrum are denoted by the letters s and 0.
Derivation of Compton effect equation
Considering the elastic collide between a photon and an electron, following is the derivation:
hν0 : energy of photon
Pi=hν0/c :momentum of the photon
Pi=pfcosΘ+pecosϕ(1) (conservation of momentum in x direction)
0=−pfsinΘ+pesinϕ(2) (conservation of momentum in y direction)
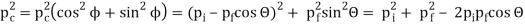
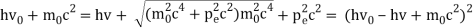
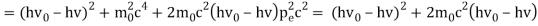
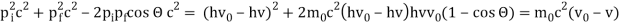

Therefore, above is the Compton effect equation andhm0c≡λc is Compton wavelength of an electron.
Q7) Difference Between Compton Effect and Photoelectric Effect.
A7)
Compton effect | Photoelectric effect |
This is the result of high-energy photons being bound to free electrons dispersing inelastically. | When electromagnetic radiation interacts with electrons, weakly bound electrons are expelled from the surface of the material, causing this effect. |
The effect was explained by Arthur Compton. | The effect was explained by Albert Einstein. |
The free electrons have a mid-energy level of energy. | The electrons have a low-energy associated with them. |
The dispersed photon has a longer wavelength than the incident photon. | The photon vanishes after interacting with the electrons, therefore the wavelength isn't visible. |
Q8) What is Wave-Particle Duality: Light?
A8)
Does light consist of particles or waves? When one focuses upon the different types of phenomena observed with light, a strong case can be built for a wave picture:


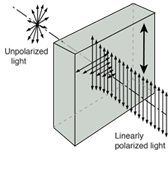
Fig. Interference Diffraction Polarization
Phenomenon | Can be explained in | Can be explained in |
Reflection |  |  |
Refraction |  |  |
Interference |  |  |
Diffraction |  |  |
Polarization |  |  |
Photoelectric effect |  |  |
Waves can explain the majority of regularly observed light phenomena. However, the photoelectric effect suggested that light has a particle nature. Then electrons were discovered to have multiple natures as well.
There is a lot of debate in the literature concerning whether light reflection and refraction can be represented in particle terms at an interface when the medium changes. Treating light as a wave phenomenon is sufficient for practical geometrical optics applications.
Q9) Define Atomic spectra and Explain Spectral Series of Hydrogen Atom.
A9)
An electron's spectrum of electromagnetic radiation released or absorbed as it moves between different energy levels within an atom.
When an electron moves from one energy level to the next, it emits or absorbs light of a given wavelength. The atomic spectra of atoms is the collection of all these unique wavelengths of the atom in a certain set of variables such as pressure, temperature, and so on. Emission spectra, absorption spectra, and continuous spectra are the three forms of atomic spectra.
Spectral Series of Hydrogen Atom
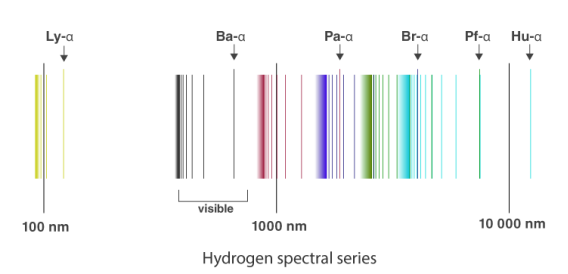
The atomic hydrogen emission spectrum is divided into a number of spectral lines with wavelengths determined by the Rydberg formula, as seen in the image above. The atomic transitions between different energy levels cause the observed spectral lines in the hydrogen emission spectrum. In astronomical spectroscopy, spectral series are crucial.
Q10) What is Hydrogen spectrum?
A10)
The hydrogen spectrum is a crucial piece of evidence for demonstrating an atom's quantized electronic structure. When an electric discharge is conducted across a gaseous hydrogen molecule, the hydrogen atoms in the molecule dissociate. The energetically excited hydrogen atoms emit electromagnetic radiation as a result of this process. The hydrogen emission spectrum is made up of discrete frequency radiation. These radiation series bear the names of the scientists who discovered them.
The spectral lines of the hydrogen atomic emission spectrum are explained by Bohr's hypothesis. The energy of an atom's electron remains unaltered while it is in the ground state. The electron jumps from the ground state orbit to a more distant excited state orbit when the atom absorbs one or more quanta of energy. The variable n is used to identify energy levels. n = 1 is the ground state, n = 2 is the first excited state, and so on. The difference in energy between the two energy levels is equal to the energy obtained by the atom. When the atom relaxes back to a lower energy state, energy equal to the difference in energy between the two orbits is released (see Figure 1).
According to the equation E = hv, the change in energy, E, causes light of a specific frequency to be emitted. Remember that the atomic emission spectrum of hydrogen has four different frequency spectral lines? The finding that electron orbits are not evenly spaced is explained in the Bohr model. The spacing between the levels gets narrower and smaller as the energy travels further away from the nucleus.
Bohr was able to calculate the energies that the hydrogen electron would have in each of its permissible energy levels using the wavelengths of the spectral lines. The energy level transitions that corresponded to the spectral lines in the atomic emission spectrum were then mathematically demonstrated ( Figure 2).
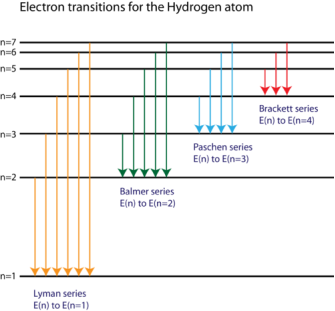
Figure. The electron energy level diagram for the hydrogen atom.
Q11) Give Explanation of the Emission Spectrum.
A11)
A theoretical explanation of the spectrum of radiation released by a glowing object was offered by Max Planck. He proposed that the walls of a glowing solid may be visualised as a set of resonators oscillating at various frequencies. These resonators absorb energy from the object's walls in the form of heat and release it in the form of electromagnetic radiation. At any given time, the energy of these resonators is proportional to the frequency with which they vibrate.
Planck had to postulate that the energy of these oscillators could only take on a restricted number of values in order to suit the observed spectrum. To put it another way, the energy spectrum for these oscillators was no longer continuous. These oscillators are theoretically "countable" since the number of possible energy levels is restricted. As a result, the energy of the oscillators in this system is quantized. To explain how light was emitted, Planck created the concept of quantization.
Planck's work was extended by Albert Einstein to include the light that had been emitted. Einstein proposed that light acted like a stream of little bundles, or packets, of energy, at a time when everyone accepted that light was a wave (and thus continuous). To put it another way, light was quantized as well. Einstein's model was predicated on two premises. To begin, he assumed that light was made up of photons, which are small, distinct energy bundles. He also assumed that a photon's energy is related to its frequency.
E = hv
In this equation, h is a constant known as Planck's constant, which is equal to 6.626 x 10-34 J-s.
Calculate the energy of a single photon of red light with a wavelength of 700.0 nm and a mole of these photons as an example.
The frequency of red light with a wavelength of 700.0 nm is 4.283 x 1014 s-1. When this frequency is substituted into the Planck-Einstein equation, the following conclusion is obtained.
E = ( 6.626 × 10-34 J-s)( 4.283 × 1014s-1) = 2.838 × 10-19 J
A single photon of red light carries an insignificant amount of energy. But a mole of these photons carries about 171,000 joules of energy, or 171 kJ/mol.
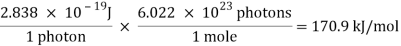
A mole of red light absorbed would thus give enough energy to raise the temperature of a litre of water by more than 40 degrees Celsius.
Because hydrogen atoms can only produce or absorb radiation at a restricted number of frequencies, they can only absorb radiation with a restricted range of energies. This indicates that the hydrogen atom contains a finite number of energy levels. These energy levels can be measured. The hydrogen atom's energy levels are quantized.
Q12) Rutherford's Scattering Experiment and Explain Its Observations.
A12)
Rutherford's model of an atom:
Ernest Rutherford was fascinated by the arrangement of electrons within an atom. For this, Rutherford devised an experiment. Fast moving alpha ()-particles were created to fall on a thin gold foil in this experiment.
- He used gold foil because he wanted the layer to be as thin as possible. The thickness of this gold foil was around 1000 atoms.
- -particles are helium ions with two charges. The fast-moving -particles have a lot of energy since they have a mass of four.
- The sub-atomic particles in gold atoms were expected to deflect -particles. He didn't anticipate to detect substantial deflections because the -particles were much heavier than the protons. The -particle scattering experiment, on the other hand, yielded completely unexpected findings.
Observations of Rutherford's scattering experiment:
As we can see in Fig.
- Most of the fast moving α-particles passed straight through the gold foil.
- Some of the α-particles were deflected by the foil by small angles.
- Surprisingly one out of every 12,000 alpha particles appeared to rebound.

Q13) Short note on Rutherford atomic model.
A13)
The atom, according to physicist Ernest Rutherford, is a miniature solar system with electrons orbiting a heavy nucleus and essentially empty space, with the nucleus occupying only a small proportion of the atom. When Rutherford suggested his concept, which featured a nucleus made entirely of protons, the neutron had not yet been identified.
To account for the scattering of alpha particles from thin gold foil reported in a series of experiments conducted by undergraduate Ernest Marsden under the direction of Rutherford and German scientist Hans Geiger in 1909, the nucleus was proposed as small and dense. Within a protective lead shield, a radioactive source generating alpha particles (positively charged particles equivalent to the helium atom nucleus and 7,000 times more heavy than electrons) was contained. After passing through a slit in a lead screen, the radiation was focussed into a narrow beam. To detect alpha particles, a thin section of gold foil was placed in front of the slit, and a screen coated with zinc sulphide to make it luminous acted as a counter. Each alpha particle created a scintillation when it hit the fluorescent screen, which was seen through a viewing microscope mounted to the rear of the screen. Rutherford and his colleagues were able to move the screen around to see if any alpha particles were being deflected by the gold foil.
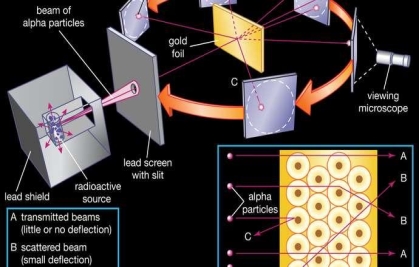
Q14) Short note on Bohr’s Model of the Hydrogen Atom.
A14)
In terms of atomic structure, Bohr's model of the hydrogen atom is the first to correctly explain the radiation spectra of atomic hydrogen. The model holds a unique place in physics history since it introduced an early quantum theory, which sparked new scientific thought and eventually led to the development of quantum mechanics. To grasp the details of Bohr's model, it's necessary to first review the nineteenth-century discoveries that led to its creation.
Using a prism to investigate white light from the sun, we may see various dark lines in the solar spectrum ((Figure)). Fraunhofer lines are named after Joseph von Fraunhofer, who properly calculated the wavelengths of solar absorption lines. Gustav Kirchhoff and Robert Bunsen found that the line emission spectra of a chemical element exactly matches its line absorption spectrum between 1854 and 1861. The distinction between the absorption and emission spectra is described in (Figure). When light passes through a gas, it produces an absorption spectrum. On the background of the continuous spectrum of white light, this spectrum appears as black lines that only exist at certain wavelengths ((Figure)). The wavelengths that are lacking indicate which wavelengths of radiation are absorbed by the gas. When a gas emits light, the emission spectrum is detected. Colorful lines on a dark backdrop represent the spectrum (see (Figure) and (Figure)). The positions of the emission lines reveal the wavelengths of radiation the gas emits. Each chemical element emits a distinct spectrum of light. The positions of each element's emission lines are identical to the positions of its absorption lines. This means that atoms of a certain element absorb only specified wavelengths of radiation, and that radiation that does not have these wavelengths is not absorbed at all. This also means that the wavelengths of the radiation emitted by each element's atoms are identical to the wavelengths of the energy they absorb.
In the solar emission spectrum in the visible range from 380 nm to 710 nm, Fraunhofer lines are observed as vertical black lines at specific spectral positions in the continuous spectrum. Thousands of similar lines are detected by highly sensitive contemporary devices.

Line spectra observation: (a) absorption lines are observed; (b) emission lines are observed. (a) White light travels through a glass flask containing a chilly gas. The wavelengths of the passing light are separated using a prism. Some wavelengths in the spectrum of the passing light are missing, resulting in black absorption lines in the continuous spectrum on the viewing screen. (b) A gas is held in a glass discharge tube with electrodes on both ends. The gas glows when there is a large potential difference between the electrodes, and the light it emits passes through the prism that separates its wavelengths. Only specified wavelengths are present in the emitted light's spectrum, which are visible on the screen as multicoloured emission lines.
Q15) Give Introduction to Atomic Spectroscopy.
A15)
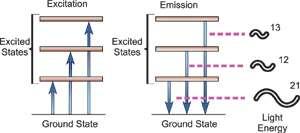
Fig. Energy Transitions
Atomic spectroscopy is the study of an element's electromagnetic or mass spectrum to determine its composition. Optical Atomic Spectroscopy is the study of an element's electromagnetic spectrum. Within an atom, electrons exist in different energy states. Electrons travelling between these levels must absorb or emit energy equal to the difference in their energies. The energy absorbed to shift an electron to a higher energetic energy level and/or the energy emitted as the electron goes to a less energetic energy level is measured in photons in optical spectroscopy. The electronic transition that has happened is closely related to the wavelength of the emitted radiant radiation. The wavelength of light emitted is a unique attribute of each individual element because each has its own electrical structure. Because a large atom's orbital structure can be complicated, several electronic transitions can occur, each of which results in the emission of a specific wavelength of light, as seen below.
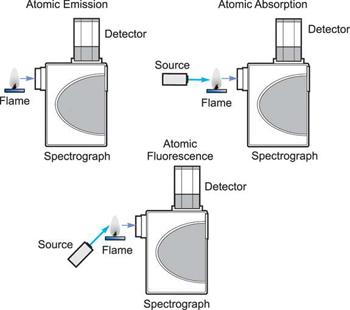
How the three techniques are implemented.
Three analytical approaches have emerged from the study of atomic spectroscopy: Atomic Absorption is a term that refers to the process of absorbing Emission of atoms. Fluorescence of atoms. In all three domains of atomic spectroscopy, the process of excitation and decay to the ground state is involved. The energy received in the excitation process or the energy emitted in the decay process is measured and analysed.
When a free, ground state atom is struck by light of just the correct wavelength, the atom may absorb the light as it transitions to an excited state, a process known as atomic absorption. On the right, you can see how this works. The amount of light at the resonant wavelength that is absorbed as it travels through a cloud of atoms is referred to as atomic absorption. The amount of light absorbed grows in a predictable manner as the number of atoms in the light path rises. A quantitative determination of the amount of analyte element present can be made by measuring the amount of light absorbed. Individual elements can be determined quantitatively in the presence of others using special light sources and careful wavelength selection. Providing enough heat energy to the sample to breakdown the chemical compounds into free atoms produces the atom cloud required for atomic absorption measurements. This is accomplished by aspirating a sample solution into a flame aligned with the light beam. Most atoms will remain in the ground state at the right flame conditions and will be able to absorb light at the analytical wavelength from a source lamp. Because of the ease and speed with which precise and accurate assessments can be produced, atomic absorption has become one of the most preferred methods for determining metals.
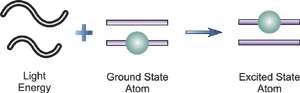
The atomic absorption process
A sample is exposed to a high-energy, thermal environment in order to develop excited state atoms capable of producing light in atomic emission. An electrical arc, a flame, or, more recently, a plasma can all be used as energy sources. Because of the discrete nature of the emitted wavelengths, the emission spectrum of an element exposed to such an energy source consists of a collection of the permissible emission wavelengths, generally referred to as emission lines. This emission spectrum can be used to qualitatively identify an element by its emission spectrum. In qualitative analysis, atomic emission utilising electrical arcs has been widely employed. Emission techniques can also be used to figure out how much of a particular element is in a sample. The intensity of light emitted at the wavelength of the element to be evaluated is measured for a "quantitative" analysis. As the number of atoms in the analyte element rises, the emission intensity at this wavelength increases. Flame photometry is a technology that uses atomic emission to do quantitative analysis.
Q16) Explain Bohr correspondence principle.
A16)
Despite the prominence of this interpretation in the physics literature, current Bohr scholars agree that Bohr did not mean his correspondence principle to indicate some form of general necessity that quantum mechanics retrieve the predictions of classical mechanics in the classical limit (see Section 6). There is less agreement, however, on which relationship between classical and quantum mechanics Bohr meant the correspondence principle to designate. In the literature, there are three main contenders, all of which are supported by Bohr's publications. The frequency interpretation, the intensity interpretation, and the selection rule interpretation are the three interpretations that can be labelled.
The correspondence principle is characterised by the frequency interpretation as a statistical asymptotic agreement between the (quantum) frequency, vn′Vn", of radiation released in a quantum leap of difference from state n′ to n′′ and the (classical) frequency () in the n′ stationary state, namely
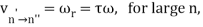
Where, n′−n′′=τ
It's worth noting that this equality between the quantum frequency and one component of the classical frequency applies only in the case of large quantum numbers—it doesn't hold for low quantum-number transitions. Furthermore, there is only statistical agreement because classically all the frequencies will be given off together, whereas quantum mechanically only a single photon with a single frequency is emitted in any given transition between stationary states; thus, one must compare the classical spectrum with a statistical ensemble of atoms.
The correspondence principle, according to the intensity interpretation, is described as the agreement, in the limit of large quantum numbers, between the probability, Pn′n", of a transition between two stationary states separated by and the square of the amplitude, C, of the classical motion:

Thus in the limit of large nn the amplitudes of the harmonic components of the electron’s classical orbit can be used to calculate the intensities of the spectral lines. While the amplitude of radiation determines its intensity in classical physics, the number of photons released at a given frequency determines the intensity of a spectral line in quantum physics. As a result, the more likely a quantum transition is, the more photons will be emitted, and the higher the intensity. It's worth noting that, like the frequency interpretation, this is merely a statistical relationship that holds only in the case of big quantum numbers.
Bohr's correspondence principle is best understood as the assertion that each permissible quantum transition between stationary states corresponds to one harmonic component of classical motion, according to the selection rule interpretation. More precisely, Bohr’s selection rule states that the transition from a stationary state n′ to another stationary state n′′ is allowed if and only if there exists a τth harmonic in the classical motion of the electron in the initial stationary state; if there is no τth harmonic in the classical motion, then transitions between stationary states whose separation is τ are not allowed quantum mechanically. Figure 1 depicts the essence of Bohr's correspondence principle.
Q17) Explain Frank hertz experiment.
A17)
The hydrogen atom's Bohr model was effective in that it accurately explained the spectrum of radiation emitted by these atoms. In essence, the model suggested the presence of discrete electronic energy levels in atoms, which could be estimated based on the assumption that the circling electrons' angular momentum was quantized. The spectrum of atomic hydrogen was explained using a combination of the concept of quantized energy levels and the idea that a quanta of radiation can only be released (with frequency determined by the Einstein relation) when an atom shifts its energy to a more tightly bound state. Other methods of obtaining more direct proof of the existence of distinct energy levels in atomic systems exist, though. The effect of hitting mercury atoms with electrons will be investigated in this experiment. Because atoms are thought to have discrete energy levels, one would anticipate energy to be transferred to the atom in distinct amounts after collisions with electrons. Inelastic scattering is one proposed process, in which a defined quantity of transmitted electron energy is absorbed by the entire atom, raising it to an excited state. The mechanics of such a collision allow the atomic system to absorb practically all of the energy of the input electron, as long as the atom does not become ionised. In 1914, Franck and Hertz attempted to validate these notions for the first time. Specifically, that atomic systems contain discrete energy levels that can be stimulated by bombardment electron collisions, and that the energy differences between the levels correspond to spectroscopic measurements. Using mercury vapour, we will perform the Franck-Hertz experiment. The wavelength of the spectral line detected in mercury discharges, which corresponds to the energy levels we will detect, is 2537. There are many additional lines in the mercury spectra, but using a Franck-Hertz setup, it is extremely difficult to excite these energy differences in the mercury atom.
Q18) What Equipment used in Frank hertz experiment.
A18)
Figure 1 shows a diagram of the equipment that will be used. It consists of a thermionic tube with a cathode, an anode, and a collector or counter electrode as the third electrode. A little blob of mercury is also present in the tube. The tube is grounded by the metal case that surrounds it. To keep a mercury vapour pressure in the tube, the mercury is heated to 180 degrees Celsius. Of course, pressure varies with temperature, and the amount of pressure is crucial to the experiment. There may be too few mercury atoms to create noticeable effects if the vapour density is too low. When the pressure is too high, the mean free path is reduced, and thermal agitation occurs.
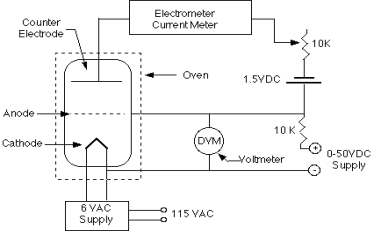
In relation to the cathode, the anode is connected to a variable voltage source (0 to +50 Volts). In relation to the anode, the counter electrode is kept at a voltage of 0.5 to 1.5 volts negative. A voltage divider and a 1.5 volt battery can be used to control the counter electrode voltage.
The cathode-anode system essentially functions as a diode. Some electrons can travel through the anode, which is a grid-like structure, and overcome the 0.5 - 1.5 Volts retarding potential to reach the counter electrode if they are energetic enough. The Keithley Electrometer, which is a very sensitive device capable of measuring the little current involved, can be used to measure the counter current.
However, we must evaluate how the presence of mercury vapour alters the system's behaviour. The mercury atoms will collide with electrons propelled from the cathode to the anode. When electrons gain enough energy to inelastically excite a mercury atom, they can lose the majority of their energy. It may therefore be unable to overcome the 0.5 - 1.5 Volts required to reach the counter electrode due to a lack of energy. As the anode voltage is increased, the counter current should drop sharply at the energy level where such collisions can occur. The counter current begins to grow again at greater voltages, but the electrons eventually accumulate enough energy to experience two or more inelastic collisions. As a result, the observed current-voltage curve should be continuously rising with a sequence of dips; the difference in energy between the ground state and first excited state in the mercury atoms will correspond to the interval of two dips.
Q19) Short note on Data Analysis in Frank hertz experiment.
A19)
For each data set, graph current vs. Voltage.
- Calculate the amount of energy transferred from an electron to a mercury atom in an inelastic collision using your graphs.
- Compare this to the projected energy from the spectral line 2537. Estimate Planck's constant using the energy given above and the 2537 spectral line (with associated uncertainty).
- To extract an electron from a metal, a specific minimum energy is required; this is referred to as the metal's "work function." The anode's work function is higher than the cathode's, resulting in a "contact-potential differential" between the anode and the cathode. It causes the entire Current vs. Voltage curve to change (why?). Calculate the difference in contact potential.
- Describe the characteristics of the detected counter current. Temperature, vapour pressure, accelerating voltage, space charge, and other physical events influence these characteristics. Make sure to bring these up in your conversation. One of the references given below may be of assistance to you.
Q20) Short note on Sommerfeld atom model.
A20)
Sommerfeld made two major changes to Bohr's theory in order to explain the observed fine structure of spectral lines.
I According to Sommerfeld, an electron's route around the nucleus is a general ellipse with the nucleus as one of its foci.
(ii) The electron's velocity in an elliptical orbit change at different points along the orbit. The mass of the travelling electron varies relativistically as a result of this.
When elliptical orbits are allowed, there are now two variables to consider.
(i) The electron's fluctuating distance from the nucleus (r).
(ii) The azimuthal angle, which describes the changing angular location of the electron with regard to the nucleus (Fig).

Two quantum numbers are introduced to cope with these two variables.
(i) In Bohr's theory, the primary quantum number n governs the energy of the electrons, and
(ii) an orbital (or azimuthal) quantum number (l) that has been introduced to characterise the angular momentum in an orbit, i.e., it determines the electron's orbital angular momentum. Its values range from zero to (n-1) in unity steps.
This orbital quantum number (l) can be used to calculate the number of potential elliptical orbits. The elliptical orbits that are possible are such that
b/a = l+1/n
Where a and b are the ellipse's semi-major and semi-minor axes, respectively.
Sommerfeld's model states that for any principal quantum number n, there are n potential sub-orbits or sub-shells with various eccentricities. One of the n subshells is circular, whereas the others (i.e., n-1) are elliptical
Because of the relativistic difference in electron mass, these hypothetical sub-orbits have slightly different energies