Unit - 3

Nuclear Physics- I

Q1) Define Atomic Nucleus.

A1)

The atomic nucleus is the nucleus, which is the most central part of the atom. Protons and neutrons are the two types of subatomic particles that make up the nucleus.

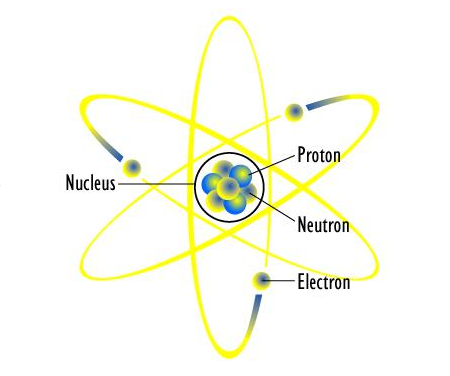
Atoms are the fundamental constituents of all substance. Atoms make up everything you can see, feel, and touch. Even things that you can't see, feel, hear, or touch are made up of atoms. Atoms are the building blocks of everything.

The Gold Foil Experiments were conducted by Ernest Rutherford and Hans Geiger and Ernest Marsden in 1909. They shot particles through exceedingly thin sheets of gold foil during the experiments. In 1911, Rutherford came to the conclusion that the atom had a dense nucleus because most of the particles shot straight through, but some of the particles were deflected due to the dense nucleus of the gold atoms. This notion would disprove the concept that the atom was more like plum pudding in structure. Until Rutherford's discoveries, the plum pudding model was the predominant model of atomic structure.

Q2) Write a Short note on Structure of the nucleus.

A2)

Because the electron and proton were the only known particles at the time, the nucleus' structure was poorly understood. It had already been proven that nuclei are typically roughly twice as heavy than protons alone can account for. Until English scientist James Chadwick discovered the neutron in 1932, a consistent hypothesis was impossible. He discovered that when alpha particles collided with beryllium nuclei, neutral particles of roughly the same mass as protons were ejected. Almost all nuclear processes may be explained in terms of neutrons and protons in a nucleus. Surprisingly, the nucleus' neutrons and protons move in orbitals to a significant extent, as if their wave functions are independent of one another. A stationary wave pattern featuring peaks and nodes, as well as angular momentum quantum numbers, describes each neutron or proton orbital. The shell nuclear model is a nucleus theory that is based on these orbitals. It was independently introduced in 1948 by Maria Goeppert Mayer of the United States and Johannes Hans Daniel Jensen of West Germany, and it grew into a full theory of the nucleus during the following decades.

Enrico Fermi, an Italian-born American physicist, and others researched the interactions of neutrons with nuclei in the mid-1930s. Neutrons, unlike protons or alpha particles, are not repelled from the nucleus by a positive charge, hence they are easily captured. When a neutron is captured, the atomic mass of the new nucleus increases by one unit. If a more stable isotope of that atomic mass is close, the new nucleus will be radioactive, converting the neutron to a proton and taking on the more stable form.

In 1938, German chemists Otto Hahn and Fritz Strassmann discovered nuclear fission as a result of experiments initiated and explained by Austrian physicist Lise Meitner. In fission, a uranium nucleus captures a neutron and gains enough energy to cause the nucleus to split into two lighter nuclei of nearly equal size due to its inherent instability. More neutrons are released during the fission process, which can be exploited to induce more fissions. Under Fermi's leadership, the first nuclear reactor, a device designed to allow controlled fission chain reactions, was built at the University of Chicago, and the first self-sustaining chain reaction occurred in this reactor in 1942. In 1945, American scientists developed the first fission weapon, also known as an atomic weapon, which employed uncontrolled fission events in uranium or plutonium. In 1952, American scientists utilised a fission explosion to start a fusion reaction, in which hydrogen isotopes thermally fused to form heavier helium nuclei. This was the world's first thermonuclear bomb, commonly known as an H-bomb, a weapon capable of releasing hundreds or thousands of times the energy of a fission bomb.

Q3) What is Probability Distribution?

A3)

Matter and photons are waves, which means they are dispersed over a large area. What is a particle's location, such as an electron's? Is it right in the middle of the tidal wave? The solution lies in how an electron's location is measured. Unlike a wave, experiments reveal that the electron will be found at a specific point. But if you set up exactly the same situation and measure it again, you will find the electron in a different location, often far outside any experimental uncertainty in your measurement. Repeated measurements will reveal a wavelike statistical distribution of sites.

Many scientists, including Schrödinger and Heisenberg, investigated the repercussions after de Broglie postulated the wave nature of matter. Because of its wave nature, it was rapidly realised that a particle's route and destination could not be anticipated precisely for each particle separately. Each particle, on the other hand, has a specific destination.

You acquire a distribution connected to the particle's wavelength and diffraction pattern after collecting enough data. The likelihood of finding the particle at a given position is known as a probability distribution, and the overall pattern is known as a probability distribution. Quantum physicists discovered equations that predicted the probability distribution in a variety of situations.

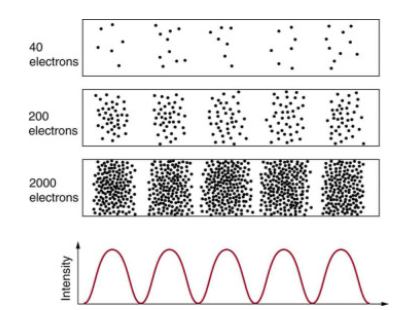
It's a little unsettling to believe that you can't foresee where a single particle will go or even follow it to its final destination. Let's see what occurs when we try to track a particle. Figure 2 shows the double-slit patterns obtained for electrons and photons. First, we observe that these patterns are similar when using d sin = m, the double-slit constructive interference equation presented in Photon Energies and the Electromagnetic Spectrum, where d is the slit separation and m is the electron or photon wavelength.

Q4) Write a Short note on Heisenberg Uncertainty.

A4)

What difference does it make knowing which slit the electron passed through make to the pattern? The response is crucial: measurement has an impact on the system being studied. Information can be lost, and it is often impossible to precisely measure two physical things at the same time. For example, scattering light or other electrons off a moving electron can be used to determine its position. Those probes have momentum of their own, and scattering from the electron causes the electron's momentum to shift in a way that causes information to be lost. Even in principle, absolute knowledge has a limit.

As a result of his work on quantum mechanics and the wave properties of all particles, Werner Heisenberg initially declared this limit to knowledge in 1929. (See Fig. 3.) Consider measuring the position and momentum of an electron at the same time (it could be any particle). Position x has an uncertainty that is roughly equal to the wavelength of the particle. x

A wave does not exist in a single location in space, as previously stated. When the position of an electron is measured repeatedly, a spread in locations is seen, signalling that position x is uncertain. We must interact with the particle in order to detect its position, such as by causing it to collide with a detector. The particle will lose momentum as a result of the collision. This change in momentum could be somewhere between zero and the particle's whole momentum.

Somewhere between zero and the particle's entire momentum, p=hp=h Because it is impossible to predict how much momentum will be transferred to a detector, momentum p is also unpredictable. In fact, the uncertainty in momentum can be as big as the momentum itself, resulting in ph in equation form.

Since x, the position uncertainty can be decreased by utilising a shorter-wavelength electron. However, because p=hp=h, reducing the wavelength increases the uncertainty in momentum. Using a longer-wavelength electron, on the other hand, reduces the uncertainty in momentum while increasing the uncertainty in location. This trade-off can be expressed mathematically by increasing the uncertainties. Xp h is left after the wavelength cancels.

As a result, if one uncertainty is lowered, the other must be increased in order for the product to be acceptable.

Heisenberg demonstrated that using advanced mathematics, the best that can be done in a simultaneous measurement of position and momentum is xph4.

The Heisenberg uncertainty principle is the name for this. With uncertainties x and p that multiply to less than h4, measuring position x and momentum p at the same time is impossible. There can't be zero uncertainty in either case. Neither uncertainty can be reduced to a small size without the other increasing in size. A narrow wavelength allows for precise location measurement, but it also increases the probe's momentum, which disrupts the momentum of the system being monitored. For example, if an electron is scattered from an atom and its wavelength is narrow enough to detect the position of electrons in the atom, the momentum of the electrons can knock them out of their orbits, causing information about their original motion to be lost. As a result, following an electron in its orbit around an atom is difficult. The electron will be found in a certain location if its position is measured, but the atom will be disrupted. Repeated measurements on similar atoms will yield intriguing probability distributions for electrons in the atom's vicinity, but not motion information. Electron clouds or orbitals are terms used to describe probability distributions.

Q5) What is Nuclear Forces?

A5)

The forces that act between two or more nucleons are known as nuclear forces (also known as nuclear interactions or strong forces). They form atomic nuclei by binding protons and neutrons ("nucleons"). The nuclear force is tens of millions of times more powerful than the chemical bonds that keep atoms in molecules together. This is why, when compared to chemical fuels like oil or coal, nuclear reactors produce around a million times more energy per kilogramme of fuel. However, the nuclear force has a limited range, only a few femtometers (1 fm =1015 m), after which it rapidly declines. That is why, despite its immense strength, we are unaware of its existence on an atomic scale or in everyday life. For seven decades, some of the world's greatest physicists have been working on a proper theory of nuclear forces, and it has been one of the most important areas of physics research in the twentieth century. The initial theory was that the force is created by the exchange of mesons, which are lighter than nucleons, and this theory spawned a new branch of modern physics known as (elementary) particle physics. The nuclear force is now thought to be a residual interaction (similar to the van der Waals force between neutral atoms) of a stronger force between quarks, which is mediated by gluon exchange and maintains quarks together inside a nucleon.

Q6) Explain Properties of the nuclear force.

A6)

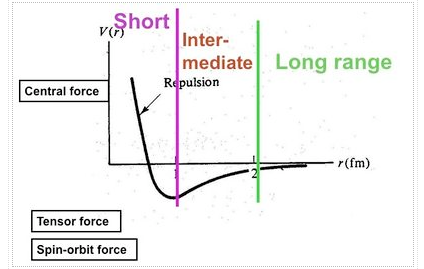
The properties of nuclei can be used to determine some properties of nuclear interactions. The volume of nuclei rises according to the quantity of nucleons, a phenomenon known as saturation. This feature implies that the nuclear (central) force has a short range (a few fm) and is extremely attracting at that range, explaining nuclear binding. The nuclear force, on the other hand, has a complex spin-dependence. The observation that the deuteron (the proton-neutron bound state, the lowest atomic nucleus) deviates somewhat from a spherical shape: it has a non-vanishing quadrupole moment was the first proof of this attribute. This proposes a force that is determined by the orientation of the nucleons' spins in relation to the vector connecting the two nucleons (a tensor force). A shell structure has been seen in heavier nuclei, which, according to M. G. Mayer and J. H. D. Jensen, can be explained by a strong force between the nucleon's spin and its orbital motion (the spin-orbit force). Scattering experiments, in which one nucleon is scattered off another nucleon with differing spin orientations, provide more direct evidence for spin dependence. The presence of the nuclear spin-orbit and tensor forces has been demonstrated in such tests. At higher energies (more than 200 MeV), scattering measurements show that the nucleon-nucleon interaction becomes repulsive at short inter-nucleon distances (smaller than 0.5 fm, the hard core).

There are three-nucleon forces (3NFs), four-nucleon forces (4NFs), and so on, in addition to the force between two nucleons (2NF). The 2NF, on the other hand, is far more powerful than the 3NF, which is far more powerful than the 4NF, and so on. The importance of 3NFs has been demonstrated in exact computations of the properties of light nuclei based on the "elementary" nuclear forces. Their contribution is tiny, yet it is critical. The necessity for 4NFs to explain nuclear properties hasn't been proven (yet).

When electromagnetic forces are neglected, nuclear forces are essentially charge-independent, meaning that the force between two protons, two neutrons, and a proton and a neutron is almost the same (in the same quantum mechanical state).

Q7) What is Phenomenological approaches?

A7)

Traditionally, nuclear force research has been divided into two categories: phenomenology and theory. To begin, we'll look at phenomenology. At very low energies, nucleon-nucleon scattering can be represented by the so-called effective range expansion, which has just two parameters in its simplest form (Bethe, 1949); for a textbook exposition, see Brown and Jackson (1976). This expansion has been recovered in modern times from an EFT that does not include the pion ('pionless EFT'); for an introduction, see Bedaque and van Kolck (2002). The spin-dependence of the nuclear force becomes significant at intermediate energies. Okuba and Marshak (1958) imposed the following symmetries to derive a general equation for the NN potential (that incorporates spin and momentum dependences):

Invariance in translation

Invariance of Galileo

Invariance of rotation

Invariance of space reflection

Invariance of time reversal

Invariance when particle 1 and 2 are interchanged

Q8) Explain Beyond the OBE approximation.

A8)

The OBE model simplifies the difficult scenario of a meson theory for the NN interaction significantly. Consequently, despite the quantitative effectiveness of the OBEPs, we should be cautious about the model's approximations. The scalar isoscalar'meson' of around 500 MeV, as well as the omission of any non-iterative diagrams, are major considerations.

The significance of meson-nucleon resonances

When two pions are 'in the air,' they can have a lot of interaction. They form a correct resonance, the meson, when in a relative P-wave (L=1). They can also interact in the form of a relative S-wave (L=0), resulting in the boson. Even though the Particle Data Group identifies a f0(500) or (500) meson with a width of 400-700 MeV, it is debatable if the is a legitimate resonance. What is certain is that two pions exhibit correlations, and if one does not believe in the existence of a two-pion resonance, one must account for these correlations. Dispersion theory and field theory are the two main methodologies for dealing with the two-pion exchange contribution to the NN interaction (which provides the intermediate range attraction).

Q9) What is QCD and the nuclear force?

A9)

The theory of strong interactions is known as quantum chromodynamics (QCD). It is part of the Standard Model of Particle Physics and deals with quarks, gluons, and their interactions. Color SU(3) is the underlying gauge group of QCD, which is a non-Abelian gauge field theory. The theory's non-Abelian character has far-reaching implications. While the interaction between coloured particles is weak at short distances or with high momentum transfer (asymptotic freedom), it is strong over long distances (1fm) or with low energies, resulting in the confinement of quarks into colourless hadrons. As a result, at high energies, QCD allows for perturbative analysis, whereas at low energies, it is highly non-perturbative. The force between nucleons is a residual colour interaction, analogous to the van der Waals force between neutral molecules, and it exists at low energies. As a result, the nuclear force is an extremely difficult issue in terms of quarks and gluons that can be tackled with brute computer power on a discretized, Euclidean space-time lattice (known as lattice QCD). The neutron-proton scattering lengths in the singlet and triplet S-waves in completely dynamical lattice QCD with a lowest pion mass of 354 MeV were found in a recent study (Beane et al., 2006). Using chiral perturbation theory, this conclusion is then extended to the physical pion mass. The 354 MeV pion mass is still too huge for meaningful extrapolations, but the feasibility has been established, and additional work is expected in the near future. The nucleon-nucleon (NN) potential was examined in a different form of lattice calculation (Hatsuda, 2012). The centre component of the potential has a repulsive core with a medium-range attraction. This is a really promising outcome, although it should be remembered that enormous pion masses are still being used in this study. In any case, advanced lattice QCD calculations are in the works and becoming better all the time. However, because these computations take a long time and are costly, they can only be used to check a few sample significant issues. A more efficient methodology is required for everyday nuclear structural physics.

Q10) Write a Short note on Power Counting.

A10)

Effective Lagrangians have an infinite number of terms, allowing for the calculation of an endless number of Feynman graphs. As a result, we require a system that allows us to handle and calculate the theory. Chiral perturbation theory is a scheme that shows us how to discern between large (important) and minor (unimportant) contributions (ChPT).

In ChPT, graphs are evaluated in terms of powers of small external momenta on a large scale: (Q/)v, where Q stands for a momentum (nucleon three-momentum or pion four-momentum) or a pion mass, and 1 GeV stands for the chiral symmetry breaking scale (hadronic scale, hard scale). Power counting is the process of determining a person's power.

Irreducible graphs are used to construct the nuclear potential. An irreducible graph, by definition, is one that cannot be divided into two by cutting just nucleon lines. A nucleon propagator is Q1, a pion propagator is Q2, each derivative in any interaction is Q, and each four-momentum integration is Q4, according to Feynman's laws of covariant perturbation theory. Naive dimensional analysis is another name for this. The power of an irreducible diagram involving A nucleons can then be calculated using some topological identities.

v = - 2 + 2A – 2C + 2L +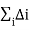

                                            (28)

With 

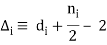
(27)

Where C is the number of separately connected pieces in the diagram and L is the number of loops; di is the number of derivatives or pion-mass insertions involved in vertex I and ni is the number of nucleon fields (nucleon legs); and the sum runs over all vertices I in the diagram under consideration. It's worth noting that i0 is true for all chiral symmetry-enabled interactions. Purely pionic interactions have at least two derivatives (di2,ni=0), pion-nucleon interactions have at least one (di1,ni=2), and nucleon-nucleon contact terms (ni=4) contain di0. This explains how chiral symmetry ensures that the expansion is low-energy.

The leading orders of connected multi-nucleon forces can be predicted using the power expression Eq. (26) Consider an A-nucleon system (mA) with an irreducibly connected m-nucleon diagram (m-nucleon force). C=Am+1 is the number of parts that are joined individually. v=2m4 is obtained by plugging this into Eq. (26) with L=0 and ii=0. Two-nucleon forces (m=2) begin at =0, three-nucleon forces (m=3) begin at =2 (but cancel in that order), and four-nucleon forces begin at =4 (they do not cancel). More on this in the following section.

For later purposes, we note that for an irreducible NN diagram (A=2, C=1), the power formula collapses to the very simple expression 

v = 2L +

(28)

In summary, the chief point of the ChPT expansion is that, at a given order ν, there exists only a finite number of graphs. This is what makes the theory calculable. The expression (Q/Λχ)ν+1 provides a rough estimate of the relative size of the contributions left out and, thus, of the accuracy at order ν. In this sense, the theory can be calculated to any desired accuracy and has predictive power.

Q11) State Two-nucleon forces: Doing the math.

A11)

We'll fill in the mathematical subtleties we left out when providing the chiral hierarchy overview in this section. The many irreducible diagrams, depicted in Figure 13 and defining the chiral NN potential order by order, are as follows:

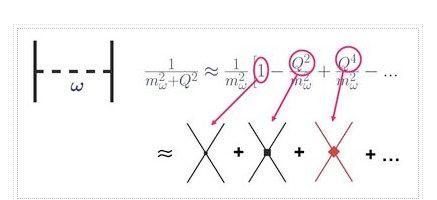
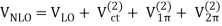
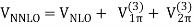
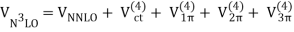
The order v of the low-momentum expansion is denoted by the superscript. The subscript "ct" denotes contact potentials, while an evident subscript denotes pion-exchange potentials.

The charge-independent 1PE potential reads 

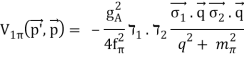
(33)

The constants' numerical values are f=92.4 MeV, gA=1.29, and m=138 MeV for the average pion mass (see Figure 5 and Eq. (23)). Because higher order corrections only affect mass and coupling constant renormalizations and there are no relativistic corrections on the shell, the on-shell 1PE has the same form as Eq. (33) at all orders.

The two zero-order contact terms at LO are 

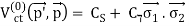
(34)

To state the mathematical expressions for 2PE contributions, we use the following scheme: 

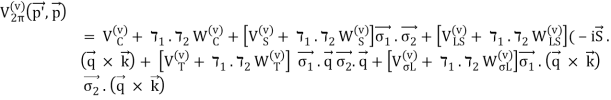(35)

Q12) Write a Short note on Three-nucleon forces.

A12)

The 2NF, of course, contributes the most to microscopic computations of nuclear structure and reactions. However, it is widely known from ab-initio investigations that 3NFs are required for precise microscopic explanation of certain few-nucleon reactions and nuclear structural difficulties. In a nutshell, 3NFs are required. As previously stated, one of the major advantages of the EFT approach to nuclear forces is that it equalises two- and many-nucleon forces (cf. Figure 13).

For a 3NF, we have A=3 and C=1 and, thus, Eq. (26) implies 

ν=2+2L+∑iΔi.(48)

We will use this equation to analyze 3NF contributions order by order.

The lowest possible power is obviously ν=2 (NLO), which is obtained for no loops (L=0) and only leading vertices (∑iΔi=0). As it turns out, this contribution vanishes.

The first non-vanishing 3NF appears at NNLO (ν=3). The power ν=3 is obtained when there are no loops (L=0) and ∑iΔi=1, i.e., Δi=1 for one vertex while Δi=0 for all other vertices. There are three topologies which fulfill this condition, known as the 2PE, 1PE, and contact graphs, Figure 17 (van Kolck, 1994), (Epelbaum et al., 2002).

The 2PE 3N-potential is derived to be

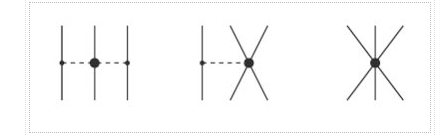
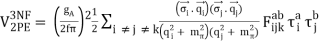
(49)

With q⃗ i≡pi→′−p⃗ i, where p⃗ i and pi→′ are the initial and final momenta of nucleon i, respectively, and 

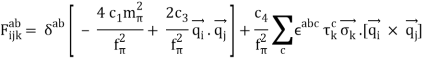
(50)

The derivations of 2PE 3NFs from conventional meson theory are very similar to this force (Fujita and Miyazawa, 1957; Coon et al., 1979).

Q13) Give Brief Introduction about Δ-isobar degrees of freedom.

A13)

The (1232) resonance or isobar (a -N P-wave resonance with both spin and isospin 3/2) has an excitation energy of M=MMN=293 MeV and is the nucleon's lowest excited state. It is an important component of models of pion-nucleon scattering in the -region and pion production from the two-nucleon system at intermediate energies, where particle production is dominated by the formation of isobars, due to its strong coupling to the -N system and low excitation energy. The virtual excitation of's, which accounts for about half of the nuclear force's intermediate-range attraction in these models at low energies—-as demonstrated by the Bonn potential—-is included in the more sophisticated conventional models for the 2-exchange contribution to the NN interaction at low energies (Machleidt et al., 1987).

Because of its tiny excitation energy, it is unclear whether the should be explicitly taken into account in an EFT or integrated out as a heavy degree of freedom. Mm, in addition to the pion mass and small external momenta, is regarded additional tiny expansion parameter if it is included. Small-scale expansion is the name given to this strategy (SSE). However, because M does not vanish in the chiral limit, this extension is phenomenological in nature.

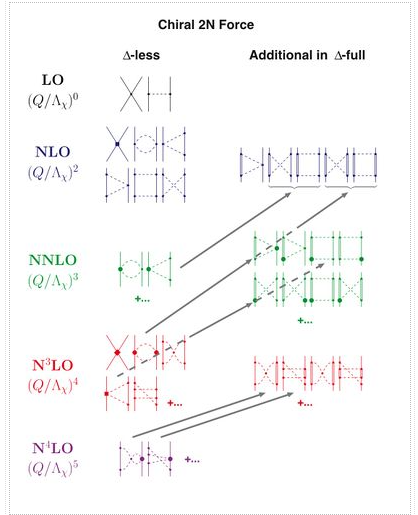
The effects of isobars are implicitly taken into consideration in the chiral EFT outlined so far (also known as the -less theory). It's worth noting that the dimension-two LECs, ci, have abnormally high values. The reason for this is that the -isobar (as well as various meson resonances) play a significant role in the ci—-a phenomenon known as resonance saturation. As a result, the explicit inclusion of the [so-called -full theory (Ordonez et al., 1996), (Kaiser et al., 1998)] detracts from the power of these LECs and shifts it to a lower order. As a result, the expansion's convergence improves, which is another reason for providing explicit -degrees of freedom. The subleading 2PE and 3PE contributions to the 2NF are bigger than the leading ones in the -less theory. The -full theory solves this problem by promoting large contributions by one order (Ordonez et al., 1996).

Q14) What is Baryon-baryon interactions?

A14)

All baryons have a significant interaction with one another. As a result, in addition to the nucleon-nucleon interactions discussed in this article, there are many additional strong baryon-baryon interactions. The forces between nucleons and hyperons (strange baryons) and hyperons and hyperons have traditionally been a focus. In addition, the contact between a baryon and an anti-baryon has piqued curiosity, with the nucleon-antinucleon contact being the most investigated. Phenomenology, meson theory, quark models, lattice QCD, and effective field theory have all been used to try to explain the baryon-(anti)baryon interactions, much as they have for the nucleon-nucleon interaction. Although it is not the goal of this article to discuss those other baryon-baryon interactions, it is worth noting that all baryon-baryon interactions are connected due to the quark sub-structure of hadrons. As a result, the nucleon-nucleon interaction covered in this paper should be viewed in the context of all baryonic interactions. Achieving a description of all baryon-baryon interactions that is consistent with all relevant underlying symmetries is a difficult task in today's study. We want to recommend interested readers to the literature for more information on this issue. Rijken et al. (2013) review hyperon-nucleon interactions in the meson image, while Haidenbauer et al. (2013) review chiral EFT. See Klempt et al. (2005) for a nucleon-antinucleon approach, and Kang et al. (2013) for a chiral EFT technique.

Q15) Describe Magic Numbers.

A15)

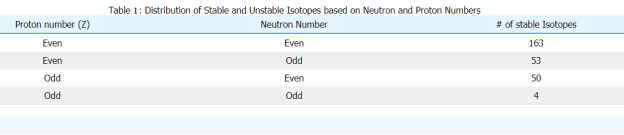
The Octet Rule was developed as a result of the discovery that atoms containing eight valence electrons were particularly stable (and common). Nuclei have a similar scenario in terms of the number of neutrons and proton quantities that produce stable (non-radioactive) isotopes. These "magic numbers" are natural occurrences in especially stable isotopes. Numbers of protons and neutrons are listed in Table 1; isotopes with these numbers in either the proton or neutron are stable. In some situations, isotopes can have magic numbers for both protons and neutrons, which are referred to as double magic numbers. Because of the repulsion of the interactions between the protons, double numbers only appear for heavier isotopes. The magic numbers are as follows:

There's also the idea that isotopes with a mix of even-even, even-odd, odd-even, and odd-odd isotopes are all stable. Even-even nuclides exist in greater numbers than odd-odd nuclides. Many isotopes with no magic number of nucleons are stable, just as there are exceptions to the octet rule.

Q16) Explain Liquid Drop Model.

A16)

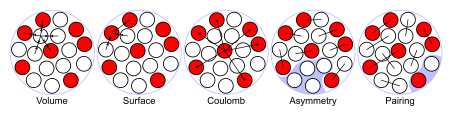
In the liquid drop model of the atomic nucleus, the terms of the semi-empirical mass formula are illustrated.

George Gamow proposed the liquid drop model, which was further developed by Niels Bohr and John Archibald Wheeler. It treats the nucleus as an incompressible fluid drop with a very high density that is held together by the nuclear force (a residual effect of the strong force), with a structure that resembles that of a spherical liquid drop. The liquid drop model, albeit primitive, accounts for most nuclei's spherical shape and offers a rough forecast of binding energy.

The mass formula is solely specified in terms of the number of protons and neutrons it contains. Five terms are defined in the original Weizsäcker formula:

●       When an assembly of nucleons of the same size is packed together into the smallest volume, each inside nucleon comes into contact with a particular number of other nucleons. As a result, the amount of nuclear energy produced is proportional to the volume.

●       The assumption that each nucleon interacts with the same number of other nucleons is corrected by surface energy. Because this term is negative and proportionate to surface area, it is nearly similar to liquid surface tension.

●       The potential energy of each pair of protons is known as Coulomb energy. The binding energy is lowered because this is a repulsive force.

●       The Pauli exclusion principle is explained by asymmetry energy (also known as Pauli Energy). Uneven quantities of neutrons and protons mean that one type of particle will fill higher energy levels while the other will leave lower energy levels empty.

●       The likelihood for proton and neutron pairs to form is explained by pairing energy. Due to spin coupling, an even number of particles is more stable than an odd number.

Q17) Explain Semi-empirical mass formula.

A17)

B/A, or binding energy per nucleon, is a common representation of binding energy. Because B/A is largely constant, the binding energy is simply proportional to A in general.

However, there are reversals in this pattern. The semi-empirical mass formula captures B/reliance A's on A (and Z). This formula is based on first-principles considerations (a nuclear force model) as well as experimental evidence to determine the specific parameters that define it. All nucleons are uniformly distributed inside a nucleus in this model, known as the liquid-drop model, and are linked together by the nuclear force, whereas the Coulomb interaction causes protons to repel one another. Part of the semi-empirical mass formula is explained by nuclear force (short range) and Coulomb interaction characteristics. Other (smaller) corrections, on the other hand, have been proposed to account for changes in the binding energy that arise due to its quantum-mechanical character (and that give rise to the nuclear shell model).

The semi-empirical mass formula (SEMF) is

M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2

Where the binding energy B(Z, A) is given by the following formula:

Q18) Write a Short note on Shell Model.

A18)

The Shell Model, for example, accounts for a number of aspects of nuclear energy levels. According to this paradigm, the average attractive force of all the other nucleons governs the mobility of each nucleon. The orbits that arise form "shells," much like the orbits of electrons in atoms. As more nucleons are introduced to the nucleus, they fall into the lowest-energy shells allowed by the Pauli Principle, which stipulates that each nucleon must have its own set of quantum numbers to describe its motion.

.

A nucleus of remarkable stability arises when a shell is full (that is, when the nucleons have used up all of the feasible sets of quantum number assignments). This is comparable to the idea found in an atom, where a filled set of electron quantum numbers produces an atom with extraordinary stability–an inert gas. The number of protons or neutrons in a nucleus is dubbed a "magic number" when all of them are in filled shells. 2, 8, 20, 28, 50, 82, and 126 are some of the magical numbers. The magic number of protons in 116Sn is 50, and the magic number of neutrons in 54Fe is 54. (28). Some nuclei, such as 40Ca and 208Pb, have magical numbers of protons and neutrons; these nuclei are referred to as "doubly magical" because of their unusual stability. On the nuclide chart, magic numbers are indicated.

The total angular momentum, J, of filled shells is zero. The J of the new ground state is determined by the next additional nucleon (a valence nucleon). When nucleons (individually or in pairs) are aroused out of the ground state, their angular momentum, as well as their parity and isospin projection quantum numbers, are altered. The shell model explains how much energy it takes to transfer nucleons from one orbit to the next, as well as how quantum numbers fluctuate. The energy diagram of the two filled shells of the 12C ground state is shown in the diagram above. When a nucleon or a pair of nucleons are promoted to an empty shell, the nucleus enters one of the excited states.

Q19) Difference Between Shell Structure of Nuclei and Shell Structure of Atom.

A19)

Q20) What is History and Origin of the term?

A20)

Maria Goeppert Mayer, a German scientist, became interested in the features of nuclear fission products, such as decay energies and half-lives, while working on the Manhattan Project. She published a body of experimental evidence supporting closed nuclear shells in nuclei with 50 or 82 protons or 50, 82, and 126 neutrons in 1948. (It was already known that nuclei with 20 protons or neutrons were stable; calculations by Hungarian-American physicist Eugene Wigner, one of her Manhattan Project colleagues, demonstrated this.) Two years later, in 1950, she published a second paper in which she blamed spin-orbit coupling for the shell closures at the magic numbers.

According to Maria Goeppert Mayer's student Steven Moszkowski, the word "Wigner coined the phrase "magic number": "Wigner, too, believed in the liquid drop model, but he recognised the very strong evidence for the closed shells from Maria Mayer's work." It appeared to him to be a little like magic, and hence the term 'Magic Numbers' was coined."

These magic numbers formed the foundation of Mayer's nuclear shell model, which he developed with Hans Jensen over the next few years and resulted in their joint Nobel Prize in Physics in 1963.

Unit - 3

Nuclear Physics- I

Q1) Define Atomic Nucleus.

A1)

The atomic nucleus is the nucleus, which is the most central part of the atom. Protons and neutrons are the two types of subatomic particles that make up the nucleus.

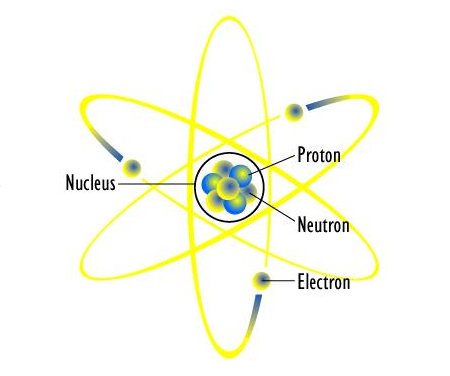
Atoms are the fundamental constituents of all substance. Atoms make up everything you can see, feel, and touch. Even things that you can't see, feel, hear, or touch are made up of atoms. Atoms are the building blocks of everything.

The Gold Foil Experiments were conducted by Ernest Rutherford and Hans Geiger and Ernest Marsden in 1909. They shot particles through exceedingly thin sheets of gold foil during the experiments. In 1911, Rutherford came to the conclusion that the atom had a dense nucleus because most of the particles shot straight through, but some of the particles were deflected due to the dense nucleus of the gold atoms. This notion would disprove the concept that the atom was more like plum pudding in structure. Until Rutherford's discoveries, the plum pudding model was the predominant model of atomic structure.

Q2) Write a Short note on Structure of the nucleus.

A2)

Because the electron and proton were the only known particles at the time, the nucleus' structure was poorly understood. It had already been proven that nuclei are typically roughly twice as heavy than protons alone can account for. Until English scientist James Chadwick discovered the neutron in 1932, a consistent hypothesis was impossible. He discovered that when alpha particles collided with beryllium nuclei, neutral particles of roughly the same mass as protons were ejected. Almost all nuclear processes may be explained in terms of neutrons and protons in a nucleus. Surprisingly, the nucleus' neutrons and protons move in orbitals to a significant extent, as if their wave functions are independent of one another. A stationary wave pattern featuring peaks and nodes, as well as angular momentum quantum numbers, describes each neutron or proton orbital. The shell nuclear model is a nucleus theory that is based on these orbitals. It was independently introduced in 1948 by Maria Goeppert Mayer of the United States and Johannes Hans Daniel Jensen of West Germany, and it grew into a full theory of the nucleus during the following decades.

Enrico Fermi, an Italian-born American physicist, and others researched the interactions of neutrons with nuclei in the mid-1930s. Neutrons, unlike protons or alpha particles, are not repelled from the nucleus by a positive charge, hence they are easily captured. When a neutron is captured, the atomic mass of the new nucleus increases by one unit. If a more stable isotope of that atomic mass is close, the new nucleus will be radioactive, converting the neutron to a proton and taking on the more stable form.

In 1938, German chemists Otto Hahn and Fritz Strassmann discovered nuclear fission as a result of experiments initiated and explained by Austrian physicist Lise Meitner. In fission, a uranium nucleus captures a neutron and gains enough energy to cause the nucleus to split into two lighter nuclei of nearly equal size due to its inherent instability. More neutrons are released during the fission process, which can be exploited to induce more fissions. Under Fermi's leadership, the first nuclear reactor, a device designed to allow controlled fission chain reactions, was built at the University of Chicago, and the first self-sustaining chain reaction occurred in this reactor in 1942. In 1945, American scientists developed the first fission weapon, also known as an atomic weapon, which employed uncontrolled fission events in uranium or plutonium. In 1952, American scientists utilised a fission explosion to start a fusion reaction, in which hydrogen isotopes thermally fused to form heavier helium nuclei. This was the world's first thermonuclear bomb, commonly known as an H-bomb, a weapon capable of releasing hundreds or thousands of times the energy of a fission bomb.

Q3) What is Probability Distribution?

A3)

Matter and photons are waves, which means they are dispersed over a large area. What is a particle's location, such as an electron's? Is it right in the middle of the tidal wave? The solution lies in how an electron's location is measured. Unlike a wave, experiments reveal that the electron will be found at a specific point. But if you set up exactly the same situation and measure it again, you will find the electron in a different location, often far outside any experimental uncertainty in your measurement. Repeated measurements will reveal a wavelike statistical distribution of sites.

Many scientists, including Schrödinger and Heisenberg, investigated the repercussions after de Broglie postulated the wave nature of matter. Because of its wave nature, it was rapidly realised that a particle's route and destination could not be anticipated precisely for each particle separately. Each particle, on the other hand, has a specific destination.

You acquire a distribution connected to the particle's wavelength and diffraction pattern after collecting enough data. The likelihood of finding the particle at a given position is known as a probability distribution, and the overall pattern is known as a probability distribution. Quantum physicists discovered equations that predicted the probability distribution in a variety of situations.

It's a little unsettling to believe that you can't foresee where a single particle will go or even follow it to its final destination. Let's see what occurs when we try to track a particle. Figure 2 shows the double-slit patterns obtained for electrons and photons. First, we observe that these patterns are similar when using d sin = m, the double-slit constructive interference equation presented in Photon Energies and the Electromagnetic Spectrum, where d is the slit separation and m is the electron or photon wavelength.

Q4) Write a Short note on Heisenberg Uncertainty.

A4)

What difference does it make knowing which slit the electron passed through make to the pattern? The response is crucial: measurement has an impact on the system being studied. Information can be lost, and it is often impossible to precisely measure two physical things at the same time. For example, scattering light or other electrons off a moving electron can be used to determine its position. Those probes have momentum of their own, and scattering from the electron causes the electron's momentum to shift in a way that causes information to be lost. Even in principle, absolute knowledge has a limit.

As a result of his work on quantum mechanics and the wave properties of all particles, Werner Heisenberg initially declared this limit to knowledge in 1929. (See Fig. 3.) Consider measuring the position and momentum of an electron at the same time (it could be any particle). Position x has an uncertainty that is roughly equal to the wavelength of the particle. x

A wave does not exist in a single location in space, as previously stated. When the position of an electron is measured repeatedly, a spread in locations is seen, signalling that position x is uncertain. We must interact with the particle in order to detect its position, such as by causing it to collide with a detector. The particle will lose momentum as a result of the collision. This change in momentum could be somewhere between zero and the particle's whole momentum.

Somewhere between zero and the particle's entire momentum, p=hp=h Because it is impossible to predict how much momentum will be transferred to a detector, momentum p is also unpredictable. In fact, the uncertainty in momentum can be as big as the momentum itself, resulting in ph in equation form.

Since x, the position uncertainty can be decreased by utilising a shorter-wavelength electron. However, because p=hp=h, reducing the wavelength increases the uncertainty in momentum. Using a longer-wavelength electron, on the other hand, reduces the uncertainty in momentum while increasing the uncertainty in location. This trade-off can be expressed mathematically by increasing the uncertainties. Xp h is left after the wavelength cancels.

As a result, if one uncertainty is lowered, the other must be increased in order for the product to be acceptable.

Heisenberg demonstrated that using advanced mathematics, the best that can be done in a simultaneous measurement of position and momentum is xph4.

The Heisenberg uncertainty principle is the name for this. With uncertainties x and p that multiply to less than h4, measuring position x and momentum p at the same time is impossible. There can't be zero uncertainty in either case. Neither uncertainty can be reduced to a small size without the other increasing in size. A narrow wavelength allows for precise location measurement, but it also increases the probe's momentum, which disrupts the momentum of the system being monitored. For example, if an electron is scattered from an atom and its wavelength is narrow enough to detect the position of electrons in the atom, the momentum of the electrons can knock them out of their orbits, causing information about their original motion to be lost. As a result, following an electron in its orbit around an atom is difficult. The electron will be found in a certain location if its position is measured, but the atom will be disrupted. Repeated measurements on similar atoms will yield intriguing probability distributions for electrons in the atom's vicinity, but not motion information. Electron clouds or orbitals are terms used to describe probability distributions.

Q5) What is Nuclear Forces?

A5)

The forces that act between two or more nucleons are known as nuclear forces (also known as nuclear interactions or strong forces). They form atomic nuclei by binding protons and neutrons ("nucleons"). The nuclear force is tens of millions of times more powerful than the chemical bonds that keep atoms in molecules together. This is why, when compared to chemical fuels like oil or coal, nuclear reactors produce around a million times more energy per kilogramme of fuel. However, the nuclear force has a limited range, only a few femtometers (1 fm =1015 m), after which it rapidly declines. That is why, despite its immense strength, we are unaware of its existence on an atomic scale or in everyday life. For seven decades, some of the world's greatest physicists have been working on a proper theory of nuclear forces, and it has been one of the most important areas of physics research in the twentieth century. The initial theory was that the force is created by the exchange of mesons, which are lighter than nucleons, and this theory spawned a new branch of modern physics known as (elementary) particle physics. The nuclear force is now thought to be a residual interaction (similar to the van der Waals force between neutral atoms) of a stronger force between quarks, which is mediated by gluon exchange and maintains quarks together inside a nucleon.

Q6) Explain Properties of the nuclear force.

A6)

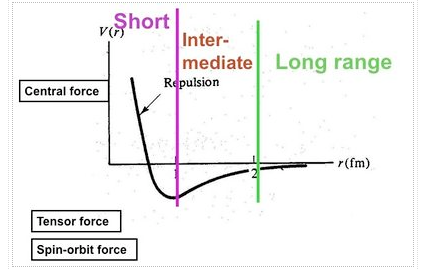
The properties of nuclei can be used to determine some properties of nuclear interactions. The volume of nuclei rises according to the quantity of nucleons, a phenomenon known as saturation. This feature implies that the nuclear (central) force has a short range (a few fm) and is extremely attracting at that range, explaining nuclear binding. The nuclear force, on the other hand, has a complex spin-dependence. The observation that the deuteron (the proton-neutron bound state, the lowest atomic nucleus) deviates somewhat from a spherical shape: it has a non-vanishing quadrupole moment was the first proof of this attribute. This proposes a force that is determined by the orientation of the nucleons' spins in relation to the vector connecting the two nucleons (a tensor force). A shell structure has been seen in heavier nuclei, which, according to M. G. Mayer and J. H. D. Jensen, can be explained by a strong force between the nucleon's spin and its orbital motion (the spin-orbit force). Scattering experiments, in which one nucleon is scattered off another nucleon with differing spin orientations, provide more direct evidence for spin dependence. The presence of the nuclear spin-orbit and tensor forces has been demonstrated in such tests. At higher energies (more than 200 MeV), scattering measurements show that the nucleon-nucleon interaction becomes repulsive at short inter-nucleon distances (smaller than 0.5 fm, the hard core).

There are three-nucleon forces (3NFs), four-nucleon forces (4NFs), and so on, in addition to the force between two nucleons (2NF). The 2NF, on the other hand, is far more powerful than the 3NF, which is far more powerful than the 4NF, and so on. The importance of 3NFs has been demonstrated in exact computations of the properties of light nuclei based on the "elementary" nuclear forces. Their contribution is tiny, yet it is critical. The necessity for 4NFs to explain nuclear properties hasn't been proven (yet).

When electromagnetic forces are neglected, nuclear forces are essentially charge-independent, meaning that the force between two protons, two neutrons, and a proton and a neutron is almost the same (in the same quantum mechanical state).

Q7) What is Phenomenological approaches?

A7)

Traditionally, nuclear force research has been divided into two categories: phenomenology and theory. To begin, we'll look at phenomenology. At very low energies, nucleon-nucleon scattering can be represented by the so-called effective range expansion, which has just two parameters in its simplest form (Bethe, 1949); for a textbook exposition, see Brown and Jackson (1976). This expansion has been recovered in modern times from an EFT that does not include the pion ('pionless EFT'); for an introduction, see Bedaque and van Kolck (2002). The spin-dependence of the nuclear force becomes significant at intermediate energies. Okuba and Marshak (1958) imposed the following symmetries to derive a general equation for the NN potential (that incorporates spin and momentum dependences):

Invariance in translation

Invariance of Galileo

Invariance of rotation

Invariance of space reflection

Invariance of time reversal

Invariance when particle 1 and 2 are interchanged

Q8) Explain Beyond the OBE approximation.

A8)

The OBE model simplifies the difficult scenario of a meson theory for the NN interaction significantly. Consequently, despite the quantitative effectiveness of the OBEPs, we should be cautious about the model's approximations. The scalar isoscalar'meson' of around 500 MeV, as well as the omission of any non-iterative diagrams, are major considerations.

The significance of meson-nucleon resonances

When two pions are 'in the air,' they can have a lot of interaction. They form a correct resonance, the meson, when in a relative P-wave (L=1). They can also interact in the form of a relative S-wave (L=0), resulting in the boson. Even though the Particle Data Group identifies a f0(500) or (500) meson with a width of 400-700 MeV, it is debatable if the is a legitimate resonance. What is certain is that two pions exhibit correlations, and if one does not believe in the existence of a two-pion resonance, one must account for these correlations. Dispersion theory and field theory are the two main methodologies for dealing with the two-pion exchange contribution to the NN interaction (which provides the intermediate range attraction).

Q9) What is QCD and the nuclear force?

A9)

The theory of strong interactions is known as quantum chromodynamics (QCD). It is part of the Standard Model of Particle Physics and deals with quarks, gluons, and their interactions. Color SU(3) is the underlying gauge group of QCD, which is a non-Abelian gauge field theory. The theory's non-Abelian character has far-reaching implications. While the interaction between coloured particles is weak at short distances or with high momentum transfer (asymptotic freedom), it is strong over long distances (1fm) or with low energies, resulting in the confinement of quarks into colourless hadrons. As a result, at high energies, QCD allows for perturbative analysis, whereas at low energies, it is highly non-perturbative. The force between nucleons is a residual colour interaction, analogous to the van der Waals force between neutral molecules, and it exists at low energies. As a result, the nuclear force is an extremely difficult issue in terms of quarks and gluons that can be tackled with brute computer power on a discretized, Euclidean space-time lattice (known as lattice QCD). The neutron-proton scattering lengths in the singlet and triplet S-waves in completely dynamical lattice QCD with a lowest pion mass of 354 MeV were found in a recent study (Beane et al., 2006). Using chiral perturbation theory, this conclusion is then extended to the physical pion mass. The 354 MeV pion mass is still too huge for meaningful extrapolations, but the feasibility has been established, and additional work is expected in the near future. The nucleon-nucleon (NN) potential was examined in a different form of lattice calculation (Hatsuda, 2012). The centre component of the potential has a repulsive core with a medium-range attraction. This is a really promising outcome, although it should be remembered that enormous pion masses are still being used in this study. In any case, advanced lattice QCD calculations are in the works and becoming better all the time. However, because these computations take a long time and are costly, they can only be used to check a few sample significant issues. A more efficient methodology is required for everyday nuclear structural physics.

Q10) Write a Short note on Power Counting.

A10)

Effective Lagrangians have an infinite number of terms, allowing for the calculation of an endless number of Feynman graphs. As a result, we require a system that allows us to handle and calculate the theory. Chiral perturbation theory is a scheme that shows us how to discern between large (important) and minor (unimportant) contributions (ChPT).

In ChPT, graphs are evaluated in terms of powers of small external momenta on a large scale: (Q/)v, where Q stands for a momentum (nucleon three-momentum or pion four-momentum) or a pion mass, and 1 GeV stands for the chiral symmetry breaking scale (hadronic scale, hard scale). Power counting is the process of determining a person's power.

Irreducible graphs are used to construct the nuclear potential. An irreducible graph, by definition, is one that cannot be divided into two by cutting just nucleon lines. A nucleon propagator is Q1, a pion propagator is Q2, each derivative in any interaction is Q, and each four-momentum integration is Q4, according to Feynman's laws of covariant perturbation theory. Naive dimensional analysis is another name for this. The power of an irreducible diagram involving A nucleons can then be calculated using some topological identities.

v = - 2 + 2A – 2C + 2L +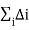

                                            (28)

With 

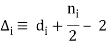
(27)

Where C is the number of separately connected pieces in the diagram and L is the number of loops; di is the number of derivatives or pion-mass insertions involved in vertex I and ni is the number of nucleon fields (nucleon legs); and the sum runs over all vertices I in the diagram under consideration. It's worth noting that i0 is true for all chiral symmetry-enabled interactions. Purely pionic interactions have at least two derivatives (di2,ni=0), pion-nucleon interactions have at least one (di1,ni=2), and nucleon-nucleon contact terms (ni=4) contain di0. This explains how chiral symmetry ensures that the expansion is low-energy.

The leading orders of connected multi-nucleon forces can be predicted using the power expression Eq. (26) Consider an A-nucleon system (mA) with an irreducibly connected m-nucleon diagram (m-nucleon force). C=Am+1 is the number of parts that are joined individually. v=2m4 is obtained by plugging this into Eq. (26) with L=0 and ii=0. Two-nucleon forces (m=2) begin at =0, three-nucleon forces (m=3) begin at =2 (but cancel in that order), and four-nucleon forces begin at =4 (they do not cancel). More on this in the following section.

For later purposes, we note that for an irreducible NN diagram (A=2, C=1), the power formula collapses to the very simple expression 

v = 2L +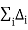

(28)

In summary, the chief point of the ChPT expansion is that, at a given order ν, there exists only a finite number of graphs. This is what makes the theory calculable. The expression (Q/Λχ)ν+1 provides a rough estimate of the relative size of the contributions left out and, thus, of the accuracy at order ν. In this sense, the theory can be calculated to any desired accuracy and has predictive power.

Q11) State Two-nucleon forces: Doing the math.

A11)

We'll fill in the mathematical subtleties we left out when providing the chiral hierarchy overview in this section. The many irreducible diagrams, depicted in Figure 13 and defining the chiral NN potential order by order, are as follows:

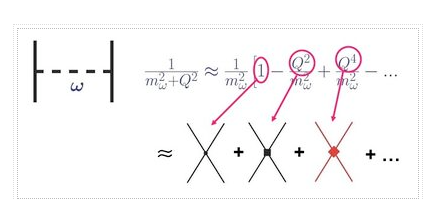
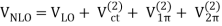
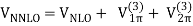
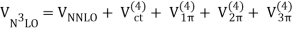
The order v of the low-momentum expansion is denoted by the superscript. The subscript "ct" denotes contact potentials, while an evident subscript denotes pion-exchange potentials.

The charge-independent 1PE potential reads 

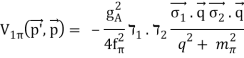
(33)

The constants' numerical values are f=92.4 MeV, gA=1.29, and m=138 MeV for the average pion mass (see Figure 5 and Eq. (23)). Because higher order corrections only affect mass and coupling constant renormalizations and there are no relativistic corrections on the shell, the on-shell 1PE has the same form as Eq. (33) at all orders.

The two zero-order contact terms at LO are 

(34)

To state the mathematical expressions for 2PE contributions, we use the following scheme: 

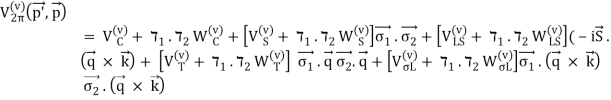(35)

Q12) Write a Short note on Three-nucleon forces.

A12)

The 2NF, of course, contributes the most to microscopic computations of nuclear structure and reactions. However, it is widely known from ab-initio investigations that 3NFs are required for precise microscopic explanation of certain few-nucleon reactions and nuclear structural difficulties. In a nutshell, 3NFs are required. As previously stated, one of the major advantages of the EFT approach to nuclear forces is that it equalises two- and many-nucleon forces (cf. Figure 13).

For a 3NF, we have A=3 and C=1 and, thus, Eq. (26) implies 

ν=2+2L+∑iΔi.(48)

We will use this equation to analyze 3NF contributions order by order.

The lowest possible power is obviously ν=2 (NLO), which is obtained for no loops (L=0) and only leading vertices (∑iΔi=0). As it turns out, this contribution vanishes.

The first non-vanishing 3NF appears at NNLO (ν=3). The power ν=3 is obtained when there are no loops (L=0) and ∑iΔi=1, i.e., Δi=1 for one vertex while Δi=0 for all other vertices. There are three topologies which fulfill this condition, known as the 2PE, 1PE, and contact graphs, Figure 17 (van Kolck, 1994), (Epelbaum et al., 2002).

The 2PE 3N-potential is derived to be

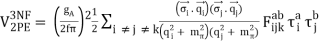
(49)

With q⃗ i≡pi→′−p⃗ i, where p⃗ i and pi→′ are the initial and final momenta of nucleon i, respectively, and 

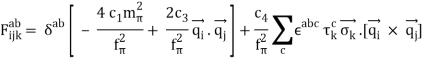
(50)

The derivations of 2PE 3NFs from conventional meson theory are very similar to this force (Fujita and Miyazawa, 1957; Coon et al., 1979).

Q13) Give Brief Introduction about Δ-isobar degrees of freedom.

A13)

The (1232) resonance or isobar (a -N P-wave resonance with both spin and isospin 3/2) has an excitation energy of M=MMN=293 MeV and is the nucleon's lowest excited state. It is an important component of models of pion-nucleon scattering in the -region and pion production from the two-nucleon system at intermediate energies, where particle production is dominated by the formation of isobars, due to its strong coupling to the -N system and low excitation energy. The virtual excitation of's, which accounts for about half of the nuclear force's intermediate-range attraction in these models at low energies—-as demonstrated by the Bonn potential—-is included in the more sophisticated conventional models for the 2-exchange contribution to the NN interaction at low energies (Machleidt et al., 1987).

Because of its tiny excitation energy, it is unclear whether the should be explicitly taken into account in an EFT or integrated out as a heavy degree of freedom. Mm, in addition to the pion mass and small external momenta, is regarded additional tiny expansion parameter if it is included. Small-scale expansion is the name given to this strategy (SSE). However, because M does not vanish in the chiral limit, this extension is phenomenological in nature.

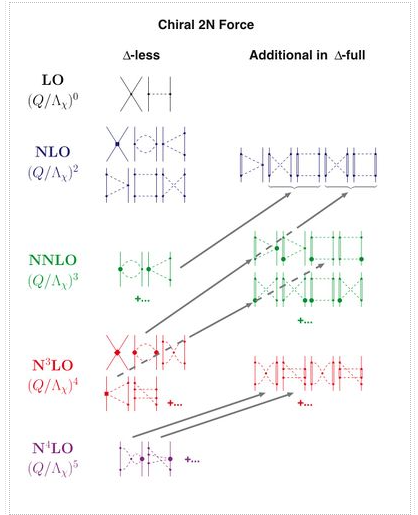
The effects of isobars are implicitly taken into consideration in the chiral EFT outlined so far (also known as the -less theory). It's worth noting that the dimension-two LECs, ci, have abnormally high values. The reason for this is that the -isobar (as well as various meson resonances) play a significant role in the ci—-a phenomenon known as resonance saturation. As a result, the explicit inclusion of the [so-called -full theory (Ordonez et al., 1996), (Kaiser et al., 1998)] detracts from the power of these LECs and shifts it to a lower order. As a result, the expansion's convergence improves, which is another reason for providing explicit -degrees of freedom. The subleading 2PE and 3PE contributions to the 2NF are bigger than the leading ones in the -less theory. The -full theory solves this problem by promoting large contributions by one order (Ordonez et al., 1996).

Q14) What is Baryon-baryon interactions?

A14)

All baryons have a significant interaction with one another. As a result, in addition to the nucleon-nucleon interactions discussed in this article, there are many additional strong baryon-baryon interactions. The forces between nucleons and hyperons (strange baryons) and hyperons and hyperons have traditionally been a focus. In addition, the contact between a baryon and an anti-baryon has piqued curiosity, with the nucleon-antinucleon contact being the most investigated. Phenomenology, meson theory, quark models, lattice QCD, and effective field theory have all been used to try to explain the baryon-(anti)baryon interactions, much as they have for the nucleon-nucleon interaction. Although it is not the goal of this article to discuss those other baryon-baryon interactions, it is worth noting that all baryon-baryon interactions are connected due to the quark sub-structure of hadrons. As a result, the nucleon-nucleon interaction covered in this paper should be viewed in the context of all baryonic interactions. Achieving a description of all baryon-baryon interactions that is consistent with all relevant underlying symmetries is a difficult task in today's study. We want to recommend interested readers to the literature for more information on this issue. Rijken et al. (2013) review hyperon-nucleon interactions in the meson image, while Haidenbauer et al. (2013) review chiral EFT. See Klempt et al. (2005) for a nucleon-antinucleon approach, and Kang et al. (2013) for a chiral EFT technique.

Q15) Describe Magic Numbers.

A15)

The Octet Rule was developed as a result of the discovery that atoms containing eight valence electrons were particularly stable (and common). Nuclei have a similar scenario in terms of the number of neutrons and proton quantities that produce stable (non-radioactive) isotopes. These "magic numbers" are natural occurrences in especially stable isotopes. Numbers of protons and neutrons are listed in Table 1; isotopes with these numbers in either the proton or neutron are stable. In some situations, isotopes can have magic numbers for both protons and neutrons, which are referred to as double magic numbers. Because of the repulsion of the interactions between the protons, double numbers only appear for heavier isotopes. The magic numbers are as follows:

There's also the idea that isotopes with a mix of even-even, even-odd, odd-even, and odd-odd isotopes are all stable. Even-even nuclides exist in greater numbers than odd-odd nuclides. Many isotopes with no magic number of nucleons are stable, just as there are exceptions to the octet rule.

Q16) Explain Liquid Drop Model.

A16)

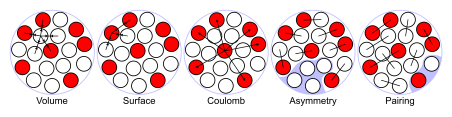
In the liquid drop model of the atomic nucleus, the terms of the semi-empirical mass formula are illustrated.

George Gamow proposed the liquid drop model, which was further developed by Niels Bohr and John Archibald Wheeler. It treats the nucleus as an incompressible fluid drop with a very high density that is held together by the nuclear force (a residual effect of the strong force), with a structure that resembles that of a spherical liquid drop. The liquid drop model, albeit primitive, accounts for most nuclei's spherical shape and offers a rough forecast of binding energy.

The mass formula is solely specified in terms of the number of protons and neutrons it contains. Five terms are defined in the original Weizsäcker formula:

●       When an assembly of nucleons of the same size is packed together into the smallest volume, each inside nucleon comes into contact with a particular number of other nucleons. As a result, the amount of nuclear energy produced is proportional to the volume.

●       The assumption that each nucleon interacts with the same number of other nucleons is corrected by surface energy. Because this term is negative and proportionate to surface area, it is nearly similar to liquid surface tension.

●       The potential energy of each pair of protons is known as Coulomb energy. The binding energy is lowered because this is a repulsive force.

●       The Pauli exclusion principle is explained by asymmetry energy (also known as Pauli Energy). Uneven quantities of neutrons and protons mean that one type of particle will fill higher energy levels while the other will leave lower energy levels empty.

●       The likelihood for proton and neutron pairs to form is explained by pairing energy. Due to spin coupling, an even number of particles is more stable than an odd number.

Q17) Explain Semi-empirical mass formula.

A17)

B/A, or binding energy per nucleon, is a common representation of binding energy. Because B/A is largely constant, the binding energy is simply proportional to A in general.

However, there are reversals in this pattern. The semi-empirical mass formula captures B/reliance A's on A (and Z). This formula is based on first-principles considerations (a nuclear force model) as well as experimental evidence to determine the specific parameters that define it. All nucleons are uniformly distributed inside a nucleus in this model, known as the liquid-drop model, and are linked together by the nuclear force, whereas the Coulomb interaction causes protons to repel one another. Part of the semi-empirical mass formula is explained by nuclear force (short range) and Coulomb interaction characteristics. Other (smaller) corrections, on the other hand, have been proposed to account for changes in the binding energy that arise due to its quantum-mechanical character (and that give rise to the nuclear shell model).

The semi-empirical mass formula (SEMF) is

M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2

Where the binding energy B(Z, A) is given by the following formula:

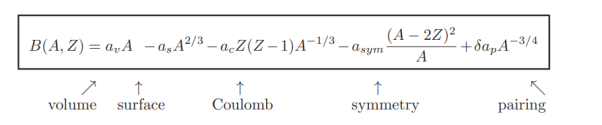
Q18) Write a Short note on Shell Model.

A18)

The Shell Model, for example, accounts for a number of aspects of nuclear energy levels. According to this paradigm, the average attractive force of all the other nucleons governs the mobility of each nucleon. The orbits that arise form "shells," much like the orbits of electrons in atoms. As more nucleons are introduced to the nucleus, they fall into the lowest-energy shells allowed by the Pauli Principle, which stipulates that each nucleon must have its own set of quantum numbers to describe its motion.

.

A nucleus of remarkable stability arises when a shell is full (that is, when the nucleons have used up all of the feasible sets of quantum number assignments). This is comparable to the idea found in an atom, where a filled set of electron quantum numbers produces an atom with extraordinary stability–an inert gas. The number of protons or neutrons in a nucleus is dubbed a "magic number" when all of them are in filled shells. 2, 8, 20, 28, 50, 82, and 126 are some of the magical numbers. The magic number of protons in 116Sn is 50, and the magic number of neutrons in 54Fe is 54. (28). Some nuclei, such as 40Ca and 208Pb, have magical numbers of protons and neutrons; these nuclei are referred to as "doubly magical" because of their unusual stability. On the nuclide chart, magic numbers are indicated.

The total angular momentum, J, of filled shells is zero. The J of the new ground state is determined by the next additional nucleon (a valence nucleon). When nucleons (individually or in pairs) are aroused out of the ground state, their angular momentum, as well as their parity and isospin projection quantum numbers, are altered. The shell model explains how much energy it takes to transfer nucleons from one orbit to the next, as well as how quantum numbers fluctuate. The energy diagram of the two filled shells of the 12C ground state is shown in the diagram above. When a nucleon or a pair of nucleons are promoted to an empty shell, the nucleus enters one of the excited states.

Q19) Difference Between Shell Structure of Nuclei and Shell Structure of Atom.

A19)

Q20) What is History and Origin of the term?

A20)

Maria Goeppert Mayer, a German scientist, became interested in the features of nuclear fission products, such as decay energies and half-lives, while working on the Manhattan Project. She published a body of experimental evidence supporting closed nuclear shells in nuclei with 50 or 82 protons or 50, 82, and 126 neutrons in 1948. (It was already known that nuclei with 20 protons or neutrons were stable; calculations by Hungarian-American physicist Eugene Wigner, one of her Manhattan Project colleagues, demonstrated this.) Two years later, in 1950, she published a second paper in which she blamed spin-orbit coupling for the shell closures at the magic numbers.

According to Maria Goeppert Mayer's student Steven Moszkowski, the word "Wigner coined the phrase "magic number": "Wigner, too, believed in the liquid drop model, but he recognised the very strong evidence for the closed shells from Maria Mayer's work." It appeared to him to be a little like magic, and hence the term 'Magic Numbers' was coined."

These magic numbers formed the foundation of Mayer's nuclear shell model, which he developed with Hans Jensen over the next few years and resulted in their joint Nobel Prize in Physics in 1963.