Unit - 4

Nuclear Physics- II

Q1) Write a short note on Radioactivity and Explain nature of Radioactivity emissions.

A1)

Radioactivity is the property of certain forms of matter to spontaneously emit energy and subatomic particles. It's essentially a property of individual atomic nuclei.

An unstable nucleus will spontaneously dissolve, or decay, into a more stable structure, but only in a few precise ways, for as by generating particular particles or electromagnetic energy. Several naturally occurring elements, as well as artificially manufactured isotopes of the elements, have radioactive decay as a feature. The half-life of a radioactive element is the amount of time it takes for one-half of any given quantity of the isotope to decay. Some nuclei have half-lives of more than 1024 years, while others have half-lives of less than 1023 seconds (see below Rates of radioactive transitions). The daughter of the parent isotope, the outcome of radioactive decay, may be unstable, in which case it will decay as well. The procedure is repeated until a stable nuclide is created.

The nature of radioactive emissions

The alpha () particle, beta () particle, gamma () ray, and neutrino are the most prevalent types of spontaneous radioactive decay emissions. The nucleus of a helium-4 atom, with two positive charges 4/2He, is the alpha particle. Ions are charged atoms that have a positive charge. Two electrons outside the nucleus of a neutral helium atom balance these two charges. Negatively charged (beta minus, sign e) or positively charged (beta plus, symbol e+) beta particles exist. The beta minus [] particle is an electron that is produced in the nucleus during beta decay and has no relation to the atom's orbital electron cloud. The beta plus particle, commonly known as the positron, is the electron's antiparticle; two of these particles will mutually destroy each other when brought together. Electromagnetic radiations such as radio waves, light, and X-rays are examples of gamma rays. The neutrino and antineutrino, particles with no charge and very low mass, are also produced by beta radiation, and are denoted by v and, respectively.

Fission fragments, neutrons, or protons may be emitted in less common kinds of radioactivity. Fission fragments are complex nuclei with a charge Z and mass A that are usually one-third to two-thirds that of the parent nucleus. Neutrons and protons, of course, are the fundamental building components of complex nuclei, with approximately unit mass on the atomic scale and either zero or unit positive charge. The neutron can't stay in the free state for very long. It is quickly grabbed by nuclei in matter; otherwise, it decays to a proton, an electron, and an antineutrino with a half-life of 12.8 minutes in free space. The proton is the stable nucleus of ordinary hydrogen.

Q2) Explain Isomeric transitions.

A2)

For the gamma-emission process, there is a wide range of half-life rates. Dipole transitions (see Gamma transition below), in which the gamma ray carries off one unit of angular momentum, are often quick, taking less than nanoseconds (one nanosecond is 109 second). According to the law of conservation of angular momentum, the total of the angular momenta of the radiation and the daughter nucleus must match the parent's angular momentum (spin). When the spins of the beginning and end states differ by more than one, dipole radiation is prohibited, and gamma emission must take place via a higher multipole (quadrupole, octupole, etc.) gamma transition. The excited nucleus is considered to be in a metastable, or isomeric, state (the terms for a long-lived excited state) if the gamma-emission half-life exceeds around one nanosecond, and the decay is usually classified as another type of radioactivity, an isomeric transition. The protactinium-234 nucleus of the uranium-238 decay chain is an example of isomerism:

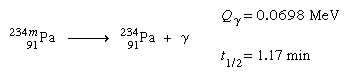
The letter m following the mass number stands for metastable and indicates a nuclear isomer.

Beta-plus decay

New types of radioactivity, beta-plus decay, or positron emission, and electron capture, were discovered among the artificial products of nuclear reactions in the 1930s. In beta-plus decay, an energetic positron is generated and released, along with a neutrino, and the nucleus converts into a daughter with an atomic number one lower but the same mass number. Carbon-11 (Z = 6) decays to boron-11 (Z = 5), one positron, and one neutrino, for example:

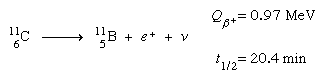
Q3) What is Occurrence of radioactivity?

A3)

On Earth, some types of radioactivity exist naturally. Few species have half-lives comparable to the age of the elements (about 6 109 years), indicating that they did not disintegrate after forming in stars. Uranium-238, uranium-235, and thorium-232 are notable examples. There's also potassium-40, which is the body's primary source of irradiation due to its existence in potassium tissue. Vanadium-50, rubidium-87, indium-115, tellurium-123, lanthanum-138, lutetium-176, and rhenium-187 are beta emitters, while cerium-142, neodymium-144, samarium-147, gadolinium-152, dysprosium-156, hafnium-174, platinum-190, and lead-204 are alpha emitters. Aside from these about 109-year species, there are the shorter-lived daughter activities that are fed by one or more of the above species; for example, various nuclei of the elements between lead (Z = 82) and thorium (Z = 90) are fed by one or more of the above species.

Species formed in the upper atmosphere by cosmic ray bombardment are another type of natural radioactivity. Carbon-14 with a 5,720-year age and 12.3-year tritium (hydrogen-3) with a 53-day age and 2,700,000-year beryllium-10 with a 2,700,000-year age are notable. Small levels of radioactivity have been discovered in meteorites as a result of cosmic ray bombardment throughout their history outside the Earth's atmospheric shield. In fresh meteorite falls, activities as short-lived as 35-day argon-37 have been measured. Since 1945, nuclear explosions have released new radioactivities into the environment, including nuclear fission products as well as secondary products generated by the impact of neutrons from nuclear weapons on nearby matter.

Most of the known beta emitters in the mass range of 75–160 are included in the fission products. They are generated in various yields, peaking at around 7% per fission in the mass regions 92–102 (light peak of the fission yield vs atomic mass curve) and 134–144 (dark peak of the fission yield versus atomic mass curve) (heavy peak). There are two types of radioactivity-related delayed risks. First, fallout falling on Earth raises the overall radiation level. Until the activity has diminished to a suitably low level, protection can be provided by concrete or earth shielding. Second, depending on the half-life, nature of radiations, and chemical behaviour within the body, ingestion or inhalation of even low doses of certain radioactive species can represent a unique threat. See Radiation: Biological Impacts of Ionizing Radiation for further information on the biological effects of radiation.

Nuclear reactors produce fission products as well, but they do so under controlled settings. Containment and waste-disposal procedures should keep operations contained and eliminate the likelihood of leaching into groundwater for periods longer than half-lives. If thermonuclear fusion power can be made feasible, it has a number of advantages over fission power, including not just much bigger fuel stocks (heavy hydrogen and lithium) than uranium, but also the elimination of radioactive fission product wastes. In this context, it's worth noting that radioactive decay is a major source of heat in the interiors of both the Earth and the Moon. These huge heat production sources must be factored into theories concerning the genesis and evolution of the Earth, Moon, and other planets.

Q4) Write a Short note on Stability of nucleus.

A4)

A nucleus is stable if it cannot be changed into a different configuration without the addition of external energy. Only roughly 250 nuclides are stable out of the thousands that exist. The stable isotopes fall into a narrow band when the number of neutrons vs the number of protons for stable nuclei is plotted. The band of stability is the name given to this area (also called the belt, zone, or valley of stability). The straight line in Figure 1 indicates nuclei with a protons-to-neutrons ratio of 1:1. (n:p ratio). It's worth noting that the lighter stable nuclei have an equal amount of protons and neutrons. Nitrogen-14, for example, contains seven protons and seven neutrons. Neutrons are rapidly outnumbering protons in heavier stable nuclei. For example, iron-56 contains 30 neutrons and 26 protons, resulting in a n:p ratio of 1.15, but lead-207 has 125 neutrons and 82 protons, resulting in a n:p ratio of 1.52. This is because larger nuclei have greater proton-proton repulsions, necessitating a larger number of neutrons to compensate for these electrostatic repulsions and hold the nucleus together.

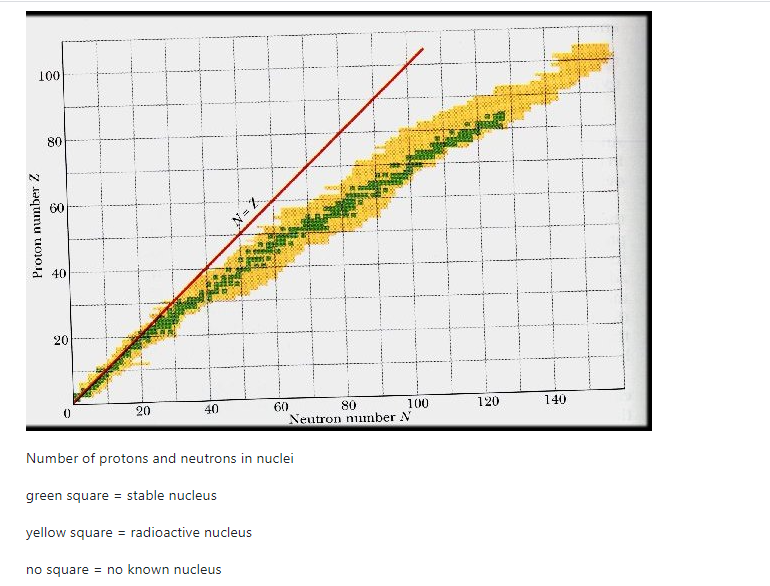
This graph depicts the known nuclides as well as those that are stable. The stable nuclides are coloured blue, whereas the unstable nuclides are coloured green. It's worth noting that all isotopes with atomic numbers greater than 83 are unstable. The solid line is the one on which n equals Z.

The nuclei on the left and right of the band of stability are unstable and produce radioactivity. They decay (transform) into other nuclei that are either within or close to the band of stability. Nuclear decay reactions transform one unstable isotope (or radioisotope) into a more stable isotope. The nature and products of this radioactive decay will be discussed in later sections of this chapter.

Q5) Explain Radioactive decay Law.

A5)

In nature, there are three forms of radioactive decay:

• -decay –emission of a helium nucleus (42He)
• -decay – the emission of electrons or positrons (particles with the same mass as electrons but a charge opposite that of an electron);
• -decay – photons with high energy (hundreds of keV or more) are released.

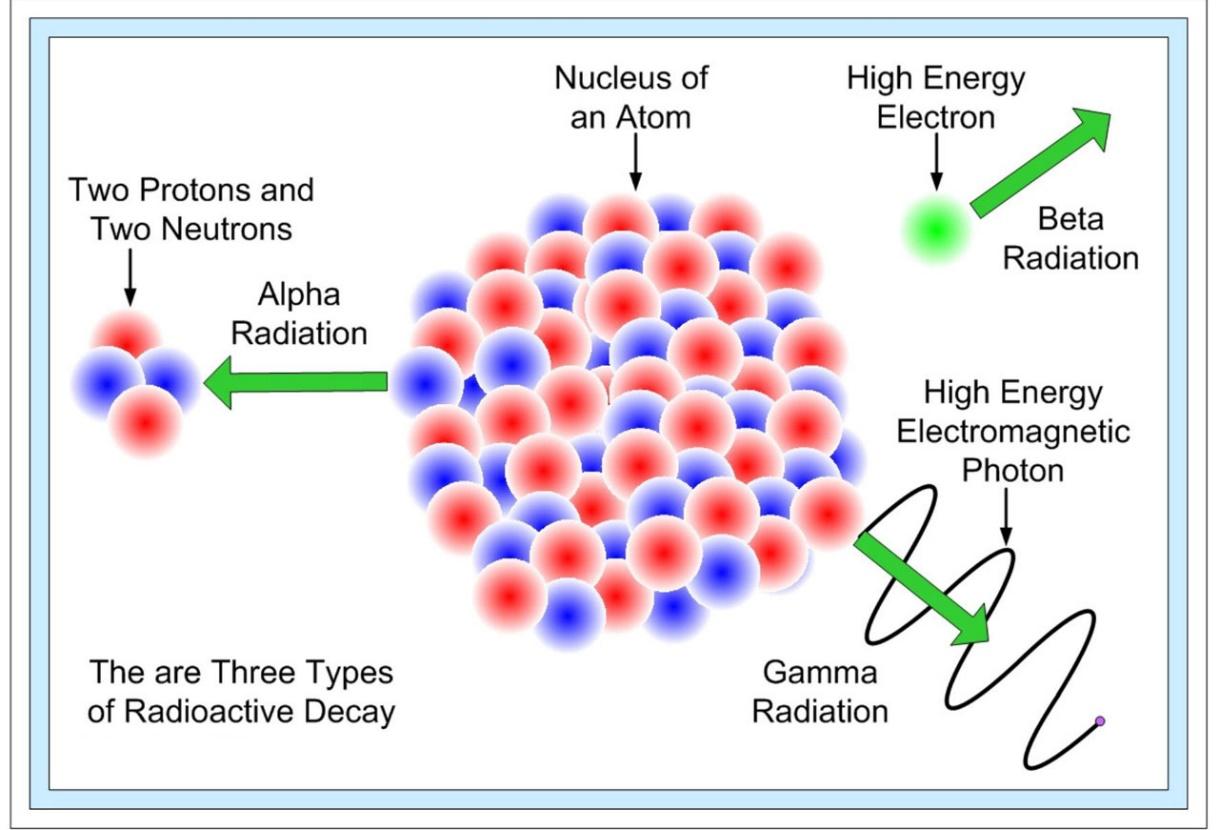
When a radioactive material undergoes α, β or γ-decay, the number of nuclei undergoing the decay, per unit time, is proportional to the total number of nuclei in the sample material. So,

If N = total number of nuclei in the sample and ΔN = number of nuclei that undergo decay in time Δt then,

ΔN/ Δt ∝ N

Or, ΔN/ Δt = λN … (1)

Where λ = radioactive decay constant or disintegration constant. Now, the change in the number of nuclei in the sample is, dN = – ΔN in time Δt. Hence, the rate of change of N (in the limit Δt → 0) is,

DN/dt = – λN

Or, dN/N = – λ dt

Now, integrating both the sides of the above equation, we get,

NN0∫ dN/N = λ tt0∫ dt … (2)

Or, ln N – ln N0 = – λ (t – t0) … (3)

Where, N0 is the number of radioactive nuclei in the sample at some arbitrary time t0 and N is the number of radioactive nuclei at any subsequent time t. Next, we set t0 = 0 and rearrange the above equation (3) to get,

Ln (N/N0) = – λt

Or, N(t) = N0e– λt … (4)

Equation (4) is the Law of Radioactive Decay.

The Decay Rate

In radioactivity calculations, the decay rate R ( = – dN/dt) is more important than the number N. The number of nuclei decaying per unit time is determined by this rate. We can compute the decay rate even if we don't know the amount of nuclei in the sample by counting the number of emissions of, or particles in 10 or 20 seconds. Let's say we take a time interval dt and calculate the decay count N (= –dN). The rate of decay is now defined as,

R = – dN/dt

Differentiating equation (4) on both sides, we get,

R = λ N0 e−λt

Or, R = R0e−λt … (5)

Where, R0 is the radioactive decay rate at the time t = 0, and R is the rate at any subsequent time t. Equation (5) is the alternative form of the Law of Radioactive Decay. Now we can rewrite equation (1) as follows,

R = λN … (6)

Where R and the number of radioactive nuclei that have not yet undergone decay must be evaluated at the same instant.

Q6) What are Half Lives and Mean Lives?

A6)

Specifying the half life or mean life of a process is a way of quantifying how fast it is occurring, when the whole process would in principle take forever to complete.  The example we will talk about here is radioactive growth and decay, but examples from other fields include the recovery of a muscle after some exertion, and the filling of a cistern.

In particular then, the half life of a radioactive element is the time required for half of it to decay (i.e. change into another element, called the "daughter" element).

So if a radioactive element has a half life of one hour, this means that half of it will decay in one hour.  After another hour, half of the remaining material will decay.  But why didn't all of that remaining material decay in that second hour?  Does the element somehow know that it's decaying, and alter its decay speed to suit?

Textbooks are usually content with deriving of the law of decay, and don't tend to address this question.  And yet it forms a classic example of the way in which research in physics (and science in general) is carried out.  Regardless of how we might expect an element to behave—where perhaps the second half might be expected to decay in the same amount of time as the first half—this simply does not happen.  We must search for a theory that predicts this.

Science is often thought to proceed by our logically deducing the laws that govern the world.  But it's not that simple; there are limits to what we can deduce, especially about things in which we cannot directly participate.  Radioactive decay is a good example of this.  We can't use a microscope to watch the events that make an element decay.  The process is quite mysterious.  But what we can do is make a simple theory of how decay might work, and then use that theory to make a prediction of what measurements we can expect.  That's the way science proceeds: by making theories that lead to predictions.  Sometimes these predictions turn out to be wrong.  That's fine: it means we must tinker with the theory, perhaps discard it outright, or maybe realise that it's completely okay under certain limited circumstances.  The hallmark of a good scientific theory is not what it seems to explain, but rather what it predicts.  After all, a theory that says the universe just appeared yesterday, complete with life on earth, fossils and so on, in a sense "explains" everything beautifully by simply defining it to be so; but it predicts absolutely nothing.  So from a scientific point of view it is not a very useful theory, because it contains nothing that allows its truth to be tested.  On the other hand, while it's arguable that the theory of quantum mechanics explains anything at all, it certainly does predict a huge number of different phenomena that have been observed; and that's what makes it a very useful theory.

Q7) Write a Short note on mean life process.

A7)

If half of the atoms in our radioactive element have decayed after one half life, we can expect some form of well-defined average life expectancy: the atoms' mean life, which is slightly greater than their half life. The half life is equal to the natural logarithm of 2 divided by the mean life (about 0.693). The time constant, which appears in the exponential term et/ associated in defining decay or growth, turns out to be exactly equal to the mean life. The term "time constant" refers to the fact that the mean life equals; the fact that the mean life equals is a nice coincidence that allows us to think about the mean life in the following, alternate way.

As previously stated, the time it takes for the remaining amount of the element to decline to a half, a third, or any fraction at all can be used to represent the speed of any decay process. One unusual choice of that number is e, and the time it takes for the remaining amount to be reduced to 1/e of the original also happens to be the decay's mean life. One of the reasons why the number e is so significant is because of this. Aside from having pleasant qualities that make the mathematics of growth and decay easier to understand, e quantifies ordinary concepts like the average life expectancy of atoms.

When we plot the amount of a radioactive element as a function of time, we see that it decreases with a typical "exponential decay curve," which helps to mathematically demonstrate the half-life concept. Here's a question for you: Assume the element did not decay exponentially (i.e. with a half life), but rather linearly, with the rate of decay always equal to the original rate (resulting in a simple "first half in one minute, second half in the next minute—and then, all gone" scenario). How long would it take to entirely evaporate in such an idealised scenario? Assume we have 1000 atoms of a radioactive material, with 10 atoms decaying each second at the start. How long would it take to entirely evaporate if it continued to degrade at this rate (it won't, but pretend it did)? Of course, the answer is 100 seconds. It has now been discovered that this is exactly equal to the mean life of the real element.  (Which means that we know straight away that the real element's half life is 69.3 seconds.)

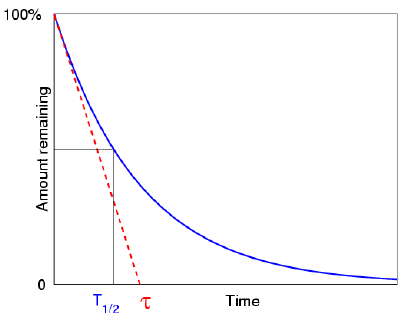
This way of looking at the concept of mean life also appeals to our intuition: it

According to this theory, if atoms behaved in the lovely, linear way that we humans enjoy thinking about them, the time it would take for them all to decay would be exactly equal to the mean life of the actual, real-world element. You can see how the number e is linked to basic linearity concepts, which is one of the reasons why it is such a powerful number in mathematical analysis.

Q8) Explain the Types of Beta Decay.

A8)

Beta decay can be divided into three categories. The “ordinary” beta decay, also known as decay or electron emission, was the first to be found. In nuclear beta decay, the symbol symbolises an electron emitted. The nuclide cobalt-60 decays in the following manner: 60Co 60Ni + neutrino.

The neutrino is an unforeseen particle emitted during beta decay that is extremely important. The neutrino was not even hypothesised in theory until more than 20 years after electron emissions were discovered in beta decay. Neutrinos are so difficult to detect that it took until 1953 to gain the first direct proof of them. Neutrinos have almost no mass, no charge, and do not interact with nucleons through the strong nuclear interaction. Because they are travelling at nearly the speed of light, they have very little time to influence any nucleus they come across. This is because they don't interact through the EM force because they don't have any charge (and aren't EM waves). They do interact via the weak nuclear force, which is relatively weak and has a very short range. As a result, neutrinos can get through practically any detector and through practically any shielding. Neutrinos, on the other hand, carry energy, angular momentum (as fermions with half-integral spin), and linear momentum away from beta decay. When precise beta decay measurements were made, it became clear that the daughter nucleus and electron could not account for all of the energy, angular momentum, and linear momentum. Either they were being carried away by an unknown particle or three conservation rules were being broken. In 1930, Wolfgang Pauli proposed the existence of neutrinos in a formal paper. When he devised a detailed theory of beta decay, the Italian-born American scientist Enrico Fermi (1901–1954) gave neutrinos their name, which means "little neutral ones" (see Figure 3). The identification of the weak nuclear force as separate from the strong nuclear force, and hence responsible for beta decay, was part of Fermi's theory.

A new conservation law is also revealed by the neutrino. The electron family is one of the many different types of particles. In any process or closed system, we argue that the number of members of the electron family is constant. There are no members of the electron family present before the decay in our example of beta decay, but there is an electron and a neutrino afterward. As a result, electrons are assigned a +1 electron family number. The antineutrino of an electron in decay is given the symbol ve e, where nu is the Greek letter and the subscript e indicates that this neutrino is connected to the electron. This is an antimatter particle, as indicated by the bar. (Antimatter counterparts are almost identical to matter counterparts except that they have the opposite charge.) On Earth, antimatter is nearly absent, though it can be discovered in nuclear decay and other nuclear and particle reactions, as well as in outer space.) Because the electron is antimatter, its antineutrino e e has an electron family number of –1. Before and after the decay, the total is zero. The total electron family number is constant, according to the new conservation law, which must be followed in all circumstances. It is impossible to generate an electron without also creating an antimatter family member. In a scenario where total charge is initially zero and equal amounts of positive and negative charge must be formed in a reaction to keep the total zero, this law is equivalent to the conservation of charge.

Q9) Explain Pauli’s Idea of the Neutrino.

A9)

Pauli's suggestion was an attempt to solve a difficult experimental challenge that had piqued the physics community's interest for several years. Ellis and Wooster published an experiment in 1927 that demonstrated that the electrons emitted in radioactive decay had a broad and continuous range of energy. This perplexing finding not only shattered the analogy with -decay, in which the energy of the emitted -particles was calculated for each potential -decay, but it also sparked some strange speculations. For example, Rutherford and Chadwick proposed that not all nuclei of a certain -unstable element were identical because they had various internal energies, and Bohr proposed that energy is not conserved in decay, allowing electrons to escape with a variety of energies. 13 This was hardly the only concern with nuclear research at the time. The tests in 1926 that demonstrated that nitrogen nuclei behaved according to BoseEinstein statistics revealed yet another major flaw in nuclear theory and the p-e model. According to the latter, because both protons and electrons have spin 12, nitrogen (atomic mass 14 and nuclear charge 7) should have a half-integer total spin. This suggests that nitrogen nuclei should follow Fermi-Dirac statistics if the p-e model is correct. The observed Bose-Einstein statistics, however, required that the nucleus comprised of an even number of half-integer particles, adding up to an integer total, which is required to explain these statistics. In 1929, Pauli was introduced to these challenges by Bohr, who was considering a restriction of the concept of energy conservation to solve these problems, a concept that Pauli found to be "very little satisfaction" (according to a letter to Bohr reprinted in Peierls 1986, p. 5). As Bohr and his partners continued down this route of energy nonconservation, Pauli began to consider another notion, which he first articulated in December 1930. Let us begin, like we did with Rutherford, by attempting to comprehend Pauli's perspective and models on the subject. We can next discuss how he changed Rutherford's concept to suit his own needs. Pauli, like his contemporaries, viewed radioactive decay as a reaction in which an unstable nucleus (as in the previous instance) disintegrated spontaneously into a residual nucleus, with the observed emitted - or -particle plus some -radiation (the situation afterwards). The model of this reaction preserves both energy and electric charge for -particles, but the unexplainable continuity of energies in the situation afterward has led some to believe that this continuity already existed in the situation before (Rutherford and Chadwick), or to suggest that the energy conservation constraint for this model be retracted (Bohr). This final proposal was what prompted Pauli to address the issue. We need to look at some of his objections to see why he was so opposed to Bohr's views. Bohr's notion to keep charge conservation but renounce energy conservation in -decay is challenged in a letter to Klein, a close associate of Bohr, by the following thought experiment: 13 Gauderis 2013 provides a thorough examination of this puzzle and all proposed possibilities. “Imagine a sealed chamber filled with radioactive decay. [...]... If the energy law were not applicable for -decay, the overall weight of the closed box would change as a result. This contradicts my understanding of physics! For then, even the gravitational field – which is generated [...] by the complete box (including the radioactive content) – must be expected to change, whereas the electrostatic field, [...], should remain unchanged due to charge conservation.” Jensen 2000, p. 153) (reprinted in Jensen 2000, p. 153) Pauli's main critique is that the field formalisms for gravity and electrostatics, which both rely on inverse-square laws, are built similarly and hence regarded to be of the same kind. Bohr's suggestion, by breaking this analogy, has the far-reaching consequence of undermining the physical concept of a field. Unlike most quantum theorists, who rarely dealt with gravity, 14 Pauli was a specialist in general relativity. 15 As a result, Pauli, unlike other nuclear physicists, was far more cognizant of field structures as the basic ontological ideas for physical reality. This explains why Bohr's theories bothered him so much. If Pauli was confident that conservation principles must apply in this reaction model, it occurred to him quickly that the only way to balance the disequilibrium between the before and after states was to add something to the picture. However, nothing new has been discovered in the -decay experiments thus far. As a result, he wanted to find something that was either unobservable or extremely difficult to observe. Because the law of conservation of electrical charge was already in effect, it had to be electrically neutral as well. In other words, his reaction model for the -decay process had a gap that needed to be filled by an idea or object that has these two traits.

Q10) Explain Nuclear Fission.

A10)

Fission occurs when a nucleus splits, releasing free neutrons and lighter nuclei. Heavy element fission is very exothermic, releasing roughly 200 million eV compared to coal combustion, which produces only a few eV. Because only 0.1 percent of the original nuclei are converted to energy, the quantity of energy released during nuclear fission is millions of times more efficient per mass than coal. As a result of the reaction, a daughter nucleus, energy, and particles such as neutrons are emitted. The released particles can then react with other radioactive materials, resulting in the production of daughter nuclei and more particles, and so on. Nuclear fission reactions are unique in that they can be harnessed and exploited in chain reactions. Nuclear weapons are built on this chain reaction. U235U235 is a well-known element utilised in nuclear fission that, when hit with a neutron, transforms into U236U236 which is even more unstable and splits into daughter nuclei such as Krypton-92 and Barium-141, as well as free neutrons. The fission products that occur are highly radioactive and frequently decay.

Nuclear fission occurs when the nucleus of an atom splits into nuclei of lighter atoms, releasing energy as a result of a neutron bombardment. Enrico Femi proposed the idea of nuclei splitting in 1934, believing that transuranium elements may be created by bombarding uranium with neutrons, because the loss of Beta particles would increase the atomic number. However, the properties of elements with greater atomic numbers than uranium did not coincide with the products that formed (Ra, Ac, Th, and Pa). They were instead radioisotopes of much lighter elements like Sr and Ba. The quantity of mass lost in the fission process is equal to 3.201011J3.201011J of energy.

Q11) Explain Nuclear Fusion.

A11)

The combining of two nuclei to generate a heavier nucleus is known as nuclear fusion. Energy is released or absorbed as a result of the reaction. Fusion of nuclei with lower mass than iron produces energy, whereas fusion of nuclei with higher mass absorbs it. Iron peak is the name given to this phenomena. Nuclear fission, on the other hand, has the opposite effect.

The energy generated from the sun and many other stars in the universe is driven by the power of the energy in a fusion process. Nuclear fusion is also used in nuclear weapons, namely the hydrogen bomb. Nuclear fusion is an energy-producing process that occurs at extremely high temperatures, such as those found in stars like the sun, when smaller nuclei are fused together to form a larger nucleus, releasing massive amounts of heat and radiation in the process. When left uncontrolled, this process can generate nearly infinite amounts of energy, and an unregulated chain can form the basis for a hydrogen bond, since hydrogen is regularly fused. This thermonuclear reaction is also fueled by the combining of deuterium atoms to generate helium atoms. Consider the following scenario:

H12+H13→He24+n01+energy(12)(12)H12+H13→He24+n01+energy

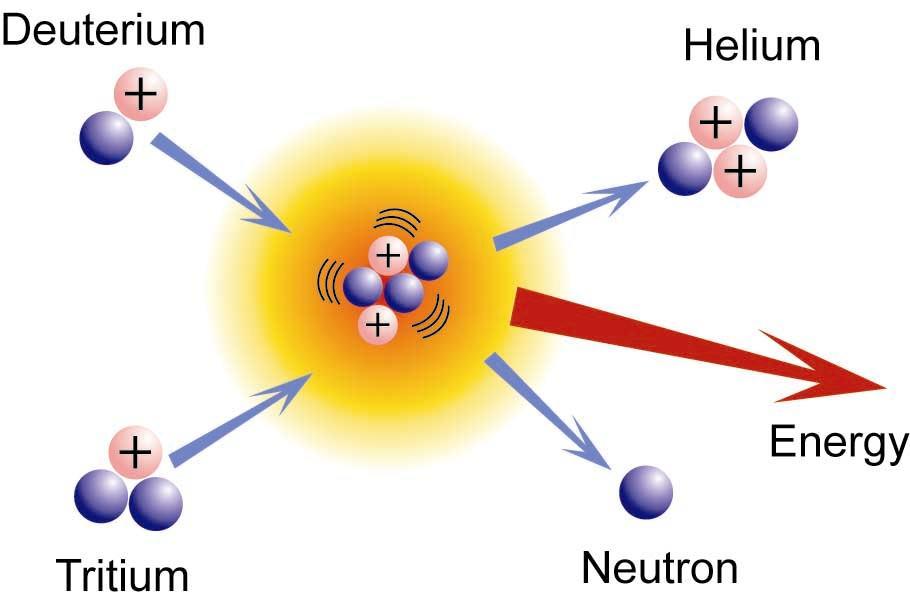
The difficulty of bringing deuterium and tritium nuclei into close contact, achieving high enough thermal energy, and thoroughly ionising gases into plasma are all issues that have yet to be thoroughly shown in a controlled fusion reaction.

Q12) What is Generation of Energy?

A12)

E=mc2 (16.2.1)

In this equation, E denotes energy, mm denotes mass, and cc denotes the speed of light (31083108 metres per second), which is the constant that connects the two. Because mass is a measure of matter quantity, the importance of this equation is that matter can be turned into energy and vice versa. Let's compare this equation for converting matter and energy to some other similar conversion equations:

Inches = feet×12inches = feet×12

Or

Cents = dollars×100cents = dollars×100

When we convert matter into energy, we consider how much mass the matter has, just as any conversion formula allows you to compute the conversion of one item into another. In this situation, the conversion factor is neither 12 or 100, as in our previous instances, but another constant quantity: the speed of light squared. It's worth noting that this conversion doesn't require matter to travel at the speed of light (or the speed of light squared). The c2c2 factor is just the number that Einstein demonstrated must be used to connect mass and energy.

It's worth noting that this formula doesn't tell us how to convert mass to energy, much like the cents formula doesn't tell us where to swap coins for a dollar note. The formulas simply tell us what the corresponding numbers are if the conversion is successful. No one had any notion how to turn mass into energy in any practical sense when Einstein initially developed his formula in 1905. Einstein himself tried to dispel the notion that large-scale atomic mass to energy conversion would be possible in the near future. We regularly turn mass into energy in power plants, nuclear weapons, and high-energy physics experiments in particle accelerators nowadays as a result of advances in nuclear physics.

Because the speed of light squared (c2c2) is such a huge number, even a small amount of mass is converted into a big amount of energy. For example, converting 1 gramme of matter (about 1/28 ounce, or about 1 paperclip) to energy equivalent to burning 15,000 barrels of oil would yield the same amount of energy.

Scientists rapidly understood that the Sun's heat and light come from the conversion of mass into energy. The amount of energy radiated by the Sun could be produced by the complete conversion of nearly 4 million tonnes of matter into energy inside the Sun every second, according to Einstein's E=mc2E=mc2 equation. When compared to terrestrial objects, destroying 4 million tonnes every second may seem like a lot, but keep in mind that the Sun is a massive storehouse of matter. We will see that the Sun has more than enough mass to annihilate such massive amounts of matter while still blazing at its current rate for billions of years.

Q13) Write a Short note on Special relativity.

A13)

Special relativity is a theory of spacetime structure. It was first mentioned in Einstein's paper "On the Electrodynamics of Moving Bodies" published in 1905. (for the contributions of many other physicists see History of special relativity). Special relativity is founded on two contradicting postulates in classical mechanics:

1. For all observers in any inertial frame of reference relative to one another, the rules of physics are the same (principle of relativity).

2. Regardless of their relative mobility or the velocity of the light source, the speed of light in a vacuum is the same for all observers.

The resulting theory outperforms classical mechanics in terms of experimentation. For example, postulate 2 explains the Michelson–Morley experiment results. Furthermore, the theory has a number of unexpected and paradoxical ramifications. Here are a few examples:

If the observers are in relative motion, two events that are contemporaneous for one observer may not be simultaneous for another observer.

Time dilation refers to the fact that moving clocks tick more slowly than a "stationary" clock.

Objects are measured to be shortened in the direction that they are travelling with regard to the observer in length contraction.

The maximum speed is limited: in a vacuum, no physical item, communication, or field line can travel faster than the speed of light.

o Gravitational forces can only travel through space at the speed of light, not faster or instantly.

Equivalence of mass and energy: E = mc2, energy and mass are equivalent and interchangeable.

Some researchers use the term "relativistic mass."

[nine]

The Lorentz transformations replace the Galilean transformations of classical mechanics as the distinguishing feature of special relativity. (See Maxwell's electromagnetic equations.)

Q14) Give Introduction about general relativity.

A14)

General relativity is a gravitational theory developed by Albert Einstein between 1907 and 1915. The equivalence principle, which asserts that accelerated motion and being at rest in a gravitational field (for example, when standing on the surface of the Earth) are physically equal, was the foundation of general relativity. As a result, free fall is inertial motion: an item in free fall is falling because that is how objects move when no force is applied to them, rather than due to the force of gravity, as is the case in classical mechanics. This contradicts classical mechanics and special relativity, which state that inertially moving objects cannot accelerate with regard to one another, yet free-falling objects may. Einstein argued that spacetime is curved to overcome this problem. He developed the Einstein field equations in 1915, which relate the curvature of spacetime to the mass, energy, and momentum contained inside it.

Gravity time dilation: Clocks run slower in deeper gravitational wells, as a result of general relativity. [nine]

●        Precession: In Newton's theory of gravity, orbits precess in an unexpected fashion. (This has been detected in Mercury's orbit as well as binary pulsars.)

●        Light deflection occurs when light rays bend due to a gravitational field.

●        Rotating masses "pull" the spacetime around them, which is known as frame-dragging.

●        The cosmos is expanding metrically, and the distant reaches of it are moving away from us faster than the speed of light.

●        General relativity is a gravitational theory that uses the Einstein field equations as its defining feature. The field equations' solutions are metric tensors, which determine the topology of spacetime and how inertial objects move.

Q15) Give 1 Example of Calculating Energy Released By Fission.

A15)

Calculate the energy released in the following spontaneous fission reaction:

238U → 95Sr + 140Xe + 3n

Given the atomic masses to be m(238U) = 238.050784 u, m(95Sr) = 94.919388 u, m(140Xe) = 139.921610 u, and m(n) =1.008665 u.

Strategy

As always, the energy released is equal to the mass destroyed times c2, so we must find the difference in mass between the parent 238U and the fission products.

Solution

The products have a total mass of

Mproducts=94.919388 u+139.921610 u+3(1.008665 u)=237.866993 u

The mass lost is the mass of 238U minus mproducts, or

Δm = 238.050784 u− 237.8669933 u = 0.183791 u,

So the energy released is

E=(Δm)c2=(0.183791 u)931.5 MeV/c2uc2=171.2 MeV

Q16) What is Nuclear reactor?

A16)

The energy of neutrons produced by fission events diminishes on the order of a few electronvolts or fractions of an electronvolt after a series of encounters with different nuclei. Neutrons with energy in this range are said to as'slow,' whereas neutrons with energy that match those of the surrounding atoms are referred to as 'thermal.'

These slow neutrons enable nuclear reactors to run on natural uranium or uranium that has been lightly enriched in fissile isotope 235 as fuel. The most prevalent pressurised (PWR) and boiling water (BWR) reactors would not function without them. As a result, collisions within a medium termed a moderator must slow down the neutrons released by nuclear fission. Reactors using natural uranium fuel, which contains only 0.7% fissile uranium 235, require efficient moderators that absorb extremely few neutrons: heavy water and pure graphite are examples of such moderators.

Q17) Write a Short note on Slow neutrons favour fission.

A17)

Slow neutrons are neutrons that have slowed down after colliding with atomic nuclei in nuclear reactors. The kinetic energy of these particles is on the order of a few electronvolts or a fraction of an electronvolt(eV). The neutron is said to be thermal when its energy is equivalent to the kinetic energies of the atoms in the medium through which it travels.

It's possible that the word "slow" is a misnomer. A thermal neutron with a charge of 0,025 electronvolts travels at a speed of 2 km/sec, quicker than the fastest airliner. However, compared to the speed of light, 2 km/sec is a snail's pace. The kinetic energy of the neutron is more important than its speed.

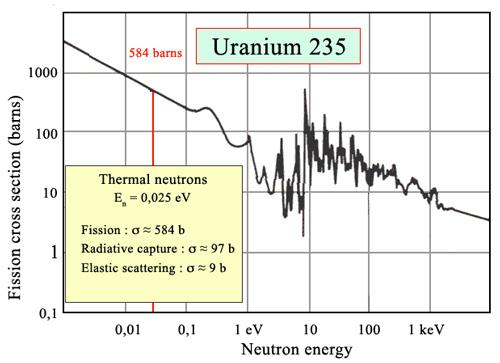
Fig. Uranium-235 fission probability

The chance of fission, also known as the fission cross-section by physicists, varies dramatically with neutron intensity. Barns are used to measure it. This fission probability is highest for a fissile nucleus like uranium-235 at kinetic energy of a few electronvolts. Because the fraction of uranium-235 in most reactor fuels is only a few percent, it is necessary to compensate for this low proportion by increasing the fission probability of Uranium-235, and hence operate with a sluggish neutron flow.

Q18) Explain Fusion reactions in stars.

A18)

Stars' principal energy source and the process for the nucleosynthesis of light elements are fusion processes. Hans Bethe discovered in the late 1930s that the fusion of hydrogen nuclei to generate deuterium is exoergic (i.e., there is a net release of energy) and leads to the synthesis of helium when combined with subsequent nuclear processes. Helium production is the primary source of energy emitted by ordinary stars like the Sun, whose burning-core plasma has a temperature of less than 15,000,000 K. However, because the gas that forms a star often contains certain heavier elements, like as carbon (C) and nitrogen (N), nuclear interactions between protons and these nuclei are vital to consider. The proton-proton cycle is the reaction chain between protons that eventually leads to helium. When protons also cause carbon and nitrogen to burn, the CN cycle must be taken into account; and when oxygen (O) is added, the CNO bi-cycle must also be taken into account. (For further information, see the carbon cycle.)

In a hydrogen-only star, the proton-proton nuclear fusion cycle begins with the reactionH + H D + + + v; Q = 1.44 MeV, where the Q-value assumes positron annihilation by an electron. Although deuterium can combine with other deuterium nuclei, the D/H ratio is kept low, typically 1018, due to the abundance of hydrogen. As a result, the following phase isH + D 3He +; Q = 5.49 MeV, where shows that some of the energy output is carried away by gamma rays. The last stage in the chain, the burning of the helium-3 isotope, produces ordinary helium and hydrogen: 3He + 3He 4He + 2(H); Q = 12.86 MeV.

Because its reaction rate with hydrogen is minimal, helium-3 burns mostly by reactions with itself at equilibrium, while burning with deuterium is minimal due to the low deuterium concentration. If the temperature is greater than roughly 10,000,000 K, reactions with helium-3 can result in the creation of still-heavier elements such as beryllium-7, beryllium-8, lithium-7, and boron-8.

Q19) What is Cold fusion and bubble fusion?

A19)

There are two controversial fusion experiments worth mentioning. Martin Fleischmann of the University of Utah and Stanley Pons of the University of Southampton in England claimed in 1989 that they had successfully created fusion reactions at virtually room temperature. Electrolytic cells holding heavy water (deuterium oxide, D2O) and palladium rods that absorbed the deuterium from the heavy water comprised their system. Attempts to provide a theoretical explanation for the data, as well as worldwide efforts to replicate the purported cold fusion, were unsuccessful.

During acoustic cavitation experiments with chilled deuterated (bombarded with deuterium) acetone in 2002, Rusi Taleyar khan and colleagues at Purdue University in Lafayette, Indiana, claimed to have observed a statistically significant increase in nuclear emissions of products of fusion reactions (neutrons and tritium). Their setup was inspired by the well-known phenomena of sonoluminescence. A gas bubble is burst with high-pressure sound waves in sonoluminescence. Conditions of high density and temperature are obtained at the end of the implosion process, and for a short time following, resulting in light emission. The researchers claimed to have created densities and temperatures sufficient to cause fusion reactions just before the bubbles split up by starting with larger, millimetre-sized cavitations (bubbles) that had been deuterated in the acetone liquid. Most attempts to reproduce these outcomes, including cold fusion, have failed.

Q20) What is Stellar thermostat?

A20)

Both the p-p chain and the CNO cycle operate as stellar thermostats because they are so sensitive to temperature variations. Changes in the pace of energy generation can lead the gas layers above the core to expand outwards or contract inwards, depending on the rate of energy generation. However, the high temperatures required for fusion reactions are produced by the gravitational pressure of these overlying layers of gas. As a result, there is a delicate balance that tends to return to its original state.

Energy pushing OUT balances gravity pulling IN at Equilibrium Temp.

If the temperature in the centre of the building lowers,

o Energy production declines.

As a result, the amount of gas pushing outwards lowers...

As a result, gravity pulls the outer layers inwards.

It appears bleak... But as the outer layers press the core within, the situation improves.

o The centre temperature returns to its original level...

As a result, fusion rates rise...

As a result, more energy is created...

As a result, the gas pressure pushing outwards rises...

o resulting in the outer layers returning to their previous position

You can demonstrate that if the central temperature raises slightly for some reason, a similar set of activities will cause the core to expand slightly, causing the temperature to decrease back to its original amount.

In short, a stable equilibrium is achieved when the energy released by fusion events pushes outwards and the gravitational force pulls gas inside. A star will keep a nearly constant central temperature as long as it has hydrogen in its core to fuse, which means it will generate an approximately constant quantity of energy, which means it will shine with a nearly constant luminosity. During its long phase of hydrogen burning, its location on the HR diagram (based on luminosity and photosphere temperature) won't vary significantly.