Unit - 1
Complex Analysis
Q1) Define Complex, Real and Imaginary number in mathematics.
A1)
Complex number
A complex number is a number that is made up of both real and imaginary numbers. The complex number is in the form of a+ib, where a = real number and ib = imaginary number. In addition, a,b are real values, and I = -1.
Hence, a complex number is a simple representation of addition of two numbers, i.e., real number and an imaginary number. One side is entirely genuine, while the other is entirely imagined.
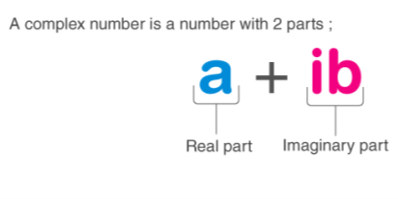
Real Numbers
Real numbers are any numbers that exist in a number system, such as positive, negative, zero, integer, rational, irrational, fractions, and so on. Re is the symbol for it (). 12, -45, 0, 1/7, 2.8, 5, and other real numbers are examples.
Imaginary Numbers
Imaginary numbers are numbers that are not real. We get a negative return when we square an imaginary number. Im is the symbol for it (). For example, the numbers -2, -7, and 11 are all fictional.
To answer the equation x2+1 = 0, complex numbers were introduced. The equation's roots are of the form x = -1, and there are no true roots. As a result of the addition of complex numbers, we now have imaginary roots.
The symbol I which stands for Iota, is used to represent -1. (Imaginary number).
Q2) What is Representation of Z modulus on Argand Plane?
A2)
Argand plane consists of real axis (x – axis) and imaginary axis (y – axis).
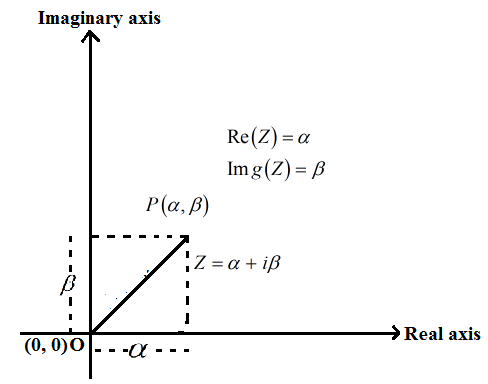
|Z| = √(α – 0)2 + (β – 0)2
= √(α )2 + (β)2
= √Re (z )2 + Img (z)2
|z| = | α + iβ| = √(α )2 + (β)2
Q3) What is Conjugate of Complex Numbers on argand plane?
A3)
A complex number's conjugate is a number with the same real portion and the opposite sign of the imaginary portion but identical magnitude.
The complex number Z = + I will be used.
The conjugate of a particular complex number will be represented as the mirror image of Z = + I along the real axis.
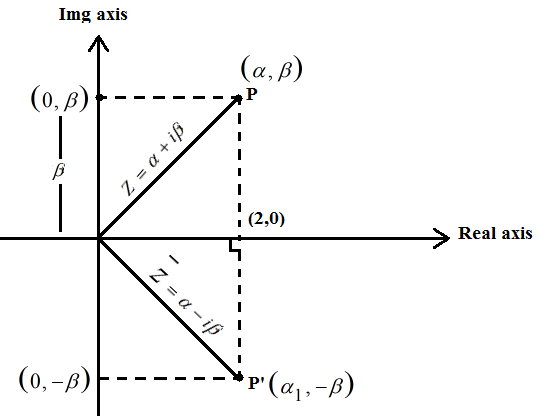
Z = α + iβ (complex number)
 (conjugate of complex number)
(conjugate of complex number)
Q4) Explain Distance Between Two Points in Complex Plane.
A4)
In the argand plane, if two complex integers Z1 and Z2 are labelled as P and Q, respectively, the distance between P and Q is given as.
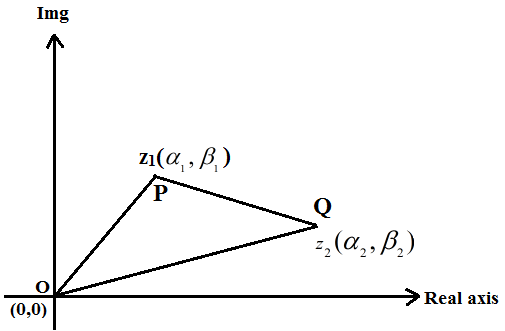
PQ = |z2 – z1| = |(α2 – α1) + i(β2 – β1)| = √( α2 – α1)2 + (β2 – β1)2
For example, Find the distance of a point P, Z = (3 + 4i) from origin.
Solution:
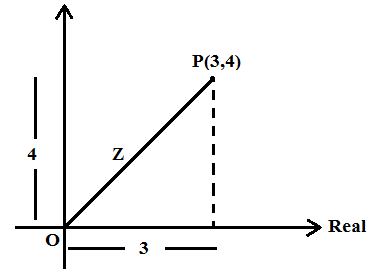
|Z| = |3 + 4i|
= √ 32 + 42 = 5 units
Q5) Write a Short note on Polar form of Complex number.
A5)
Both rectangular and polar coordinates can be used to represent complex values. We'll look at the polar form of any complex number here.
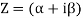
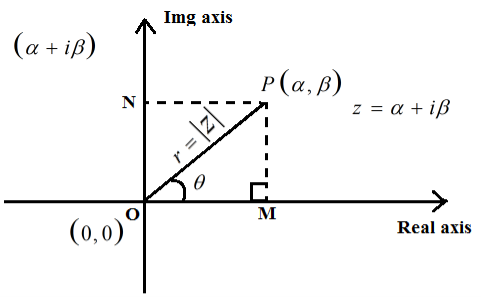
Z = α + iβ, |z| = r
OM = r cos θ = α
ON = r sin θ = β
Hence, Z = α + iβ
= (OM) + i (ON)
= r cos θ + i r sin θ = r( cos θ + i sin θ) r = 
Where ‘' stands for complex number argument.
θ = arg (z)
For a complex number's conjugate
Arg (
Q6) Explain Product of two Complex number.
A6)
Let P and Q represent complex number
Z1=(α1+iβ1) and
Z2=(α2+iβ2) in argand plane
θ1=arg(z1),
θ2=arg(z2) (given)
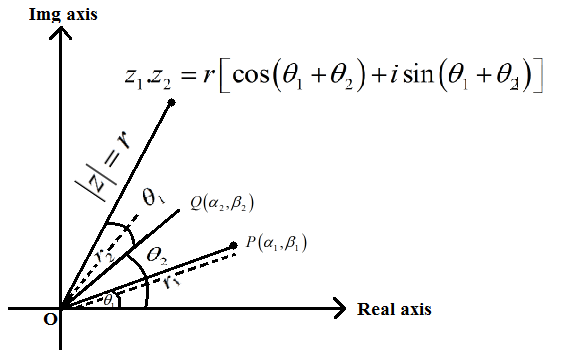
Now, on multiplying Z1 Z2 = Z
Z = ( α1 + i β1) ( α2 + i β2) = r1 ( cos θ1 + i sin θ1). r2 ( cos θ2 + i sin θ2)=
r1r2[ cos(θ1 + θ2) + i sin (θ1 + θ2)]
Let say r1. r2 = r
Z = r( cos(θ1 + θ2) + i sin (θ1 + θ2))
Q7) Explain Derivation 1: Power Series in Details.
A7)
The use of power series is one of the more intuitive derivations of Euler's formula. It entails expanding the exponential, sine, and cosine power series to arrive at the conclusion that the equivalence holds.
As a precaution, this method presupposes that the sinz, cosz, and ez power series expansions are perfectly convergent everywhere (e.g., that they hold for all complex numbers z). It does, however, have the advantage of demonstrating that Euler's formula holds for all complex numbers z.
The power series expansion of ez for a complex variable z is
ez = 1 + z/ 1! + z2/2! + z3/3! + z4/4! + . . .
Let's pretend that z is ix (where x is an arbitrary complex number). I am raised to greater powers as z is raised to greater abilities. The first eight powers of I are as follows:
i0 = 1 i4 = i2 . i2 = 1
i1 = i i5 = i . i4 =i
i2 = 1 (by the definition of i) i6 = i . i5 = -1
i3 = i . i2 = - i i7 = i . i6 = -i
(Notice how the powers of I are cyclical: 1, I 1, i. We'll be putting these abilities to good use soon.)
When z=ix, the expansion of ez is as follows:
eix = 1 + ix + (ix)2/2! + (ix)3/3! + (ix)4/4! + . . .
We get the following results when we extract the powers of I
eix = 1 + ix - (ix)2/2! - (ix)3/3! + (ix)4/4! + (ix)5/5! - (ix)6/6! - (ix)7/7! + (ix)8/8! +. . .
We can rearrange the terms of ez's power series expansion without changing its value because it is totally convergent. The result of combining the real and imaginary terms is
eix = (1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .) + i (x – x3/3! + x5/5! – x7/7! +. . .)
Let's take a detour and look at the sine and cosine power series. The cos x power series is
Cos x = 1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .
And for sinx, it is
Sin x = x – x3/3! + x5/5! – x7/7! +. . .
To put it another way, the last equation we had was exact.
eix = cos x + i sin x
This is the Euler's formula statement we were seeking for.
Q8) Give the Applications Of Complex Numbers.
A8)
Euler's formula, as one of the most important equations in mathematics, has a plethora of interesting applications in a variety of fields. These include, for example:
- The famous Euler's identity The exponential form of complex numbers Trigonometric and hyperbolic functions with different meanings
- Exponential and logarithmic functions are generalised to complex numbers.
- De Moivre's theorem alternate proofs and trigonometric additive identities
- Euler's Personality
- Euler's identity is frequently regarded as mathematics' most beautiful equation. It's written like this:
- Ei+1=0 ei+1=0 ei+1=0 ei
- Where five of the most essential constants in mathematics are highlighted. These are the following:
- The identity of addition 0
- The unity number one
- The Pi constant (circumference to diameter ratio) is a mathematical constant.
- e is the natural logarithm's base.
- The fictitious unit I
Q9) What is De Moivre’s theorem?
A9)
De Moivre's theorem establishes a formula for computing complex number powers. Consider what occurs when we multiply a complex number by itself to obtain some idea for de Moivre's theorem.
Remember that any complex number z=a+ib can be expressed as with the polar form.
Then squaring the complex number z gives
z2 =(r( cos θ + i sin θ))2
= r2( cos θ + i sin θ)2
= r2( cos θ cos θ + i sin θ cos θ + i sin θ cos θ + i2 sin θ sin θ)
= r2((cos θ cos θ – sin θ sin θ) + i(sin θ cos θ + sin θ cos θ))
= r2(cos 2 θ + i sin 2 θ)
This demonstrates that squaring a complex integer squares the absolute value and multiplies the argument by two. For n3, de Moivre's theorem shows that to increase a complex number to the nth power, the absolute value must be raised to the nth power, and the argument must be multiplied by n.
Q10) Write a Short note Roots of Complex Numbers.
A10)
Let z be a complex number that is not zero. Then in C, there are exactly k many kth roots of z.
Assume that w is a complex number. We want to identify all z such that zn=w, or the nth roots of w.
There are n different nth roots, which can be discovered in the following order:.
- Write z and w in polar form as z=rei,w=sei. Zn=w then becomes:
(reiθ)n = rneinθ = seiϕ
We need to solve for r and θ.
2. Solve the following two equations:
rn=s
einθ=eiϕ
3. The solutions to rn=s are given by r= .
.
4. The solutions to einθ=eiϕ are given by
nθ = ϕ + 2 πl, for l = 0, 1, 2, . . ., n - 1
Or
θ = ϕ/n + 2/n πl, for l = 0, 1, 2, . . . , n -1
5. Using the solutions r,θ to the equations given in construct the nth roots of the form z=reiθ.
Q11) What is Logarithm functions?
A11)
Because a complex number can be expressed as an exponential function, reiP , A logarithm is nearly instantaneous. We get it. Ln reiP = ln r + ln eiP = ln r + iP , This is the natural logarithm's primary value. The angle PP, on the other hand, is not unique, as it can vary by multiples of two. As a result, the formula for a complex number's natural logarithm is ln reiP = ln r + iP + 2kπi
We can find the natural logarithm of I for example. Its main benefit is
Ln i = ln (1 eiπ/2) = π/2 i
The natural logarithm of negative one is another fascinating example. Its main benefit is ln(-1) = ln(1 eiπ ) = πi. (And you thought you couldn't handle negative logarithms!) You can, but the results aren't accurate.)
Other base logarithms (including ) can be found using the change-of-base formula.
Log4 e = ln e/ ln i = 1/ πi/2 = -2i/π
Complex bases). For example,
Q12) Explain Cauchy-Riemann Equations.
A12)
Let
f(x, y) ≡ u(x, y) + iv(x, y)
Where
z ≡ x+ iy
So
Dz = dx + i dy
After that, the total derivative of with respect to is
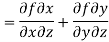
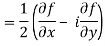
In the context of and, (5) becomes
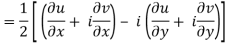
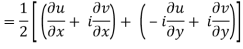
Along the x-axis, or real axis,
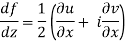
Along the y-axis, or imaginary axis,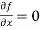 , so
, so
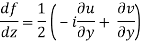
If f is complex differentiable, then the value of the derivative must be the same for a given dz, Regardless of how it is oriented As a result, (8) must equal (9), implying that
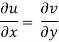
And
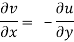
The Cauchy-Riemann equations are what they're called.
They are the causes of the disorders.
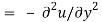
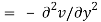
Where 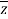 is the complex conjugate.
is the complex conjugate.
If z = r eiθ, then the Cauchy-Riemann equations become
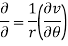
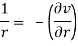
(Abramowitz and Stegun 1972, p. 17).
In two dimensions, if and satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation.
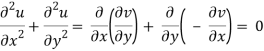
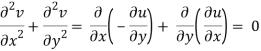
Solutions that fulfil the Cauchy-Riemann equations and Laplace's equation can be found by picking an arbitrary. This fact is utilised to solve physical problems involving scalar potentials, such as fluid flow and electrostatics, using conformal mappings.
Q13) Explain Linear Fractional Transformations.
A13)
The linear fractional transformations or Mobius transformations, the rational functions of degree one, are of central importance among the rational functions:
w = T(z) = 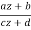 ,(8)
,(8)
Where ad bc 6=0 and a, b, c, and d are complex numbers. We may show that any linear fractional transformation T has an inverse by solving for z as a function of w.
z = T-1(w) =  ,
,
As though checking with a calculator As a result, linear fractional transformations are always one-to-one and represented as C-to-C maps. Indeed, they are the only complex analytic functions from C to themselves that have complex analytic inverses.
Furthermore, the composition of two linear fractional transformations is simply verified to be another linear fractional transformation. Composition transforms the space of linear fractional transformations into a group, as algebraists term it.
The linear fractional transformation becomes a complex linear transformation when c = 0 and d = 1.
z 7→w = T(z) = az + b.
The following are examples of sophisticated linear transformations:
Translationsz 7→w = T(z) = z + b,
Rotationsz →7 w = T(z) = eiθz,
And expansions and contractionsz →7 w = T(z) = ρz,
Where and are real numbers, both of which are nonzero. When a = d = 0 and b = c = 1, the linear fractional transformation reduces to an inversion
w = T(z) = 1/z
T is a reflection in the circle in this case.
z ↦ 1/z reiθ ↦ 1/r eiθ
Q14) Describe Dangerous curve.
A14)
A multiple-valued function is not the same as a true function as studied in the rest of mathematics. For a given argument choice, a valid function can only assume one value. Nonetheless, the concept of a multiple-valued function is widely utilised in complex variable theory since it is extremely valuable. In more advanced complex variable treatments, multiple-valued functions on open subsets of the complex plane are replaced with true single-valued functions defined on "Riemann surfaces" over the open subsets (see [2]).
We may erase the uncertainty in the logarithm by replacing it, as we saw earlier.
C−{0} by the smaller domain
D = C−{x + iy ∈C : x ≤ 0},(15)
And choosing a branch of the muliple-valued function log that is single-valued in D. We do this by first letting Arg(w) be the value of the angular coordinate θ which lies in the interval (−π,π] and then define
Log : D −→C byLog(w) = Log(|w|) = iArg(w).
Choosing a branch does give us a genuine single-valued complex analytic logarithm function, and as we saw when discussing the Cauchy-Riemann equations,
d/dw Log (w) = 1/w
However, this destroys some of the nice properties one might hope for the logarithm; for example, although
Log(z1z2) = log(z1) + log(z2),
Where equality means that the values taken by the multiple-valued functions on the two sides are the same, it is not true that
Log(z1z2) = Log(z1) + Log(z2)
In general.
One of the most useful applications of the multiple-valued logarithm function is in defining arbitrary powers of a complex number. The definition is motivated by the fact that zn = exp(nlog(z)), when n ∈N.
Q15) What is Singular Function?
A15)
A singularity is a point when an equation, surface, or other object blows up or degenerates. Singularities are also referred to as singular points.
Singularities play a crucial role in complex analysis, as they define the range of conceivable behaviours for analytic functions. Complex singularities are spots in a function's domain where the function fails to be analytic. Poles, essential singularities, logarithmic singularities, and detachable singularities are all types of isolated singularities. Natural boundaries or branch cuttings can produce nonisolated singularities.
Consider the ordinary differential equation of second order.
y’’ + P(x) y’ + Q(x)y = 0 |
If and stay finite at, then is referred to be an ordinary point. When either or diverges as, the result is referred to as a unique point. Singular points are further divided into the following categories:
1. If either or diverges as but remains finite as, is referred to as a normal singular point (or nonessential singularity).
2. If diverges faster than and approaches infinity as, or diverges faster than and goes to infinity as, then is referred to as an irregular singularity (or essential singularity).
A point of such that the Laurent series of has for and is referred to as a pole of order.
Essential singularities are infinite-order poles. A pole of order is a singularity of for which the function is nonsingular but is singular for, 1,...,.
A logarithmic singularity is an analytic function singularity with a primary -dependent term of order,, etc.
Singularities that may be assigned a complex number in such a way that it becomes analytic are known as removable singularities. For example, the function has a detachable singularity at 0 since it is equal to 0 everywhere except 0. Singularities that can be removed are not poles.
The function, for example, exhibits two singularities: poles at and a nonisolated singularity at 0.
Q16) What is Branch cuts? in Singular Function.
A16)
A branch cut is a curve in the complex plane in which an analytic multivalued function is discontinuous (having ends that may be open, closed, or half-open). Branch cuts are frequently represented as lines or line segments for ease of use. Cut lines (Arfken 1985, p. 397), slits (Kahan 1987), and branch lines are all terms used to describe branch cuts (including ones with curves).
Take, for example, the function that converts each complex number to a well-defined number. Its inverse function, on the other hand, transfers the value to, for example. While such functions can have a single primary value (in this case, the main square root is positive), the choices cannot be made continuously across the complex plane. Instead, discontinuity lines must be drawn. The implementation of so-called branch cuts is the most prevalent method for coping with these discontinuities. Branch cuts are not unique in general; instead, they are chosen by convention to provide easy analytic features (Kahan 1987). Some functions have a relatively simple branch cut structure, while others have exceedingly intricate branch cuts.
Riemann surfaces are a multivalued function representation alternative to branch cuts.
Singularities known as branch points exist in addition to branch cuts. It should be emphasised, however, that branch cut endpoints are not always branch points.
The single-valued trigonometric, hyperbolic, integer power, and exponential functions do not have branch cuts. Their multivalued inverses, on the other hand, necessitate branch cuts. The graphs and table below show the branch cut structure of the Wolfram Language's inverse trigonometric, inverse hyperbolic, noninteger power, and logarithmic functions.
Q17) Explain Cauchy’s Inequality.
A17)
A special case of Hölder's sum inequality with p = q= 2,
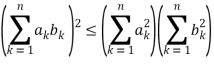
In two-dimensions, it becomes
(a2 + b2)(c2 + d2) ≥ (ac + bd)2
It can be proven by writing
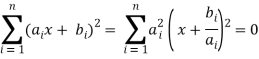
If 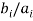 is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
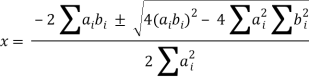
In order for this to be complex, it must be true that
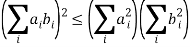
With equality when bi/ai is a constant. The vector derivation is much simpler,
(a . b)2 = a2 b2 cos2 θ ≤ a2 b2
Where
a2 = a . a = 
And similarly for b.
Q18) Explain Cauchy’s integral formula.
A18)
Cauchy's integral formula, named after Augustin-Louis Cauchy, is a key statement in complex analysis in mathematics. It reflects the fact that the values on the disk's boundary entirely determine a holomorphic function defined on the disc, and it gives integral formulas for all derivatives of a holomorphic function. Cauchy's formula demonstrates that "differentiation is comparable to integration" in complex analysis: complex differentiation, like integration, performs well within uniform boundaries, a result that does not hold in real analysis.
Assume that U is an open subset of the complex plane C, and that D is a closed disc.
D = { z : |z – z0| ≤ r}
Is entirely confined within U. Let f : U C be a holomorphic function, and let be the counterclockwise-oriented circle that forms D's boundary. Then, for each an in D's interior,
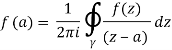
This statement is proved using the Cauchy integral theorem, which, like that theorem, just needs that f is complex differentiable. Since 1/(z-a) can be expanded as a power series in the variable 𝑎:

— it follows that holomorphic functions are analytic, i.e. they can be expanded as convergent power series. In particular f is actually infinitely differentiable, with
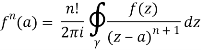
Cauchy's differentiation formula is another name for this formula.
Q19) Write the Definition of Simply Connected.
A19)
A simply connected domain is a path-connected domain in which every simple closed curve can be constantly shrunk into a point while remaining in the domain.

For two-dimensional regions, a simply connected domain is one without holes in it.
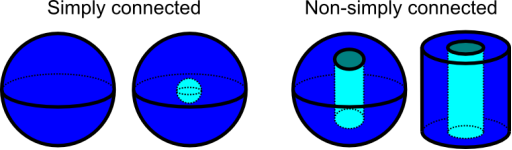
The concept of simply connected is more subtle in three-dimensional spaces. A domain that is simply connected has no gaps running through it. However, a domain with just a hole in the middle (like a ball whose center is hollow) is still simply connected, as we can continuously shrink any closed curve to a point by going around the hole and remaining in the domain. A ball with a hole bored all the way through it, or a spool with a hollow centre axis, on the other hand, cannot be simply linked. While remaining in the domain, a closed curve that travelled around the hole could not be shortened to a point. Because there is no way for the curve to avoid the hole, it is locked around it.
Q20) Explain Laurent Series.
A20)
If is analytic in the annular area between and on the concentric circles, and is centred at and of radii, then there exists a unique series expansion in terms of positive and negative powers of.
(z-a),
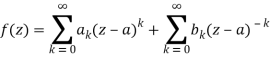
Where

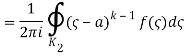
(Korn and Korn 1968, pp. 197-198).
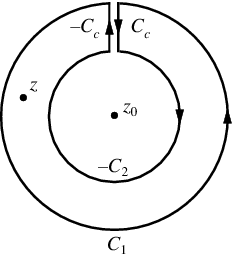
Let's say there are two circular shapes and, one having a radius that is larger than that of the other. Allow to be at the intersection of and, and between and. Create a cut line between and and integrate it around the path so that the plus and minus contributions cancel each other out, as shown above. The integral formula of Cauchy is as follows:

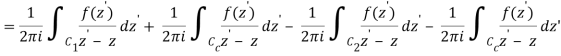
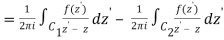
Now, because the cut line's contributions in opposite directions cancel each other out,
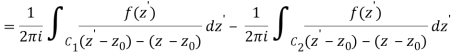
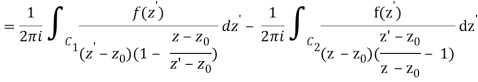
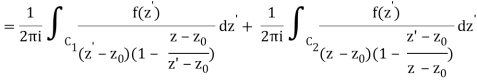
Q21) Explain Taylor Series for Real Functions.
A21)
Let a∈R and f(x) be and infinitely differentiable function on an interval I containing a. The Taylor series of f around an in one dimension is thus given by
f(x) = f(a) + f’ (a) (x – a) + f’’(a)/2! (x –a)2 + f(3)(a)/3! (x – a)3 + ...
Which can be written in the most compact form:
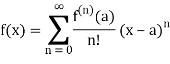 Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
The best linear approximation for f(x) is, for example,
f(x) ≈ f(a) + f’(a) (x – a)
This linear approximation matches the slope of f at a by fitting f(x) with a line through x=a.
We can improve the approximation by including more terms in the expansion. The best quadratic approximation, for example, is
f(x) ≈ f(a) + f’(a)(x – a) + ½ f’’ (a) (x – a)2
The partial sums of the Taylor series for a given function are displayed in the applet below. To see more terms from the series, move the slider. Change the function or drag the point a.
Unit - 1
Complex Analysis
Q1) Define Complex, Real and Imaginary number in mathematics.
A1)
Complex number
A complex number is a number that is made up of both real and imaginary numbers. The complex number is in the form of a+ib, where a = real number and ib = imaginary number. In addition, a,b are real values, and I = -1.
Hence, a complex number is a simple representation of addition of two numbers, i.e., real number and an imaginary number. One side is entirely genuine, while the other is entirely imagined.
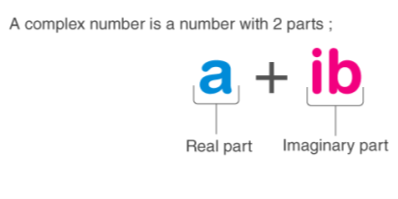
Real Numbers
Real numbers are any numbers that exist in a number system, such as positive, negative, zero, integer, rational, irrational, fractions, and so on. Re is the symbol for it (). 12, -45, 0, 1/7, 2.8, 5, and other real numbers are examples.
Imaginary Numbers
Imaginary numbers are numbers that are not real. We get a negative return when we square an imaginary number. Im is the symbol for it (). For example, the numbers -2, -7, and 11 are all fictional.
To answer the equation x2+1 = 0, complex numbers were introduced. The equation's roots are of the form x = -1, and there are no true roots. As a result of the addition of complex numbers, we now have imaginary roots.
The symbol I which stands for Iota, is used to represent -1. (Imaginary number).
Q2) What is Representation of Z modulus on Argand Plane?
A2)
Argand plane consists of real axis (x – axis) and imaginary axis (y – axis).
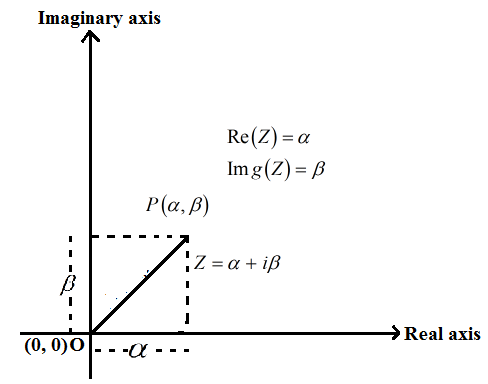
|Z| = √(α – 0)2 + (β – 0)2
= √(α )2 + (β)2
= √Re (z )2 + Img (z)2
|z| = | α + iβ| = √(α )2 + (β)2
Q3) What is Conjugate of Complex Numbers on argand plane?
A3)
A complex number's conjugate is a number with the same real portion and the opposite sign of the imaginary portion but identical magnitude.
The complex number Z = + I will be used.
The conjugate of a particular complex number will be represented as the mirror image of Z = + I along the real axis.
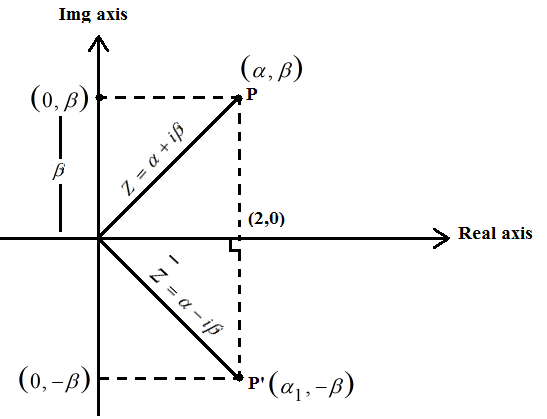
Z = α + iβ (complex number)
 (conjugate of complex number)
(conjugate of complex number)
Q4) Explain Distance Between Two Points in Complex Plane.
A4)
In the argand plane, if two complex integers Z1 and Z2 are labelled as P and Q, respectively, the distance between P and Q is given as.
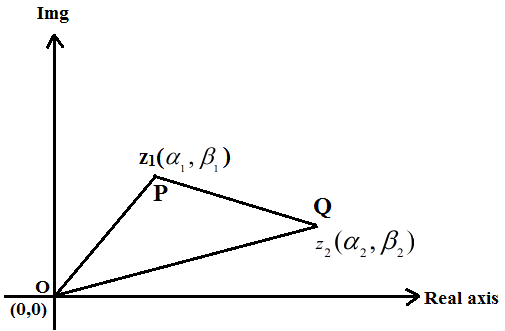
PQ = |z2 – z1| = |(α2 – α1) + i(β2 – β1)| = √( α2 – α1)2 + (β2 – β1)2
For example, Find the distance of a point P, Z = (3 + 4i) from origin.
Solution:

|Z| = |3 + 4i|
= √ 32 + 42 = 5 units
Q5) Write a Short note on Polar form of Complex number.
A5)
Both rectangular and polar coordinates can be used to represent complex values. We'll look at the polar form of any complex number here.
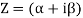
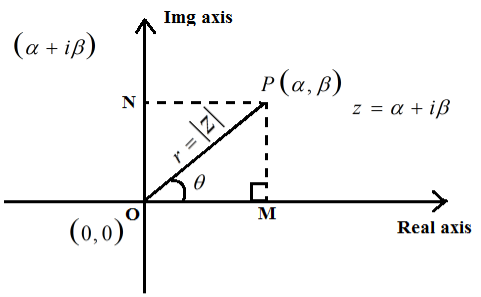
Z = α + iβ, |z| = r
OM = r cos θ = α
ON = r sin θ = β
Hence, Z = α + iβ
= (OM) + i (ON)
= r cos θ + i r sin θ = r( cos θ + i sin θ) r = 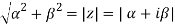
Where ‘' stands for complex number argument.
θ = arg (z)
For a complex number's conjugate
Arg (
Q6) Explain Product of two Complex number.
A6)
Let P and Q represent complex number
Z1=(α1+iβ1) and
Z2=(α2+iβ2) in argand plane
θ1=arg(z1),
θ2=arg(z2) (given)
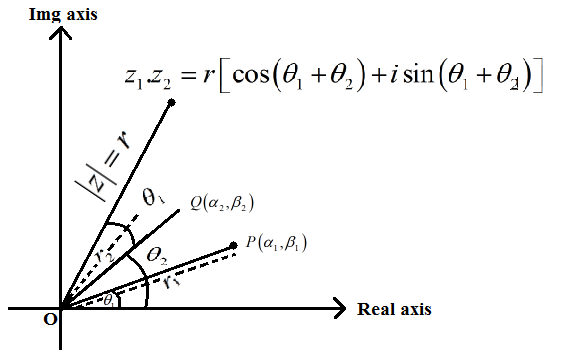
Now, on multiplying Z1 Z2 = Z
Z = ( α1 + i β1) ( α2 + i β2) = r1 ( cos θ1 + i sin θ1). r2 ( cos θ2 + i sin θ2)=
r1r2[ cos(θ1 + θ2) + i sin (θ1 + θ2)]
Let say r1. r2 = r
Z = r( cos(θ1 + θ2) + i sin (θ1 + θ2))
Q7) Explain Derivation 1: Power Series in Details.
A7)
The use of power series is one of the more intuitive derivations of Euler's formula. It entails expanding the exponential, sine, and cosine power series to arrive at the conclusion that the equivalence holds.
As a precaution, this method presupposes that the sinz, cosz, and ez power series expansions are perfectly convergent everywhere (e.g., that they hold for all complex numbers z). It does, however, have the advantage of demonstrating that Euler's formula holds for all complex numbers z.
The power series expansion of ez for a complex variable z is
ez = 1 + z/ 1! + z2/2! + z3/3! + z4/4! + . . .
Let's pretend that z is ix (where x is an arbitrary complex number). I am raised to greater powers as z is raised to greater abilities. The first eight powers of I are as follows:
i0 = 1 i4 = i2 . i2 = 1
i1 = i i5 = i . i4 =i
i2 = 1 (by the definition of i) i6 = i . i5 = -1
i3 = i . i2 = - i i7 = i . i6 = -i
(Notice how the powers of I are cyclical: 1, I 1, i. We'll be putting these abilities to good use soon.)
When z=ix, the expansion of ez is as follows:
eix = 1 + ix + (ix)2/2! + (ix)3/3! + (ix)4/4! + . . .
We get the following results when we extract the powers of I
eix = 1 + ix - (ix)2/2! - (ix)3/3! + (ix)4/4! + (ix)5/5! - (ix)6/6! - (ix)7/7! + (ix)8/8! +. . .
We can rearrange the terms of ez's power series expansion without changing its value because it is totally convergent. The result of combining the real and imaginary terms is
eix = (1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .) + i (x – x3/3! + x5/5! – x7/7! +. . .)
Let's take a detour and look at the sine and cosine power series. The cos x power series is
Cos x = 1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .
And for sinx, it is
Sin x = x – x3/3! + x5/5! – x7/7! +. . .
To put it another way, the last equation we had was exact.
eix = cos x + i sin x
This is the Euler's formula statement we were seeking for.
Q8) Give the Applications Of Complex Numbers.
A8)
Euler's formula, as one of the most important equations in mathematics, has a plethora of interesting applications in a variety of fields. These include, for example:
- The famous Euler's identity The exponential form of complex numbers Trigonometric and hyperbolic functions with different meanings
- Exponential and logarithmic functions are generalised to complex numbers.
- De Moivre's theorem alternate proofs and trigonometric additive identities
- Euler's Personality
- Euler's identity is frequently regarded as mathematics' most beautiful equation. It's written like this:
- Ei+1=0 ei+1=0 ei+1=0 ei
- Where five of the most essential constants in mathematics are highlighted. These are the following:
- The identity of addition 0
- The unity number one
- The Pi constant (circumference to diameter ratio) is a mathematical constant.
- e is the natural logarithm's base.
- The fictitious unit I
Q9) What is De Moivre’s theorem?
A9)
De Moivre's theorem establishes a formula for computing complex number powers. Consider what occurs when we multiply a complex number by itself to obtain some idea for de Moivre's theorem.
Remember that any complex number z=a+ib can be expressed as with the polar form.
Then squaring the complex number z gives
z2 =(r( cos θ + i sin θ))2
= r2( cos θ + i sin θ)2
= r2( cos θ cos θ + i sin θ cos θ + i sin θ cos θ + i2 sin θ sin θ)
= r2((cos θ cos θ – sin θ sin θ) + i(sin θ cos θ + sin θ cos θ))
= r2(cos 2 θ + i sin 2 θ)
This demonstrates that squaring a complex integer squares the absolute value and multiplies the argument by two. For n3, de Moivre's theorem shows that to increase a complex number to the nth power, the absolute value must be raised to the nth power, and the argument must be multiplied by n.
Q10) Write a Short note Roots of Complex Numbers.
A10)
Let z be a complex number that is not zero. Then in C, there are exactly k many kth roots of z.
Assume that w is a complex number. We want to identify all z such that zn=w, or the nth roots of w.
There are n different nth roots, which can be discovered in the following order:.
- Write z and w in polar form as z=rei,w=sei. Zn=w then becomes:
(reiθ)n = rneinθ = seiϕ
We need to solve for r and θ.
2. Solve the following two equations:
rn=s
einθ=eiϕ
3. The solutions to rn=s are given by r= .
.
4. The solutions to einθ=eiϕ are given by
nθ = ϕ + 2 πl, for l = 0, 1, 2, . . ., n - 1
Or
θ = ϕ/n + 2/n πl, for l = 0, 1, 2, . . . , n -1
5. Using the solutions r,θ to the equations given in construct the nth roots of the form z=reiθ.
Q11) What is Logarithm functions?
A11)
Because a complex number can be expressed as an exponential function, reiP , A logarithm is nearly instantaneous. We get it. Ln reiP = ln r + ln eiP = ln r + iP , This is the natural logarithm's primary value. The angle PP, on the other hand, is not unique, as it can vary by multiples of two. As a result, the formula for a complex number's natural logarithm is ln reiP = ln r + iP + 2kπi
We can find the natural logarithm of I for example. Its main benefit is
Ln i = ln (1 eiπ/2) = π/2 i
The natural logarithm of negative one is another fascinating example. Its main benefit is ln(-1) = ln(1 eiπ ) = πi. (And you thought you couldn't handle negative logarithms!) You can, but the results aren't accurate.)
Other base logarithms (including ) can be found using the change-of-base formula.
Log4 e = ln e/ ln i = 1/ πi/2 = -2i/π
Complex bases). For example,
Q12) Explain Cauchy-Riemann Equations.
A12)
Let
f(x, y) ≡ u(x, y) + iv(x, y)
Where
z ≡ x+ iy
So
Dz = dx + i dy
After that, the total derivative of with respect to is
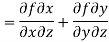
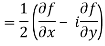
In the context of and, (5) becomes
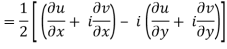
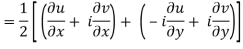
Along the x-axis, or real axis,
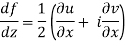
Along the y-axis, or imaginary axis, , so
, so
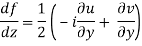
If f is complex differentiable, then the value of the derivative must be the same for a given dz, Regardless of how it is oriented As a result, (8) must equal (9), implying that
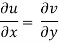
And
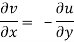
The Cauchy-Riemann equations are what they're called.
They are the causes of the disorders.
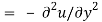
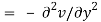
Where 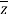 is the complex conjugate.
is the complex conjugate.
If z = r eiθ, then the Cauchy-Riemann equations become
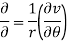
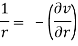
(Abramowitz and Stegun 1972, p. 17).
In two dimensions, if and satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation.
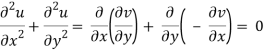

Solutions that fulfil the Cauchy-Riemann equations and Laplace's equation can be found by picking an arbitrary. This fact is utilised to solve physical problems involving scalar potentials, such as fluid flow and electrostatics, using conformal mappings.
Q13) Explain Linear Fractional Transformations.
A13)
The linear fractional transformations or Mobius transformations, the rational functions of degree one, are of central importance among the rational functions:
w = T(z) = 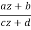 ,(8)
,(8)
Where ad bc 6=0 and a, b, c, and d are complex numbers. We may show that any linear fractional transformation T has an inverse by solving for z as a function of w.
z = T-1(w) =  ,
,
As though checking with a calculator As a result, linear fractional transformations are always one-to-one and represented as C-to-C maps. Indeed, they are the only complex analytic functions from C to themselves that have complex analytic inverses.
Furthermore, the composition of two linear fractional transformations is simply verified to be another linear fractional transformation. Composition transforms the space of linear fractional transformations into a group, as algebraists term it.
The linear fractional transformation becomes a complex linear transformation when c = 0 and d = 1.
z 7→w = T(z) = az + b.
The following are examples of sophisticated linear transformations:
Translationsz 7→w = T(z) = z + b,
Rotationsz →7 w = T(z) = eiθz,
And expansions and contractionsz →7 w = T(z) = ρz,
Where and are real numbers, both of which are nonzero. When a = d = 0 and b = c = 1, the linear fractional transformation reduces to an inversion
w = T(z) = 1/z
T is a reflection in the circle in this case.
z ↦ 1/z reiθ ↦ 1/r eiθ
Q14) Describe Dangerous curve.
A14)
A multiple-valued function is not the same as a true function as studied in the rest of mathematics. For a given argument choice, a valid function can only assume one value. Nonetheless, the concept of a multiple-valued function is widely utilised in complex variable theory since it is extremely valuable. In more advanced complex variable treatments, multiple-valued functions on open subsets of the complex plane are replaced with true single-valued functions defined on "Riemann surfaces" over the open subsets (see [2]).
We may erase the uncertainty in the logarithm by replacing it, as we saw earlier.
C−{0} by the smaller domain
D = C−{x + iy ∈C : x ≤ 0},(15)
And choosing a branch of the muliple-valued function log that is single-valued in D. We do this by first letting Arg(w) be the value of the angular coordinate θ which lies in the interval (−π,π] and then define
Log : D −→C byLog(w) = Log(|w|) = iArg(w).
Choosing a branch does give us a genuine single-valued complex analytic logarithm function, and as we saw when discussing the Cauchy-Riemann equations,
d/dw Log (w) = 1/w
However, this destroys some of the nice properties one might hope for the logarithm; for example, although
Log(z1z2) = log(z1) + log(z2),
Where equality means that the values taken by the multiple-valued functions on the two sides are the same, it is not true that
Log(z1z2) = Log(z1) + Log(z2)
In general.
One of the most useful applications of the multiple-valued logarithm function is in defining arbitrary powers of a complex number. The definition is motivated by the fact that zn = exp(nlog(z)), when n ∈N.
Q15) What is Singular Function?
A15)
A singularity is a point when an equation, surface, or other object blows up or degenerates. Singularities are also referred to as singular points.
Singularities play a crucial role in complex analysis, as they define the range of conceivable behaviours for analytic functions. Complex singularities are spots in a function's domain where the function fails to be analytic. Poles, essential singularities, logarithmic singularities, and detachable singularities are all types of isolated singularities. Natural boundaries or branch cuttings can produce nonisolated singularities.
Consider the ordinary differential equation of second order.
y’’ + P(x) y’ + Q(x)y = 0 |
If and stay finite at, then is referred to be an ordinary point. When either or diverges as, the result is referred to as a unique point. Singular points are further divided into the following categories:
1. If either or diverges as but remains finite as, is referred to as a normal singular point (or nonessential singularity).
2. If diverges faster than and approaches infinity as, or diverges faster than and goes to infinity as, then is referred to as an irregular singularity (or essential singularity).
A point of such that the Laurent series of has for and is referred to as a pole of order.
Essential singularities are infinite-order poles. A pole of order is a singularity of for which the function is nonsingular but is singular for, 1,...,.
A logarithmic singularity is an analytic function singularity with a primary -dependent term of order,, etc.
Singularities that may be assigned a complex number in such a way that it becomes analytic are known as removable singularities. For example, the function has a detachable singularity at 0 since it is equal to 0 everywhere except 0. Singularities that can be removed are not poles.
The function, for example, exhibits two singularities: poles at and a nonisolated singularity at 0.
Q16) What is Branch cuts? in Singular Function.
A16)
A branch cut is a curve in the complex plane in which an analytic multivalued function is discontinuous (having ends that may be open, closed, or half-open). Branch cuts are frequently represented as lines or line segments for ease of use. Cut lines (Arfken 1985, p. 397), slits (Kahan 1987), and branch lines are all terms used to describe branch cuts (including ones with curves).
Take, for example, the function that converts each complex number to a well-defined number. Its inverse function, on the other hand, transfers the value to, for example. While such functions can have a single primary value (in this case, the main square root is positive), the choices cannot be made continuously across the complex plane. Instead, discontinuity lines must be drawn. The implementation of so-called branch cuts is the most prevalent method for coping with these discontinuities. Branch cuts are not unique in general; instead, they are chosen by convention to provide easy analytic features (Kahan 1987). Some functions have a relatively simple branch cut structure, while others have exceedingly intricate branch cuts.
Riemann surfaces are a multivalued function representation alternative to branch cuts.
Singularities known as branch points exist in addition to branch cuts. It should be emphasised, however, that branch cut endpoints are not always branch points.
The single-valued trigonometric, hyperbolic, integer power, and exponential functions do not have branch cuts. Their multivalued inverses, on the other hand, necessitate branch cuts. The graphs and table below show the branch cut structure of the Wolfram Language's inverse trigonometric, inverse hyperbolic, noninteger power, and logarithmic functions.
Q17) Explain Cauchy’s Inequality.
A17)
A special case of Hölder's sum inequality with p = q= 2,
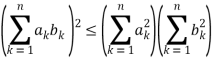
In two-dimensions, it becomes
(a2 + b2)(c2 + d2) ≥ (ac + bd)2
It can be proven by writing
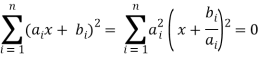
If 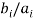 is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
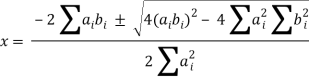
In order for this to be complex, it must be true that
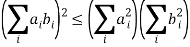
With equality when bi/ai is a constant. The vector derivation is much simpler,
(a . b)2 = a2 b2 cos2 θ ≤ a2 b2
Where
a2 = a . a = 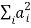
And similarly for b.
Q18) Explain Cauchy’s integral formula.
A18)
Cauchy's integral formula, named after Augustin-Louis Cauchy, is a key statement in complex analysis in mathematics. It reflects the fact that the values on the disk's boundary entirely determine a holomorphic function defined on the disc, and it gives integral formulas for all derivatives of a holomorphic function. Cauchy's formula demonstrates that "differentiation is comparable to integration" in complex analysis: complex differentiation, like integration, performs well within uniform boundaries, a result that does not hold in real analysis.
Assume that U is an open subset of the complex plane C, and that D is a closed disc.
D = { z : |z – z0| ≤ r}
Is entirely confined within U. Let f : U C be a holomorphic function, and let be the counterclockwise-oriented circle that forms D's boundary. Then, for each an in D's interior,
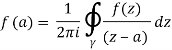
This statement is proved using the Cauchy integral theorem, which, like that theorem, just needs that f is complex differentiable. Since 1/(z-a) can be expanded as a power series in the variable 𝑎:
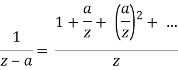
— it follows that holomorphic functions are analytic, i.e. they can be expanded as convergent power series. In particular f is actually infinitely differentiable, with
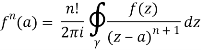
Cauchy's differentiation formula is another name for this formula.
Q19) Write the Definition of Simply Connected.
A19)
A simply connected domain is a path-connected domain in which every simple closed curve can be constantly shrunk into a point while remaining in the domain.

For two-dimensional regions, a simply connected domain is one without holes in it.
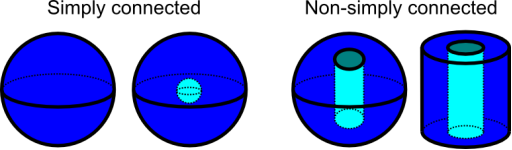
The concept of simply connected is more subtle in three-dimensional spaces. A domain that is simply connected has no gaps running through it. However, a domain with just a hole in the middle (like a ball whose center is hollow) is still simply connected, as we can continuously shrink any closed curve to a point by going around the hole and remaining in the domain. A ball with a hole bored all the way through it, or a spool with a hollow centre axis, on the other hand, cannot be simply linked. While remaining in the domain, a closed curve that travelled around the hole could not be shortened to a point. Because there is no way for the curve to avoid the hole, it is locked around it.
Q20) Explain Laurent Series.
A20)
If is analytic in the annular area between and on the concentric circles, and is centred at and of radii, then there exists a unique series expansion in terms of positive and negative powers of.
(z-a),
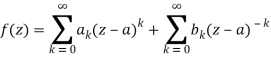
Where

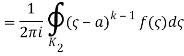
(Korn and Korn 1968, pp. 197-198).
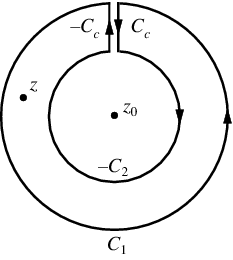
Let's say there are two circular shapes and, one having a radius that is larger than that of the other. Allow to be at the intersection of and, and between and. Create a cut line between and and integrate it around the path so that the plus and minus contributions cancel each other out, as shown above. The integral formula of Cauchy is as follows:
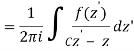
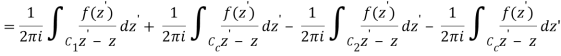

Now, because the cut line's contributions in opposite directions cancel each other out,
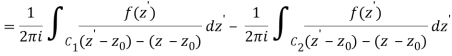
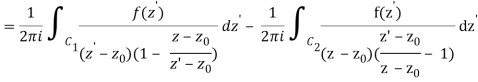
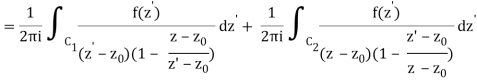
Q21) Explain Taylor Series for Real Functions.
A21)
Let a∈R and f(x) be and infinitely differentiable function on an interval I containing a. The Taylor series of f around an in one dimension is thus given by
f(x) = f(a) + f’ (a) (x – a) + f’’(a)/2! (x –a)2 + f(3)(a)/3! (x – a)3 + ...
Which can be written in the most compact form:
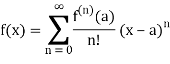 Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
The best linear approximation for f(x) is, for example,
f(x) ≈ f(a) + f’(a) (x – a)
This linear approximation matches the slope of f at a by fitting f(x) with a line through x=a.
We can improve the approximation by including more terms in the expansion. The best quadratic approximation, for example, is
f(x) ≈ f(a) + f’(a)(x – a) + ½ f’’ (a) (x – a)2
The partial sums of the Taylor series for a given function are displayed in the applet below. To see more terms from the series, move the slider. Change the function or drag the point a.