Unit - 3
Integral Transforms-II
Q1) What is Convolution theorem?
A1)
Let f(t) and g(t) be arbitrary functions of time  with Fourier transforms. Take
with Fourier transforms. Take
f(t) = F-1v [F(v)](t) = 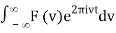
g(t) = F-1v [G(v)](t) = 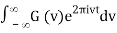
Where F-1v (t) denotes the inverse Fourier transform (where the transform pair is defined to have constants A = 1 and B = - 2π). Then the convolution is
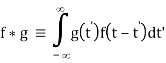
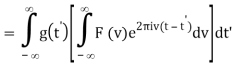
Interchange the order of integration,
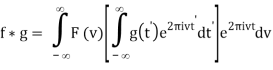
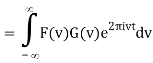
= Fv-1 [F(v) G(v)] (t)
So, applying a Fourier transform to each side, we have
F[f * g] = F[f] F[g]
The convolution theorem also takes the alternate forms
F[fg] = F[f] * F[g]
F-1 (F[f] F[g]) = f * g
F-1(F[f] * F[g]) = f g
Q2) Explain Properties of fourier transform.
A2)
The z-transform has features that are similar to those of the Fourier transform (and Laplace transform). The only distinction is that the ROCs require extra attention. Assumptions are made in the following sections.
Z [ x[n]] = X(z) ROC = Rx
And
Z [ y[n]] = Y(z) ROC = Ry
Linearity
Z [ ax[n] + by[n]] = a X(z) + bY(z), ROC ⊇ (Rx ∩ Ry)
While it is obvious that the ROC of the linear combination of x[n] and y[n] should be the intersection of the their individual ROCs Rx ∩ Ry in which both X(z) and Y(z) exist, note that in some cases the ROC of the linear combination could be larger than Rx ∩ Ry. For example, for both x[n] = anu[n] and y[n] = anu[n-1] , the ROC is |z| > |a| , but the ROC of their difference an u[n] – anu[n – 1] = δ[n] is the entire z-plane.
Time Shifting
Z[x[n – n0]] = Z-n0 X(z), ROC = Rx
Proof:
Z[x[n – n0]] = 
Define m = n – n0, we have n = m + n0 and
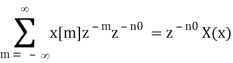
The new ROC is identical to the previous one, with the exception of the possibility of adding or removing the origin or infinity, as the shift may affect the signal's duration.
Q3) Give the Example of Time Expansion (Scaling).
A3)
Example: If x[n] is ramp
n | 1 | 2 | 3 | 4 | 5 | 6 |
x[n] | 1 | 2 | 3 | 4 | 5 | 6 |
Then the expanded version x[n/2] is
n | 1 | 2 | 3 | 4 | 5 | 6 |
n/2 | 0.5 | 1 | 1.5 | 2 | 2.5
| 3 |
m |
| 1 |
| 2 |
| 3 |
x[n/2] | 0
| 1
| 0 | 2 | 0 | 3 |
Where m is the integer part of n/k.
Proof: The z-transform of a signal like this is
Z[x[n/k]] = 
Note that the change of the summation index from n to m has no effect as the terms skipped are all zeros.
Q4) Explain Time Difference with Proof.
A4)
Z[x[n] – x[n – 1]] = (1 – z-1)X(z), ROC = Rx
Proof:
Z[x[n] – x[n – 1]] = X(z) – z-1 X(z) = (1 – z-1) X(z) = z – 1/z X(z)
Note that due to the additional zero z = 1 and pole z = 0, the resulting ROC is the same as Rx except the possible deletion of z = 0 caused by the added pole and/or addition of z = 1 caused by the added zero which may cancel an existing pole.
Q5) Explain Time Accumulation with Proof.
A5)
Z[  =
= 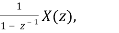 ROC ⊇ [Rx ∩ (|z| > 1)]
ROC ⊇ [Rx ∩ (|z| > 1)]
Proof: The accumulation of x[n] can be written as its convolution with u[n]:
u[n] * x[n] = 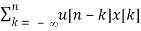 =
= 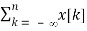
Applying the convolution property, we get
Z[ 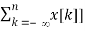 = Z[u[n] * x[n]] =
= Z[u[n] * x[n]] = 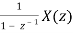
As Z[u[n]] = 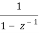
Q6) Explain Scaling in Z-domain with Proof.
A6)
Z[an x[n]] = X(z/a), ROC = |a| Rx
Proof:
Z[an x[n]] = 
In particular, if a = ej0 , the above becomes
Z[ejn0 x[n]] = X(e-j0 z) ROC = Rx
The multiplication by e-j0 to z corresponds to a rotation by angle 0 in the z-plane, i.e., a frequency shift by 0. The rotation is either clockwise (0 > 0) or counter clockwise (0 < 0) corresponding to, respectively, either a left-shift or a right shift in frequency domain. The property is essentially the same as the frequency shifting property of discrete Fourier transform.
Q7) Explain the Example of Z-domain.
A7)
Z[nx[n]] = -z d/dz X(z), ROC = Rx
Proof:
d/dz X(z) = 
i.e.,
Z[nx[n]] = - z d/dz X(z)
Example: Taking derivative with respect to z of the right side of
Z[an u[n]] = 
We get

We have this feature of differentiation in the z-domain because of the property of differentiation in the z-domain.
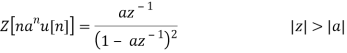
Note that for a different ROC |z| < |a|, we have
Z[ - nanu [ -n – 1]] = 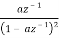 |z| < |a|
|z| < |a|
Q8) What is 3D Fourier Transform?
A8)
The Fourier pairs are naturally extended to three-dimensional functions as well.
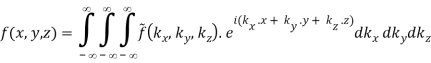
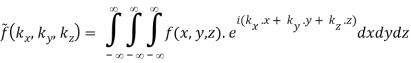
(B.39)
The 3D Fourier transform in cylindrical and spherical coordinates is then discussed.
Q9) Write a Short note on Cylindrical Coordinates.
A9)
In this case,
f(x, y, z) = g(r, θ,z)

(B.40)
Where,
x + iy = r . eiθ
kx + iky = 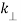 . eiθ
. eiθ
(B.41)
The functions g and 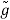 are related by
are related by

(B.42a)
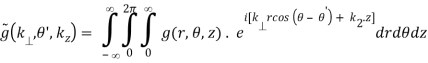
(B.42b)
Under circular symmetry, i.e., f independent of θ, and 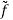 , thus, independent of
, thus, independent of 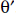 , we have
, we have
f(x, y, z) = h(r, z)
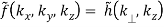
(B.43)
As a result, Eq. (B.42a-b) is formed (using the properties of the Hankel transform)
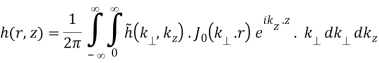
(B.44a)

(B.44b)
The integral in Eq. (B.44a) can be seen to represent a 1D Fourier transform of the Hankel transform with respect to r along z.
We have cylindrical symmetry if the problem has it, which means that f is independent of both and z.
f(x, y, z) = p(r)
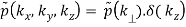
(B.45)
The Fourier transform can be reduced to
p(r) = 1/2π 
 (
(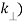 = 2π
= 2π 
(B.46)
Q10) Write a Short note on Spherical Coordinates.
A10)
In spherical coordinates,
f(x, y, z) = g(r, θ, )
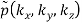 =
= 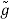 (k, θ’, ’)
(k, θ’, ’)
(B.47)
The coordinates are changed in the following way:
x = r sin θ cos , y = r sin θ sin , z = r cos θ
kx = k sin θ’ cos ’, ky = k sin θ’ sin ’, kz = k cos θ’
(B.48)
Where, again, k = 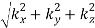 .
.
The Fourier integrals are transformed into
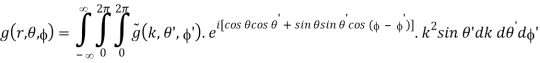

(B.49)
Under circular symmetry, i.e., f(x, y, z) is independent of , we have
f(x, y, z) = g(r, θ)

(B.50)
For circular symmetry, the Fourier transforms are

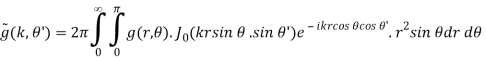
(B.51)
The function is independent of both angles for spherical symmetry, so we have
f(x, y, z) = h(r)
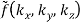 =
= 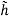 (k)
(k)
(B.52)
The integrals are reduced to in this case.

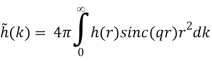
(B.53)
Q11) Write the Application of Fourier transform to differential equation.
A11)
The solution of differential equations can also be done using Fourier Transforms. To demonstrate this concept, we'll go over an Ordinary Differential Equation (ODE) and see how the Fourier Transform can be used to solve a differential equation.
Take a look at the ODE in Equation [1]:
d2y(t)/dt2 – y(t) = - g(t) [Equation 1]
The function y(t) that satisfies Equation [1] is what we're looking for. Why not take the Fourier Transform of an equation? We can take the Fourier Transform of a function, so why not an equation? It turns out there's no reason why we shouldn't be able to. Because the Fourier Transform is a linear operation, the time domain produces an equation in which each term corresponds to a frequency domain term. Equation [2] is obtained by applying the Fourier Transform to Equation [1]:
F{d2y(t)/dt2 } – F{ y(t)} = F{- g(t)} [Equation 2]
F{d2y(t)/dt2 } – Y(f) = - G(f)
If you recall the Fourier Transform's differentiation property, we can see that derivatives in the time domain become simple multiplication in the frequency domain:
F{dy(t)/dt} = (2πif)Y(f)
F{d2y(t)/dt2} = (2πif)2 Y(f). . . [Equation 3]
F{dny(t)/dtn} = (2πif)n Y(f)
Hence, Equation [2] becomes:
(2πif)2 Y(f) – Y(f) = - G(f) [Equation 4]
For Y(f), equation [4] is a simple algebraic equation! This is a simple problem to solve. The following is an example of how Fourier Transforms can be used to solve differential equations: They can solve algebraic equations by converting differential equations.
For Y(f), equation [4] can be easily solved:
Y(f) = -G(f)/(2πif)2 – 1 = G(f)/ 1+ 4π2f2 [Equation 5]
Q12) Explain 1D Wave Equation.
A12)
Consider problem
utt = c2uxx, - < x < , (32)
u|t=0 = g(x), (33)
ut|t=0 = h(x). (34)
We arrive at by performing a partial Fourier transform with respect to x.



Then characteristic equation for ODE (3535) is α2 = - c2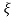 2 and α1,2 = ± ic
2 and α1,2 = ± ic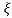
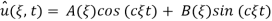
With initial conditions implying A(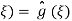 ,
,  and
and
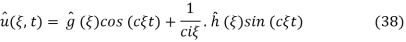
Rewriting 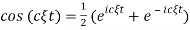 and recalling that multiplication of FT by
and recalling that multiplication of FT by  is equivalen to to shifting original to the left by b we conclude that
is equivalen to to shifting original to the left by b we conclude that 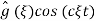 is a Fourier transform of ½ (g(x+ct) + g(x – ct))
is a Fourier transform of ½ (g(x+ct) + g(x – ct))
If we denote H as a primitive of hh then  which in virtue of the same arguments is FT of
which in virtue of the same arguments is FT of 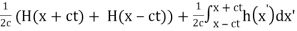
Therefore

We've returned to the d'Alembert formula.
Q13) What is Heat Equation?
A13)
Consider problem
ut = kuxx, t > 0, - < x < , (1)
u = g(x) (2)
= g(x) (2)
Making partial Fourier transform with respect to x↦ξ (so u(x,t)↦u^(ξ,t)) we arrive to


Indeed, ∂x↦iξ and therefore ∂2 x↦−ξ2
Note that (3) is an ODE and solving it we arrive to
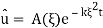 ; plugging into (4) we find that A(ξ) =
; plugging into (4) we find that A(ξ) = 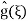 and therefore
and therefore
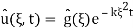
The right-hand expression is a product of two Fourier transforms, one is 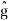 (ξ) and another is Fourier transform of IFT of e−kξ2te
(ξ) and another is Fourier transform of IFT of e−kξ2te
If we had 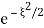 we would have IFT equal to
we would have IFT equal to 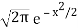 but we can get from
but we can get from 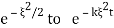 by scaling
by scaling 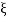 ↦ (2kt)-1/2
↦ (2kt)-1/2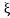 and therefore x ↦ (2kt)-1/2x (and we need to multiply the result by (2kt)-1/2 ; therefore
and therefore x ↦ (2kt)-1/2x (and we need to multiply the result by (2kt)-1/2 ; therefore 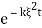 is a Fourier transform of
is a Fourier transform of 
Again:  is a product of FT of g and of
is a product of FT of g and of  and therefore uu is the convolution of these functions (multiplied by 1/(2π)):
and therefore uu is the convolution of these functions (multiplied by 1/(2π)):
u(x, t) = g * 1/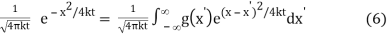
We recovered formula which we had already.
Unit - 3
Integral Transforms-II
Q1) What is Convolution theorem?
A1)
Let f(t) and g(t) be arbitrary functions of time  with Fourier transforms. Take
with Fourier transforms. Take
f(t) = F-1v [F(v)](t) = 
g(t) = F-1v [G(v)](t) = 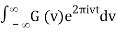
Where F-1v (t) denotes the inverse Fourier transform (where the transform pair is defined to have constants A = 1 and B = - 2π). Then the convolution is
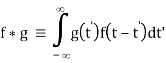
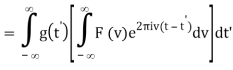
Interchange the order of integration,
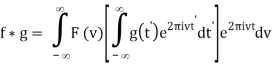
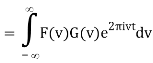
= Fv-1 [F(v) G(v)] (t)
So, applying a Fourier transform to each side, we have
F[f * g] = F[f] F[g]
The convolution theorem also takes the alternate forms
F[fg] = F[f] * F[g]
F-1 (F[f] F[g]) = f * g
F-1(F[f] * F[g]) = f g
Q2) Explain Properties of fourier transform.
A2)
The z-transform has features that are similar to those of the Fourier transform (and Laplace transform). The only distinction is that the ROCs require extra attention. Assumptions are made in the following sections.
Z [ x[n]] = X(z) ROC = Rx
And
Z [ y[n]] = Y(z) ROC = Ry
Linearity
Z [ ax[n] + by[n]] = a X(z) + bY(z), ROC ⊇ (Rx ∩ Ry)
While it is obvious that the ROC of the linear combination of x[n] and y[n] should be the intersection of the their individual ROCs Rx ∩ Ry in which both X(z) and Y(z) exist, note that in some cases the ROC of the linear combination could be larger than Rx ∩ Ry. For example, for both x[n] = anu[n] and y[n] = anu[n-1] , the ROC is |z| > |a| , but the ROC of their difference an u[n] – anu[n – 1] = δ[n] is the entire z-plane.
Time Shifting
Z[x[n – n0]] = Z-n0 X(z), ROC = Rx
Proof:
Z[x[n – n0]] = 
Define m = n – n0, we have n = m + n0 and

The new ROC is identical to the previous one, with the exception of the possibility of adding or removing the origin or infinity, as the shift may affect the signal's duration.
Q3) Give the Example of Time Expansion (Scaling).
A3)
Example: If x[n] is ramp
n | 1 | 2 | 3 | 4 | 5 | 6 |
x[n] | 1 | 2 | 3 | 4 | 5 | 6 |
Then the expanded version x[n/2] is
n | 1 | 2 | 3 | 4 | 5 | 6 |
n/2 | 0.5 | 1 | 1.5 | 2 | 2.5
| 3 |
m |
| 1 |
| 2 |
| 3 |
x[n/2] | 0
| 1
| 0 | 2 | 0 | 3 |
Where m is the integer part of n/k.
Proof: The z-transform of a signal like this is
Z[x[n/k]] = 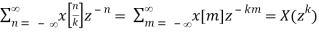
Note that the change of the summation index from n to m has no effect as the terms skipped are all zeros.
Q4) Explain Time Difference with Proof.
A4)
Z[x[n] – x[n – 1]] = (1 – z-1)X(z), ROC = Rx
Proof:
Z[x[n] – x[n – 1]] = X(z) – z-1 X(z) = (1 – z-1) X(z) = z – 1/z X(z)
Note that due to the additional zero z = 1 and pole z = 0, the resulting ROC is the same as Rx except the possible deletion of z = 0 caused by the added pole and/or addition of z = 1 caused by the added zero which may cancel an existing pole.
Q5) Explain Time Accumulation with Proof.
A5)
Z[  =
= 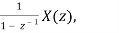 ROC ⊇ [Rx ∩ (|z| > 1)]
ROC ⊇ [Rx ∩ (|z| > 1)]
Proof: The accumulation of x[n] can be written as its convolution with u[n]:
u[n] * x[n] =  =
= 
Applying the convolution property, we get
Z[ 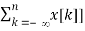 = Z[u[n] * x[n]] =
= Z[u[n] * x[n]] = 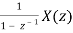
As Z[u[n]] = 
Q6) Explain Scaling in Z-domain with Proof.
A6)
Z[an x[n]] = X(z/a), ROC = |a| Rx
Proof:
Z[an x[n]] = 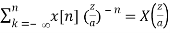
In particular, if a = ej0 , the above becomes
Z[ejn0 x[n]] = X(e-j0 z) ROC = Rx
The multiplication by e-j0 to z corresponds to a rotation by angle 0 in the z-plane, i.e., a frequency shift by 0. The rotation is either clockwise (0 > 0) or counter clockwise (0 < 0) corresponding to, respectively, either a left-shift or a right shift in frequency domain. The property is essentially the same as the frequency shifting property of discrete Fourier transform.
Q7) Explain the Example of Z-domain.
A7)
Z[nx[n]] = -z d/dz X(z), ROC = Rx
Proof:
d/dz X(z) = 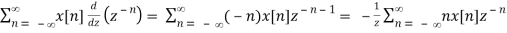
i.e.,
Z[nx[n]] = - z d/dz X(z)
Example: Taking derivative with respect to z of the right side of
Z[an u[n]] = 
We get

We have this feature of differentiation in the z-domain because of the property of differentiation in the z-domain.

Note that for a different ROC |z| < |a|, we have
Z[ - nanu [ -n – 1]] =  |z| < |a|
|z| < |a|
Q8) What is 3D Fourier Transform?
A8)
The Fourier pairs are naturally extended to three-dimensional functions as well.

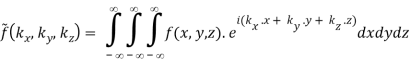
(B.39)
The 3D Fourier transform in cylindrical and spherical coordinates is then discussed.
Q9) Write a Short note on Cylindrical Coordinates.
A9)
In this case,
f(x, y, z) = g(r, θ,z)
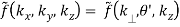
(B.40)
Where,
x + iy = r . eiθ
kx + iky =  . eiθ
. eiθ
(B.41)
The functions g and 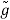 are related by
are related by
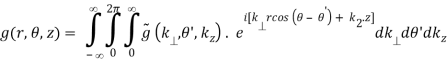
(B.42a)

(B.42b)
Under circular symmetry, i.e., f independent of θ, and 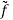 , thus, independent of
, thus, independent of 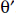 , we have
, we have
f(x, y, z) = h(r, z)
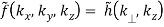
(B.43)
As a result, Eq. (B.42a-b) is formed (using the properties of the Hankel transform)
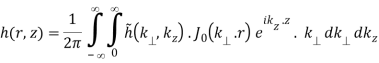
(B.44a)

(B.44b)
The integral in Eq. (B.44a) can be seen to represent a 1D Fourier transform of the Hankel transform with respect to r along z.
We have cylindrical symmetry if the problem has it, which means that f is independent of both and z.
f(x, y, z) = p(r)
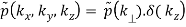
(B.45)
The Fourier transform can be reduced to
p(r) = 1/2π 
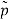 (
(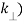 = 2π
= 2π 
(B.46)
Q10) Write a Short note on Spherical Coordinates.
A10)
In spherical coordinates,
f(x, y, z) = g(r, θ, )
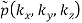 =
= 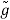 (k, θ’, ’)
(k, θ’, ’)
(B.47)
The coordinates are changed in the following way:
x = r sin θ cos , y = r sin θ sin , z = r cos θ
kx = k sin θ’ cos ’, ky = k sin θ’ sin ’, kz = k cos θ’
(B.48)
Where, again, k = 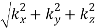 .
.
The Fourier integrals are transformed into
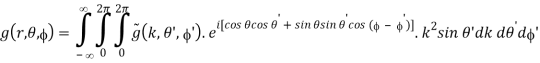

(B.49)
Under circular symmetry, i.e., f(x, y, z) is independent of , we have
f(x, y, z) = g(r, θ)

(B.50)
For circular symmetry, the Fourier transforms are
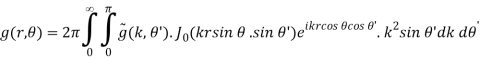
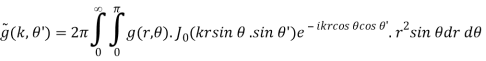
(B.51)
The function is independent of both angles for spherical symmetry, so we have
f(x, y, z) = h(r)
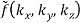 =
=  (k)
(k)
(B.52)
The integrals are reduced to in this case.
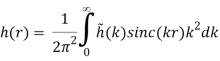

(B.53)
Q11) Write the Application of Fourier transform to differential equation.
A11)
The solution of differential equations can also be done using Fourier Transforms. To demonstrate this concept, we'll go over an Ordinary Differential Equation (ODE) and see how the Fourier Transform can be used to solve a differential equation.
Take a look at the ODE in Equation [1]:
d2y(t)/dt2 – y(t) = - g(t) [Equation 1]
The function y(t) that satisfies Equation [1] is what we're looking for. Why not take the Fourier Transform of an equation? We can take the Fourier Transform of a function, so why not an equation? It turns out there's no reason why we shouldn't be able to. Because the Fourier Transform is a linear operation, the time domain produces an equation in which each term corresponds to a frequency domain term. Equation [2] is obtained by applying the Fourier Transform to Equation [1]:
F{d2y(t)/dt2 } – F{ y(t)} = F{- g(t)} [Equation 2]
F{d2y(t)/dt2 } – Y(f) = - G(f)
If you recall the Fourier Transform's differentiation property, we can see that derivatives in the time domain become simple multiplication in the frequency domain:
F{dy(t)/dt} = (2πif)Y(f)
F{d2y(t)/dt2} = (2πif)2 Y(f). . . [Equation 3]
F{dny(t)/dtn} = (2πif)n Y(f)
Hence, Equation [2] becomes:
(2πif)2 Y(f) – Y(f) = - G(f) [Equation 4]
For Y(f), equation [4] is a simple algebraic equation! This is a simple problem to solve. The following is an example of how Fourier Transforms can be used to solve differential equations: They can solve algebraic equations by converting differential equations.
For Y(f), equation [4] can be easily solved:
Y(f) = -G(f)/(2πif)2 – 1 = G(f)/ 1+ 4π2f2 [Equation 5]
Q12) Explain 1D Wave Equation.
A12)
Consider problem
utt = c2uxx, - < x < , (32)
u|t=0 = g(x), (33)
ut|t=0 = h(x). (34)
We arrive at by performing a partial Fourier transform with respect to x.



Then characteristic equation for ODE (3535) is α2 = - c2 2 and α1,2 = ± ic
2 and α1,2 = ± ic
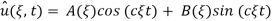
With initial conditions implying A(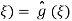 ,
, 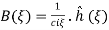 and
and

Rewriting 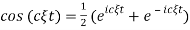 and recalling that multiplication of FT by
and recalling that multiplication of FT by 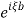 is equivalen to to shifting original to the left by b we conclude that
is equivalen to to shifting original to the left by b we conclude that  is a Fourier transform of ½ (g(x+ct) + g(x – ct))
is a Fourier transform of ½ (g(x+ct) + g(x – ct))
If we denote H as a primitive of hh then 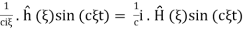 which in virtue of the same arguments is FT of
which in virtue of the same arguments is FT of 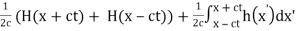
Therefore
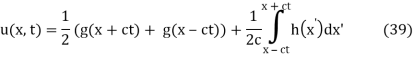
We've returned to the d'Alembert formula.
Q13) What is Heat Equation?
A13)
Consider problem
ut = kuxx, t > 0, - < x < , (1)
u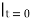 = g(x) (2)
= g(x) (2)
Making partial Fourier transform with respect to x↦ξ (so u(x,t)↦u^(ξ,t)) we arrive to


Indeed, ∂x↦iξ and therefore ∂2 x↦−ξ2
Note that (3) is an ODE and solving it we arrive to
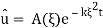 ; plugging into (4) we find that A(ξ) =
; plugging into (4) we find that A(ξ) = 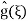 and therefore
and therefore
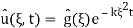
The right-hand expression is a product of two Fourier transforms, one is 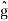 (ξ) and another is Fourier transform of IFT of e−kξ2te
(ξ) and another is Fourier transform of IFT of e−kξ2te
If we had  we would have IFT equal to
we would have IFT equal to  but we can get from
but we can get from 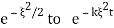 by scaling
by scaling 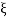 ↦ (2kt)-1/2
↦ (2kt)-1/2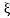 and therefore x ↦ (2kt)-1/2x (and we need to multiply the result by (2kt)-1/2 ; therefore
and therefore x ↦ (2kt)-1/2x (and we need to multiply the result by (2kt)-1/2 ; therefore 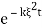 is a Fourier transform of
is a Fourier transform of 
Again: 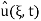 is a product of FT of g and of
is a product of FT of g and of  and therefore uu is the convolution of these functions (multiplied by 1/(2π)):
and therefore uu is the convolution of these functions (multiplied by 1/(2π)):
u(x, t) = g * 1/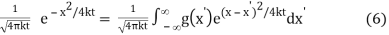
We recovered formula which we had already.