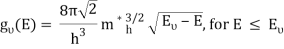Unit - 3

Quantum Statistics

Q1) Explain Macrostates and microstates.

A1)

A microstate, for example, defines the position and momentum of each particle in a classical system of point particles. It determines the value of the wavefunction at every point in space in a quantum mechanical system. You must give the most thorough description you will ever care about to define what microstate the system is in.

You might be thinking if this is a reasonable assumption. What if there aren't any discrete microstates? A classical particle's position and momentum, for example, are continuous rather than discrete. At its most fundamental level, the question of whether the cosmos is discrete or continuous remains unanswered. Fortunately, this turns out not to matter very much. You can always turn a continuous variable into a discrete one by dividing it into very small bins. For the classical particle, we treat all positions between xx and x+δx and all momenta between pp and p+δp as a single microstate. As long as we choose δx and δp sufficiently small, the exact values turn out to have no effect on most of our results.

This is depicted in Figure, which depicts the space of possible microstates in one dimension for a single particle. The values of x and p define each microstate. This is known as phase space, and we'll be using it a lot. A 2dN dimensional phase space exists for a system of N particles in dddimensions. In this phase space, each point represents a microstate.

Each axis is segmented into very small intervals. A microstate is a volume defined by the intersection of one interval from each axis.

The number of microstates in ordinary systems is enormous, and they characterise the system in far more detail than humans generally care about. Consider the case of a gas-filled box. You have no means of knowing the exact position and momentum of every single gas molecule, and even if you could, you wouldn't care. Instead, you're usually just concerned with a few macroscopic variables: the system's total energy, the total number of gas molecules, the volume of space it occupies, and so on. These are things that can be measured and are useful in the real world.

The value of each macroscopic variable is used to define a macrostate. It's possible that a large number of microstates belong to the same macrostate. Let's say you want to calculate the total energy and volume of a box of gas. There are a huge variety of different configurations of individual gas molecules that sum up to that amount of energy and volume. You're quite sure the gas is in one of those states, but you're not sure which one.

Q2) Explain Fermions and Bosons statement.

A2)

Fermions

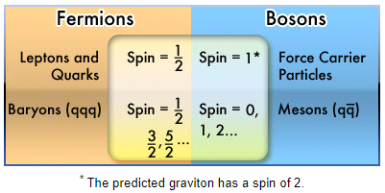
Any particle with an odd half-integer spin (such as 1/2, 3/2, and so on) is called a fermion. Fermions include quarks and leptons, as well as most composite particles like protons and neutrons.

The odd half-integer spin has the unintended consequence of obeying the Pauli Exclusion Principle, which means fermions cannot exist in the same state at the same time for reasons we don't fully comprehend.

Bosons

The particles with an integer spin are known as bosons (0, 1, 2...).

All force carrier particles, as well as composite particles containing an even number of fermion particles, are bosons (like mesons).

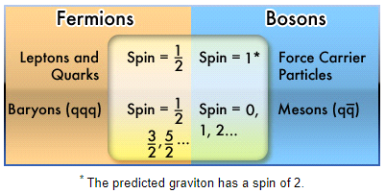
Depending on whether the total number of protons and neutrons in an atom is odd or even, the nucleus is a fermion or a boson. Physicists recently discovered that this has resulted in some odd behaviour in particular atoms under extraordinary settings, such as extremely cold helium.

Q3) What's The Difference Between A Fermion And A Boson?

A3)

In the entire Universe, there are only two types of fundamental particles: fermions and bosons. Every particle possesses an intrinsic quantity of angular momentum, often known as spin, in addition to the usual attributes such as mass and electric charge. Fermions are particles with spins in half-integer multiples (e.g., 1/2, 3/2, 5/2, etc.) while bosons are particles with spins in integer multiples (e.g., 0, 1, 2, etc.). In the entire known Universe, there are no other forms of particles, basic or composite. But why is this significant? The following is a question from an anonymous reader:

At first look, it may appear that classifying particles based on these characteristics is utterly arbitrary.

The Standard Model's known particles. This is a list of all the fundamental particles that have been discovered... [plus]

SIEGEL, E.

After all, isn't a particle just a particle? Surely there are more differences between quarks and leptons (which do not experience the strong force) than there are between fermions and bosons? Surely there's more to the difference between matter and antimatter than your particle's spin? And whether you're gigantic or massless should be a major concern, right? Especially when compared to something like angular momentum, right?

As it turns out, there are a number of little changes in spin that matter, but there are two major ones that impact far more than most people, including physicists, understand.

The photons, particles and antiparticles of the early Universe. It was filled with both bosons and... [+]

Q4) Write a short note on Andrew Deniszczyc.

A4)

You may also form composite particles out of fermions: a proton (which is a fermion) is made up of two up quarks and one down quark, whereas a neutron is made up of one up and two down quarks (also a fermion). Because of how spins function, if you bind an odd number of fermions together, your new (composite) particle will behave like a fermion, which is why protons and antiprotons exist, and why a neutron differs from an antineutron. However, particles made up of an even number of fermions, such as a quark-antiquark pair (known as a meson), act like a boson. The neutral pion (π0), for instance, is its own antiparticle.

The reason behind this is simple: each of those fermions is a spin ±1/2 particle. If you add two of them together, you can get something that's spin -1, 0, or +1, which is an integer (and hence a boson); if you add three, you can get -3/2, -1/2, +1/2, or +3/2, As a result, it's a fermion. As a result, particle/antiparticle differences are significant. However, there is a second distinction that is arguably much more significant.

Fig. The electron energy levels of a neutral oxygen atom in the lowest feasible energy configuration.

Q5) What is foundation and adrignola of wikimedia commons.

A5)

Only fermions, not bosons, are excluded under the Pauli exclusion principle. This rule expressly asserts that no two fermions can occupy the same quantum state in any quantum system. Bosons, on the other hand, are unrestricted. When you add electrons to an atomic nucleus, the first electron will tend to inhabit the ground state, which is the lowest energy state possible. The spin state of that electron can be either +1/2 or -1/2 because it's a spin=1/2 particle. If you add another electron to that atom, it must have the opposite spin state in order to be in the ground state as well.  They can no longer fit in the ground state and must progress to the next energy level.

Within a hydrogen atom, the energy levels and electron wavefunctions that correspond to different states... [+]

Q6) Write a short note on Poorleno Of Wikimedia Commons And Jenny Mottar.

A6)

POORLENO OF WIKIMEDIA COMMONS:

That is why the periodic table is set up the way it is. This is why atoms have diverse properties, why they bond together in such complex ways, and why each element in the periodic table is distinct: each type of atom has a different electron configuration than the others. The physical and chemical properties of the elements, the vast variety of molecular configurations we have today, and the basic bonds that allow complex chemistry and life to exist are all due to the fact that no two fermions can occupy the same quantum state.

The way atoms join together to form compounds, such as organic compounds and biological activities,... [+]

JENNY MOTTAR

On the other side, you can put as many bosons in the same quantum state as you want! This enables the production of Bose-Einstein condensates, which are extremely rare bosonic states. You can put any number in there by cooling bosons sufficiently such that they fall into the lowest energy quantum state. At low enough temperatures, helium (which is made up of an even number of fermions and hence acts like a boson) becomes a superfluid as a result of Bose-Einstein condensation. Gases, molecules, quasi-particles, and even photons have all been condensed since that time. It's still a hot topic of study today.

Before (L), during (Middle), and after (R) the... [+] A Bose-Einstein condensate of rubidium atoms before (L), during (Middle), and after (R) the…

Q7) Introduce the Bose Einstein distribution function and Fermi –Dirac distribution function.

A7)

The probability density functions, also known as distribution functions, represent the likelihood that particles would occupy the available energy levels in a particular system. While the actual derivation belongs in a statistical thermodynamics course, understanding the underlying assumptions of such derivations, and hence the applicability of the results, is of importance.

The derivation begins with the premise that each potential particle distribution over the available energy levels has the same probability as any other potential distribution that can be separated from the first.

Furthermore, one considers the fact that both the total number of particles and the total energy of the system have a particular value.

Third, one must recognise that various particles behave differently. At any given energy level, only one Fermion can exist (as described by a unique set of quantum numbers including spin). There is no limit to the number of bosons that can occupy the same energy levels. Fermions and bosons have the same "appearance," that is, they are indistinguishable. It is possible to differentiate Maxwellian particles from one another.

Using the Lagrange method of indeterminate constants, the derivation then produces the most likely particle distribution. One of the Lagrange constants, the average energy per particle in the distribution, turns out to be a more important physical quantity than the total energy. The Fermi energy, or EF, is the name for this variable.

The fact that one is dealing with a high number of particles is an important assumption in the derivation. This assumption allows the Stirling approximation to be used to approximate the factorial terms.

The resulting distributions have several unusual properties that are difficult to explain. First and foremost, regardless of whether a specific energy level exists or not, a probability of occupancy can be calculated. Since the density of possible states defines where particles can be in the first place, it seems more reasonable that the distribution function is dependent on it.

The assumption that a given energy level is in thermal equilibrium with a large number of other particles causes the distribution function to be independent of the density of states. It is unnecessary to go into detail on the nature of these particles because their number is so large. The density of states' independence is advantageous since it gives a single distribution function for a wide range of systems.

The image below shows a plot of the three distribution functions, the Fermi-Dirac distribution, the Maxwell-Boltzmann distribution, and the Bose-Einstein distribution, with the Fermi energy set to zero.

The Fermi-Dirac (red curve), Bose-Einstein (green curve), and Maxwell-Boltzman (blue curve) distributions show occupancy probability versus energy.

For large energies, the three distribution functions are nearly equivalent (more than a few kT beyond the Fermi energy). For energies a few kT below the Fermi energy, the Fermi-Dirac distribution reaches a maximum of 1, whereas the Bose-Einstein distribution diverges at the Fermi energy and has no validity for energies below the Fermi energy.

Q8) State the Fermi-Dirac distribution function.

A8)

The Fermi-Dirac probability density function calculates the likelihood of a Fermion in thermal equilibrium with a large reservoir occupying a certain energy level. Fermions are particles that have a half-integer spin (1/2, 3/2, 5/2, etc.). The Pauli exclusion principle asserts that only one Fermion can occupy a state specified by its set of quantum numbers n,k,l, and s. This is a unique property of Fermions. As a result, Fermions could alternatively be defined as particles that follow the Pauli exclusion principle. All of these particles have a half-integer spin as well.

Both electrons and holes have a spin of 1/2 and follow Pauli's exclusion principle. These particles will fill the available states in an energy band when they are added to it, just like water fills a bucket. The lowest-energy states are filled first, followed by the next higher-energy levels. The energy levels are all filled up to a maximum energy, which we call the Fermi level, at absolute zero temperature (T = 0 K). There are no states filled above the Fermi level. The transition between entirely filled and completely empty states is gradual rather than sudden at higher temperatures. This behaviour is described by the Fermi function, which is:

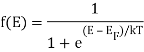
Q9) Define Bose- Einstein Condensation.

A9)

The exotic quantum phenomena of Bose-Einstein condensation was first detected in dilute atomic gases in 1995, and it is currently the focus of extensive theoretical and experimental research.

The cloverleaf magnetic trap at MIT is set up for evaporative cooling. Axial confinement is provided by the middle (curvature) coils, while radial confinement is provided by the outside coils (the "clover leaves" or gradient coils). Cigar-shaped clouds are formed as a result of the anisotropic potential. The most energetic atoms' spins are preferentially flipped by radio-frequency radiation from an antenna, while the remainder atoms rethermalize to a lower temperature. The radio-frequency is lowered to force cooling.

Satyendra Nath Bose, an Indian physicist, wrote Einstein a paper in 1924 in which he calculated the Planck rule for black-body radiation by treating photons as a vapour of identical particles. In the same year, Einstein extended Bose's theory to an ideal gas of identical atoms or molecules, in which the number of particles is conserved, and predicted that the particles would get trapped together in the system's lowest quantum state at sufficiently low temperatures. We now know that Bose-Einstein condensation (BEC) occurs only for “bosons” — particles having a total spin that is an integer multiple of h, the Planck constant divided by 2 pi.

This Bose condensate, as well as the condensation process itself, was predicted to exhibit a variety of odd features, and scientists have been attempting to create Bose-Einstein condensation in the laboratory for years. Finally, in 1995, researchers from the Massachusetts Institute of Technology (MIT) and JILA, a laboratory maintained by the National Institute of Standards and Technology and the University of Colorado in Boulder, Colorado, uncovered convincing evidence for Bose-Einstein condensation in dilute atomic gases.

Since then, the Boulder and MIT teams, as well as a team at Rice University in Houston, Texas, have refined the procedures for making and studying this unique quantum phenomena, and rapid progress has been made in understanding its dynamic and thermodynamic features. At MIT, we recently confirmed the fascinating property of Bose-condensed atoms being "laser-like" — that is, that the atoms' matter waves are coherent. We were able to observe coherence directly in these experiments, and we developed a crude "atom laser" that generates a beam of coherent atoms, similar to how an optical laser emits coherent photons. Simultaneously, theorists have addressed a number of fundamental difficulties and devised effective ways for simulating real-world systems.

Q10) Describe the Order reigns in the ground state as per Bose- Einstein Condensation.

A10)

The dynamical behaviour of a gas at room temperature is not affected by the fact that one atom cannot be distinguished from another. In accordance with the Heisenberg uncertainty principle, the position of an atom is smeared out over a distance given by the thermal de Broglie wavelength, lambdadB = (2 pi h-bar2 / kBmT)1/2, where kB is the Boltzmann constant, m is the atomic mass and T is the temperature of the gas. At room temperature the de Broglie wavelength is typically about ten thousand times smaller than the average spacing between the atoms. This means that the matter waves of the individual atoms are uncorrelated or “disordered”, and the gas can thus be described by classical Boltzmann statistics.

As the gas is cooled, however, the smearing increases, and eventually there is more than one atom in each cube of dimension lambdadB. The wavefunctions of adjacent atoms then “overlap”, causing the atoms to lose their identity, and the behaviour of the gas is now governed by quantum statistics.

Bose-Einstein statistics dramatically increase the chances of finding more than one atom in the same state, and we can think of the matter waves in a Bose gas as “oscillating in concert”. The result is Bose-Einstein condensation, a macroscopic occupation of the ground state of the gas. (In contrast, fermions – particles with a total spin of (n + ½)h, where n is an integer – cannot occupy the same quantum state.) Einstein described the process as condensation without interactions, making it an important paradigm of quantum statistical mechanics.

The density distribution of the condensate is represented by a single macroscopic wavefunction with a well defined amplitude and phase, just as for a classical field. Indeed, the transition from disordered to coherent matter waves can be compared to the change from incoherent to laser light.

Q11) Define the term Chilling the atoms.

A11)

Bose-Einstein condensation has been cited as an important phenomenon in many areas of physics, but until recently the only evidence for condensation came from studies of superfluid liquid helium and excitons in semiconductors. In the case of liquid helium, however, the strong interactions that exist in a liquid qualitatively alter the nature of the transition. For this reason a long-standing goal in atomic physics has been to achieve BEC in a dilute atomic gas. The challenge was to cool the gases to temperatures around or below one microkelvin, while preventing the atoms from condensing into a solid or a liquid.Efforts to Bose condense atoms began with hydrogen more than 15 years ago. In these experiments hydrogen atoms are first cooled in a dilution refrigerator, then trapped by a magnetic field and further cooled by evaporation (see below). This approach has come very close to observing BEC, but is limited by the recombination of individual atoms to form molecules and by the detection efficiency. In the 1980s laser-based techniques such as Doppler cooling, polarization-gradient cooling and magneto-optical trapping were developed to cool and trap atoms. These techniques profoundly changed the nature of atomic physics and provided a new route to ultracold temperatures that does not involve cryogenics. Atoms at sub-millikelvin temperatures are now routinely used in a variety of experiments. Alkali atoms are well suited to laser-based methods because their optical transitions can be excited by available lasers and because they have a favourable internal energy-level structure for cooling to low temperatures. However, the lowest temperature that these laser cooling techniques can reach is limited by the energy of a single photon. As a result, the “phase-space density” – the number of atoms within a volume lambdadB3 – is typically about a million times lower than is needed for BEC.

The successful route to BEC turned out to be a marriage of the cooling techniques developed for hydrogen and those for the alkalis: an alkali vapour is first laser cooled and then evaporatively cooled. In evaporative cooling, high-energy atoms are allowed to escape from the sample so that the average energy of the remaining atoms is reduced. Elastic collisions redistribute the energy among the atoms such that the velocity distribution reassumes a Maxwell-Boltzmann form, but at a lower temperature. This is the same evaporation process that happens when tea cools, but the extra trick for trapped atoms is that the threshold energy can be gradually lowered. This allows the atomic sample to be cooled by many orders of magnitude, with the only drawback being that the number of trapped atoms is reduced.

The challenge in combining these two cooling schemes for alkalis was a question of atomic density. Optical methods work best at low densities, where the laser light is not completely absorbed by the sample. Evaporation, on the other hand, requires high atomic densities to ensure rapid rethermalization and cooling. This changed the emphasis for optical methods: while they had previously been used to produce low temperatures and high phase-space density simultaneously, they now needed to produce high elastic collision rates. Furthermore, this had to be achieved in an ultrahigh vacuum chamber to prolong the lifetime of the trapped gas. Thus no new concept was needed to achieve BEC, but rather it was an experimental challenge to improve and optimise existing techniques. These developments were pursued mainly at MIT and Boulder from the early 1990s.

Q12) Define the Improved techniques in magnetic trapping.

A12)

For evaporative cooling to work, the atoms must be thermally isolated from their surroundings. This must be done with electromagnetic fields, since at ultracold temperatures atoms stick to all surfaces. The best method for alkalis is magnetic confinement, which takes advantage of the magnetic moment of alkali atoms. After the atoms are trapped and cooled with lasers, all light is extinguished and a potential is built up around the atoms with an inhomogeneous magnetic field. This confines the atoms to a small region of space.

Atoms can only be cooled by evaporation if the time needed for rethermalization is much shorter than the lifetime of an atom in the trap. This requires a trap with tight confinement, since this allows high densities and hence fast rethermalization times. For this reason, the first experiments that observed BEC used so-called linear quadrupole traps, which have the steepest possible magnetic fields. At MIT, dispersive light scattering (phase-contrast imaging) was used to observe the development of a Bose condensate in a direct and non-destructive way. The intensity of dispersed light is plotted as a function of trap position, which is proportional to the atom column density along the line of sight. The cloud has been cooled to just above the BEC transition temperature in the figure on the left, and the atom distribution is practically classical. A strong peak of atoms appears at the trap centre (middle) as the temperature is decreased across the phase transition, and further cooling increases the condensate fraction to nearly 100%. (right).

These approaches do create great densities and rapid evaporation, but they have one fundamental flaw: the magnetic field at the centre is zero, causing an atom to become "disoriented" and lose its magnetic moment's alignment. These "spin flips" result in a calamitous loss of atoms from the trap since a magnetic field can only confine atoms with magnetic moments that are antiparallel to the field. Both the Boulder and MIT teams devised solutions to the challenge. A rotating magnetic field was created by the Boulder group to keep the atoms away from the "hole," while we "plugged" the hole using the repulsive force of a focused laser beam.

Both of these methods were successful, yet they both had significant flaws. We discovered BEC in an unique "cloverleaf" magnetic trap that overcome these restrictions in March 1996. This trap is a modification of the Ioffe-Pritchard trap, which was first proposed in 1983 and contains a non-zero magnetic field at its centre to prevent atom loss. The confinement is tight in two directions but weak in the third, resulting in cigar-shaped trapped clouds rather than spherical trapped clouds. The trap's unique feature is the coils' "cloverleaf" winding arrangement, which provides good optical access to the sample for laser cooling and trapping, as well as probing the condensate (see figure 1). The trap's design has proven to be dependable and versatile, and it was used to gather the majority of the experimental results shown here. Given the amount of effort that has gone into trap design in recent years, it's remarkable that the best setup has been around for almost 13 years.

Using electron spin resonance, evaporation can be easily accomplished in a magnetic trap. Applying a radio-frequency field in resonance with the energy difference between the spin-up and spin-down states flips the magnetic moments of trapped atoms. The field's frequency is set such that it only impacts the atoms at the cloud's edge, which have the most energy in a harmonic oscillator potential. The magnetic forces become anti-trapping and the atoms are freed from the trap when the moments of these atoms are inverted. Because the cloud cools and shrinks towards the trap's centre, the frequency of the radio-frequency field must be decreased to keep evaporation at the cloud's perimeter.

In our trials, sodium atoms are ejected from an oven at 600 K (800 m s-1) and a density of around 1014 cm-3. The atoms are initially slowed to a speed of roughly 30 m s-1 over a distance of 0.5 m using a laser beam. Around 1010 atoms can be trapped in a magneto-optical trap at this speed. The temperature of the gas is reduced to roughly 100 K using laser cooling and trapping techniques, which is cold enough for the atoms to be trapped with magnetic fields. In about 20 seconds, evaporation cools the gas to about 2 K, the temperature at which a condensate develops.

Q13) What is meant by Observing condensation.

A13)

Condensates trapped in the trap are very tiny and optically thick, making them difficult to see. By turning off the trap and letting the atoms to expand ballistically, the first observations of BEC were made. After that, a laser beam in resonance with an atomic transition was flashed on, and the subsequent light absorption generated a "shadow" that was captured by a camera. This picture of atomic locations records the velocity distribution of the atoms since they were released from the trap. Because the atoms in the condensate are in the lowest energy state, they expand very little, and the dramatic mark of Bose condensation was thus the abrupt development of a prominent peak of atoms in the image's centre.

Because the atoms are freed from the trap, absorption imaging is fundamentally destructive. Furthermore, the atoms are heated by the absorbed photons. In early 1996, we used "dark-ground" imaging, a technique that depends on dispersion rather than absorption, to examine a Bose condensate non-destructively.

A complicated index of refraction can be used to characterise both dispersion and absorption. The absorption of photons from the probe beam is described by the imaginary part of the index, which is followed by inelastic scattering of light over high angles. Coherent elastic scattering over small angles corresponds to the real part. The phase of the light is altered by dispersive scattering, and because the light is only slightly deflected, the technique is nearly non-perturbative. The crucial point is that if the probing laser is detuned far enough away from any atomic resonances, dispersive scattering dominates absorption, and the condensate resembles a piece of shaped glass, or a lens.

The phase shift induced by the atoms must be converted into an intensity variation in order to “see” the condensate using dispersive scattering. This is a well-known optical problem that can be solved by spatial filtering. Opaque objects (“dark-ground imaging”) or phase-shifters (“phase-contrast imaging”) are used to alter the signal in the Fourier plane.

Because dispersive imaging is non-destructive, many photographs of the same condensate can be acquired. Figure 2 shows phase-contrast imaging of the development of a condensate. Such real-time pictures will be essential in researching a condensate's dynamical behaviour.

Q14) What is Realization of a basic atom laser.

A14)

The possibility of producing a coherent beam of atoms, which could be collimated to travel large distances or brought to a tiny focus like an optical laser, has sparked the imagination of atomic physicists. Such an atom laser could have a major impact on the fields of atom optics, atom lithography and precision measurements.

A Bose-Einstein condensate is a sample of coherent atomic matter and is thus a good starting point for an atom laser. The process of condensing atoms into the ground state of a magnetic trap is analogous to stimulated emission into a single mode of an optical laser and one can think of the trap as a resonator with “magnetic mirrors”. An important feature of a laser is an output coupler to extract a fraction of the coherent field in a controlled way, and at MIT we recently demonstrated such a device for a trapped Bose gas.

The tiny, straight striations have a period of 15 m and are fringes caused by matter-wave interference. The ballistic expansion from a harmonic double-well potential is responsible for the significantly bigger modulations in the cloud structure.

Because a magnetic trap can only confine atoms with magnetic moments that are antiparallel to the magnetic field, we changed the “reflectivity” of the magnetic mirrors by tilting the atoms' magnetic moments using a short radio-frequency pulse. The atoms were removed in this manner, accelerated under gravity, and absorption imaging was used to examine them. The extracted fraction may be changed between 0% and 100% by altering the amplitude of the radio-frequency field (see Physics World 1996 October p18).

The coherence of a laser's output, or the presence of a macroscopic wave, is an important aspect. Coherence has been utilised as a defining condition for BEC in theoretical treatments. However, none of the measurements detailed thus far have shown long-range order. Although collective measurements match with Schrödinger equation solutions at zero temperature, identical frequencies have been anticipated for a classical gas in the hydrodynamic regime.

Examining the impacts of the phase of the condensate wavefunction is one way to explore coherence. The Josephson effect has been used to see this phase in superconductors, and the motion of quantized vortices in liquid helium has been used to infer it. Because phase is a complex number, it can only be recognised as an interference effect between two different wavefunctions, similar to how interference between two independent laser beams may be detected. Theoretical work on coherence and the interference features of confined Bose gases has recently gotten a lot of interest. The theoretical issues that lie beneath are of great interest and concern. For example, can spontaneous symmetry breaking (an important topic in physics) apply in systems with few atoms, and what impact do particle-particle interactions have on the phase of the condensate.

We recently witnessed high-contrast interference of two separate Bose condensates at MIT, demonstrating that a condensate has a well-defined phase. By concentrating a sheet of light into the cloverleaf trap and repelling atoms from the centre, we created a double-well trapping potential. Evaporation resulted in the formation of two distinct condensates. These were left to free-fall and expand ballistically under gravity.

The clouds overlapped horizontally after lowering 1 cm, and absorption revealed the interference pattern (figure 6). The fringes have a period of 15 p.m., which matches the respective de Broglie wavelengths of the overlapping clouds. When the imaging system's resolving power is taken into account, the intensity difference between the light and dark fringes indicate that the atomic interference modulation was between 50% and 100%. Figure 6 has the unique feature of being a real-time snapshot showing interference. The wavefront of a single particle is separated and then recombined in classic experiments to demonstrate the wave aspect of matter, and this is repeated numerous times to build up an interference pattern.

Q15) How to see Planck's radiation law as a consequence of Bose Einstein statistics?

A15)

Planck's law is the result of the following factors.

1) The mode density per unit volume in a cavity is 8πυ2/c3.

2) Within each mode, assume Boltzmann statistics i.e the probability of having an energy E is given by p(E) ∝ e-E/kT

3) Ask that the energies E be discretized as nhν instead of continuous. Essentially, the difference between doing 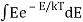 and the sum 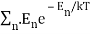, where  gives Planck's law.

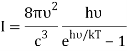
So far, it's a nice trick to go to the discrete sum but that's all that was done. There is no sense in which the particles are indistinguishable etc.

What is the correct modern way of seeing this result? I assume the starting point is that we have an ideal gas of photons inside a blackbody cavity and they follow statistics that yield 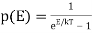 but how exactly does one go from there to Planck's law?

As you mentioned, we use a cavity as a model for blackbody radiation, for which you have already determined the mode density.

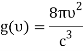
The photons' energies are discretized and have the formula E=nhv, where nn is an integer. The grand-canonical partition function for bosons with vanishing chemical potential will now be written down. Because photons interact with the cavity's walls, the number of photons isn't constant, it's taken to be zero. For a given frequency 0 the partition function is The energies that photons can have are discretized and have the formula E=nh, where nn is a positive integer. The grand-canonical partition function for bosons with vanishing chemical potential will now be written down. Because photons interact with the cavity's walls, the number of photons isn't constant, it's taken to be zero. For a given frequency 0 the partition function is

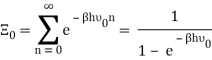
The total partition function can then be obtained by multiplying all of the frequency partition functions together.

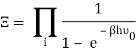
Taking the logarithm of ΞΞ will transform the product in a sum

Which can be modified in an integral if the difference in frequency between two consecutive frequencies becomes minuscule. We can delegate this task to the density of modes g(v) instead of counting the number of photons per frequency:

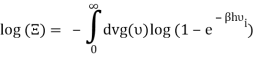
You can now calculate the energy associated using 

So

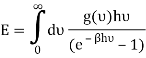
And from the relation 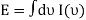  you find that

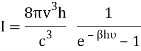
Q16) Write Bose deviation from Planck’s law.

A16)

According to Max Planck,19–21 a blackbody is a collection of numbers of oscillators. An oscillator emits or absorbs energy proportional to its oscillation frequency. Thus, emission or absorption of energy of a blackbody is discrete rather continuous which is termed as quantization of energy. This concept of quantization of electromagnetic radiation is used to explain the energy density distribution nature of a blackbody.

On the other hand, Louis de Broggle proposed that every moving object has a wave-particle dual character.12 According to the de Broggle, wavelength (λ) of a particle having momentum p, is hphp, where h is the Planck’s constant. Since oscillators are in motion and have momentum, they should have de Broggle wavelength.

Following Planck’s postulate,22 let us consider that the number of identical resonators per unit volume of a blackbody, having oscillation frequency ν, is N at the equilibrium temperature (T). If U is the vibrational energy of a resonator, the total energy per unit volume is NU. It is known that the rate of change of vibrational entropy, S, with respect to the change of vibrational energy, U, at a temperature T is –

If Ni number of particles occupy the ith vibrational state, the total energy of these particles are

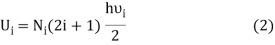
For frequency vi, the number of modes per unit volume is 82ic38i2c3. In this case, the total energy per unit volume for this frequency is calculated using the equipartition principle (classical technique).

Comparing Equation (2) and (3) we get an expression for the number of particles at ith vibrational state which is

Where v0 is the ground state vibrational energy's frequency. Equation can be used to compute a system's total internal energy (U) (4). The total energy per unit volume (U) of a system is equal to the number of particles per unit volume (N).

From Equation (5) we get

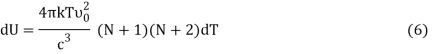
Or,

DU = BkdT                                                                                                              (7)

Where,

Putting the value of dU in Equation (1) we get

DS = Bkd (ln T)                                                                       (9)

On the integration of Equation (9), we get

S = Bkln T                                                                                  (10)

Because, for an ideal system, entropy is zero at 0K according to the third law of thermodynamics. It is also known that the thermal entropy is zero at the Bose-Einstein Condensate temperature.23,24

Following the Planck’s derivation22 of the entropy of an oscillator, we get

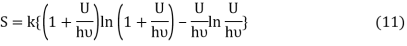
Where ν is the frequency of the oscillator. Equation (11) may be rearranged as

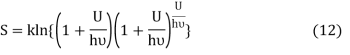
Comparing equation (10) and equation (12) we get

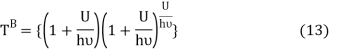
Equation (13) is also valid for ν0. If T0K is the Bose-Einstein condensate temperature of the system, then at T0K temperature all the oscillators should exist in the ground vibrational state. Thus, from Equation (13) we get

From equation (5) we get

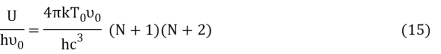
Let,

Where,

Putting this value of Uhν0Uhν0 in equation (14) we get the Bose-Einstein condensate temperature of the system of interest in terms of Z and B, which is

It is impossible to find the value of T0 unless Z and B are known. But, we can study the variation of T0 with the changes of Z and B.

Q17) Effect of temperature on Fermi –Dirac distribution function.

A17)

The electrons have little energy and hence inhabit lower energy states at T = 0 K. The Fermi-level is the highest energy state among these inhabited levels. As a result, electrons do not occupy any energy levels above the Fermi level. As a result, as indicated by the black curve in Figure 2, we get a step function that defines the Fermi-Dirac distribution function.

However, when the temperature rises, the electrons gather more and more energy, eventually reaching the conduction band. As a result, at higher temperatures, it is difficult to discriminate between the occupied and unoccupied states, as seen by the blue and red curves in Figure 2.

The free electrons in a solid crystal have different energies. According to quantum theory, free electrons continually occupy distinct energy levels at absolute zero temperature, with no gaps between filled states. Dropping the free electrons of a metal one by one into the potential well demonstrates this. The first electron to be dropped would occupy the lowest accessible energy level, say E0, and the following electron would do the same. The following energy level would be occupied by the third electron. Because of Pauli's exclusion principle, the third electron dropped would occupy the energy level E1 (>E0), and so on. If there are N (even) electrons in the metal, they will be dispersed in the first N/2 energy levels, with the higher energy levels being completely empty.

Distribution of electrons in various energy levels at 0 K.

The highest filled level, which separates the filled and empty levels at 0 K is known as the Fermi level and the energy corresponding to this level is called Fermi energy (EF). Fermi energy can also be defined as the highest energy possessed by an electron in the material at 0 K. At 0 K, the Fermi energy EF is represented as EF0. As the temperature of the metal is increased from 0 K to TK, then those electrons which are present up to a depth ofKBT from Fermi energy may take thermal energies equal to KBT and occupy higher energy levels, whereas the electrons present in the lower energy levels i.e., below KBT from Fermi level, will not take thermal energies because they will not find vacant electron states.

The probability that a particular quantum state at energy E is filled with an electron is given by Fermi-Dirac distribution function f(E), given by:

A graph has been plotted between f(E) and E, at different temperatures 0 K, T1 K, T2 K, T3 K.

Analytical Treatment At 0 K: Substitute T = 0 K in the Fermi-Dirac distribution, we have

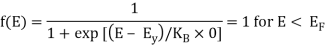
= 0 for E > EF

The curve has step-like character with f(E) = 1 for energies below EF0 and f(E) = 0 for energies above EF0. This represents that all the energy states below EF0 are filled with electrons and all those above it are empty.

At T > 0 K

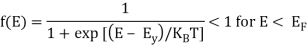
> 0 for E > EF

= ½ for E = EF

As the temperature is raised from absolute zero to T1K, the distribution curve begins to departs from step-like function and tails off smoothly to zero. Again with a further increase in temperature to T2K and to T3K, the departure and tailing of the curves increases. This indicates that more and more electrons may occupy higher energy states with an increase of temperature and as a consequence the number of vacancies below the Fermi level increases in the same proportion. At non-zero temperatures, all these curves pass through a point whose f(E) =1/2, at E = EF . So EF lies half way between the filled and empty states.

Q18) Define Degenerate Fermi gas.

A18)

In physics, a degenerate gas is a particular configuration of a gas made up of subatomic particles with half-integral intrinsic angular momentum that is frequently obtained at high densities (spin). Fermions are particles whose microscopic behaviour is governed by a set of quantum mechanical principles known as Fermi-Dirac statistics (q.v.). These principles specify, for example, that any quantum-mechanical state of a system can only have one fermion. Because the lower-energy states have all been filled, the extra fermions are forced to inhabit states of higher and higher energy as particle density rises. The pressure of the fermion gas rises as the higher-energy states gradually fill in, a phenomenon known as degeneracy pressure. A fully degenerate, or zero-temperature, fermion gas is one in which all of the energy levels below a certain value (named Fermi energy) are filled. All fermions, including electrons, protons, neutrons, and neutrinos, follow Fermi-Dirac statistics. Degenerate electron gas can be found in common metals and in the interiors of white dwarf stars.

We'll look at a gas of fermions in the degenerate regime, where the density n exceeds the quantum density n q by a large factor, or when the Fermi energy exceeds the temperature by a large factor. We've seen that for such a gas, is positive, therefore we'll focus on the Fermi energy EF, which is near to its T=0 value.

The electron gas in metals and white dwarf stars is the most important degenerate Fermi gas. Another example is a neutron star with such a high density that the neutron gas is degenerate.

Q19) What is the Fermi function.

A19)

The Fermi-Dirac probability density function calculates the likelihood of a fermion in thermal equilibrium with a large reservoir occupying a certain energy level. Fermions are particles that have a half-integer spin (1/2, 3/2, 5/2, etc.). The Pauli exclusion principle asserts that only one fermion can occupy a state specified by its set of quantum numbers n,k,l, and s. This is a unique property of fermions. As a result, particles that obey the Pauli exclusion principle could likewise be classified as fermions. All of these particles have a half-integer spin as well.

Both electrons and holes have a spin of 1/2 and follow Pauli's exclusion principle. These particles will fill the available states in an energy band when they are added to it, just like water fills a bucket. The lowest-energy states are filled first, followed by the next higher-energy levels. The energy levels are all filled up to a maximum energy, which we call the Fermi level, at absolute zero temperature (T = 0 K). There are no states filled above the Fermi level. The transition between entirely filled and completely empty states is gradual rather than sudden at higher temperatures. This behaviour is described by the Fermi function, which is:

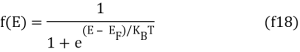
In the graph below, this function is plotted at ambient temperatures of 150 K (red curve), 300 K (blue curve), and 600 K. (black curve).

T = 150 K (red curve), 300 K (blue curve), and 600 K Fermi-Dirac distribution function (black curve).

For energies more than a few times kT below the Fermi energy, the Fermi function has a value of one, equals 1/2 if the energy equals the Fermi energy, and declines exponentially for energies a few times kT bigger than the Fermi energy. While the Fermi function equals a step function at T = 0 K, the transition at finite temperatures and higher temperatures is more gradual.

The section on distribution functions has a more extensive description of the Fermi function and other distribution functions.

Q20) What are the 3-D Density of states?

A20)

Solving the Schrödinger equation for the particles in the semiconductor yields the density of states in the semiconductor. Rather than using the actual and complex potential in the semiconductor, the simple particle-in-a-box model is usually used, in which the particle is assumed to be free to move within the material. For this and other more sophisticated models, the boundary conditions, which describe the fact that particles cannot leave the material, cause the density of states in k-space to stay constant. If the E-k relation is known, the density of states corresponding to it can be found. For a comprehensive derivation in one, two, and three dimensions, the reader should refer to the section on density of states.

The density of states in three dimensions for an electron that behaves as a free particle with effective mass, m*, is given by:

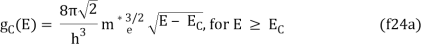
Ec is the conduction band's lowest point, below which the density of states is zero. For holes in the valence band, the density of states is given by:

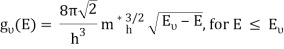
Unit - 3

Quantum Statistics

Q1) Explain Macrostates and microstates.

A1)

A microstate, for example, defines the position and momentum of each particle in a classical system of point particles. It determines the value of the wavefunction at every point in space in a quantum mechanical system. You must give the most thorough description you will ever care about to define what microstate the system is in.

You might be thinking if this is a reasonable assumption. What if there aren't any discrete microstates? A classical particle's position and momentum, for example, are continuous rather than discrete. At its most fundamental level, the question of whether the cosmos is discrete or continuous remains unanswered. Fortunately, this turns out not to matter very much. You can always turn a continuous variable into a discrete one by dividing it into very small bins. For the classical particle, we treat all positions between xx and x+δx and all momenta between pp and p+δp as a single microstate. As long as we choose δx and δp sufficiently small, the exact values turn out to have no effect on most of our results.

This is depicted in Figure, which depicts the space of possible microstates in one dimension for a single particle. The values of x and p define each microstate. This is known as phase space, and we'll be using it a lot. A 2dN dimensional phase space exists for a system of N particles in dddimensions. In this phase space, each point represents a microstate.

Each axis is segmented into very small intervals. A microstate is a volume defined by the intersection of one interval from each axis.

The number of microstates in ordinary systems is enormous, and they characterise the system in far more detail than humans generally care about. Consider the case of a gas-filled box. You have no means of knowing the exact position and momentum of every single gas molecule, and even if you could, you wouldn't care. Instead, you're usually just concerned with a few macroscopic variables: the system's total energy, the total number of gas molecules, the volume of space it occupies, and so on. These are things that can be measured and are useful in the real world.

The value of each macroscopic variable is used to define a macrostate. It's possible that a large number of microstates belong to the same macrostate. Let's say you want to calculate the total energy and volume of a box of gas. There are a huge variety of different configurations of individual gas molecules that sum up to that amount of energy and volume. You're quite sure the gas is in one of those states, but you're not sure which one.

Q2) Explain Fermions and Bosons statement.

A2)

Fermions

Any particle with an odd half-integer spin (such as 1/2, 3/2, and so on) is called a fermion. Fermions include quarks and leptons, as well as most composite particles like protons and neutrons.

The odd half-integer spin has the unintended consequence of obeying the Pauli Exclusion Principle, which means fermions cannot exist in the same state at the same time for reasons we don't fully comprehend.

Bosons

The particles with an integer spin are known as bosons (0, 1, 2...).

All force carrier particles, as well as composite particles containing an even number of fermion particles, are bosons (like mesons).

Depending on whether the total number of protons and neutrons in an atom is odd or even, the nucleus is a fermion or a boson. Physicists recently discovered that this has resulted in some odd behaviour in particular atoms under extraordinary settings, such as extremely cold helium.

Q3) What's The Difference Between A Fermion And A Boson?

A3)

In the entire Universe, there are only two types of fundamental particles: fermions and bosons. Every particle possesses an intrinsic quantity of angular momentum, often known as spin, in addition to the usual attributes such as mass and electric charge. Fermions are particles with spins in half-integer multiples (e.g., 1/2, 3/2, 5/2, etc.) while bosons are particles with spins in integer multiples (e.g., 0, 1, 2, etc.). In the entire known Universe, there are no other forms of particles, basic or composite. But why is this significant? The following is a question from an anonymous reader:

At first look, it may appear that classifying particles based on these characteristics is utterly arbitrary.

The Standard Model's known particles. This is a list of all the fundamental particles that have been discovered... [plus]

SIEGEL, E.

After all, isn't a particle just a particle? Surely there are more differences between quarks and leptons (which do not experience the strong force) than there are between fermions and bosons? Surely there's more to the difference between matter and antimatter than your particle's spin? And whether you're gigantic or massless should be a major concern, right? Especially when compared to something like angular momentum, right?

As it turns out, there are a number of little changes in spin that matter, but there are two major ones that impact far more than most people, including physicists, understand.

The photons, particles and antiparticles of the early Universe. It was filled with both bosons and... [+]

Q4) Write a short note on Andrew Deniszczyc.

A4)

You may also form composite particles out of fermions: a proton (which is a fermion) is made up of two up quarks and one down quark, whereas a neutron is made up of one up and two down quarks (also a fermion). Because of how spins function, if you bind an odd number of fermions together, your new (composite) particle will behave like a fermion, which is why protons and antiprotons exist, and why a neutron differs from an antineutron. However, particles made up of an even number of fermions, such as a quark-antiquark pair (known as a meson), act like a boson. The neutral pion (π0), for instance, is its own antiparticle.

The reason behind this is simple: each of those fermions is a spin ±1/2 particle. If you add two of them together, you can get something that's spin -1, 0, or +1, which is an integer (and hence a boson); if you add three, you can get -3/2, -1/2, +1/2, or +3/2, As a result, it's a fermion. As a result, particle/antiparticle differences are significant. However, there is a second distinction that is arguably much more significant.

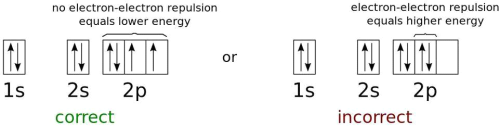
Fig. The electron energy levels of a neutral oxygen atom in the lowest feasible energy configuration.

Q5) What is foundation and adrignola of wikimedia commons.

A5)

Only fermions, not bosons, are excluded under the Pauli exclusion principle. This rule expressly asserts that no two fermions can occupy the same quantum state in any quantum system. Bosons, on the other hand, are unrestricted. When you add electrons to an atomic nucleus, the first electron will tend to inhabit the ground state, which is the lowest energy state possible. The spin state of that electron can be either +1/2 or -1/2 because it's a spin=1/2 particle. If you add another electron to that atom, it must have the opposite spin state in order to be in the ground state as well.  They can no longer fit in the ground state and must progress to the next energy level.

Within a hydrogen atom, the energy levels and electron wavefunctions that correspond to different states... [+]

Q6) Write a short note on Poorleno Of Wikimedia Commons And Jenny Mottar.

A6)

POORLENO OF WIKIMEDIA COMMONS:

That is why the periodic table is set up the way it is. This is why atoms have diverse properties, why they bond together in such complex ways, and why each element in the periodic table is distinct: each type of atom has a different electron configuration than the others. The physical and chemical properties of the elements, the vast variety of molecular configurations we have today, and the basic bonds that allow complex chemistry and life to exist are all due to the fact that no two fermions can occupy the same quantum state.

The way atoms join together to form compounds, such as organic compounds and biological activities,... [+]

JENNY MOTTAR

On the other side, you can put as many bosons in the same quantum state as you want! This enables the production of Bose-Einstein condensates, which are extremely rare bosonic states. You can put any number in there by cooling bosons sufficiently such that they fall into the lowest energy quantum state. At low enough temperatures, helium (which is made up of an even number of fermions and hence acts like a boson) becomes a superfluid as a result of Bose-Einstein condensation. Gases, molecules, quasi-particles, and even photons have all been condensed since that time. It's still a hot topic of study today.

Before (L), during (Middle), and after (R) the... [+] A Bose-Einstein condensate of rubidium atoms before (L), during (Middle), and after (R) the…

Q7) Introduce the Bose Einstein distribution function and Fermi –Dirac distribution function.

A7)

The probability density functions, also known as distribution functions, represent the likelihood that particles would occupy the available energy levels in a particular system. While the actual derivation belongs in a statistical thermodynamics course, understanding the underlying assumptions of such derivations, and hence the applicability of the results, is of importance.

The derivation begins with the premise that each potential particle distribution over the available energy levels has the same probability as any other potential distribution that can be separated from the first.

Furthermore, one considers the fact that both the total number of particles and the total energy of the system have a particular value.

Third, one must recognise that various particles behave differently. At any given energy level, only one Fermion can exist (as described by a unique set of quantum numbers including spin). There is no limit to the number of bosons that can occupy the same energy levels. Fermions and bosons have the same "appearance," that is, they are indistinguishable. It is possible to differentiate Maxwellian particles from one another.

Using the Lagrange method of indeterminate constants, the derivation then produces the most likely particle distribution. One of the Lagrange constants, the average energy per particle in the distribution, turns out to be a more important physical quantity than the total energy. The Fermi energy, or EF, is the name for this variable.

The fact that one is dealing with a high number of particles is an important assumption in the derivation. This assumption allows the Stirling approximation to be used to approximate the factorial terms.

The resulting distributions have several unusual properties that are difficult to explain. First and foremost, regardless of whether a specific energy level exists or not, a probability of occupancy can be calculated. Since the density of possible states defines where particles can be in the first place, it seems more reasonable that the distribution function is dependent on it.

The assumption that a given energy level is in thermal equilibrium with a large number of other particles causes the distribution function to be independent of the density of states. It is unnecessary to go into detail on the nature of these particles because their number is so large. The density of states' independence is advantageous since it gives a single distribution function for a wide range of systems.

The image below shows a plot of the three distribution functions, the Fermi-Dirac distribution, the Maxwell-Boltzmann distribution, and the Bose-Einstein distribution, with the Fermi energy set to zero.

The Fermi-Dirac (red curve), Bose-Einstein (green curve), and Maxwell-Boltzman (blue curve) distributions show occupancy probability versus energy.

For large energies, the three distribution functions are nearly equivalent (more than a few kT beyond the Fermi energy). For energies a few kT below the Fermi energy, the Fermi-Dirac distribution reaches a maximum of 1, whereas the Bose-Einstein distribution diverges at the Fermi energy and has no validity for energies below the Fermi energy.

Q8) State the Fermi-Dirac distribution function.

A8)

The Fermi-Dirac probability density function calculates the likelihood of a Fermion in thermal equilibrium with a large reservoir occupying a certain energy level. Fermions are particles that have a half-integer spin (1/2, 3/2, 5/2, etc.). The Pauli exclusion principle asserts that only one Fermion can occupy a state specified by its set of quantum numbers n,k,l, and s. This is a unique property of Fermions. As a result, Fermions could alternatively be defined as particles that follow the Pauli exclusion principle. All of these particles have a half-integer spin as well.

Both electrons and holes have a spin of 1/2 and follow Pauli's exclusion principle. These particles will fill the available states in an energy band when they are added to it, just like water fills a bucket. The lowest-energy states are filled first, followed by the next higher-energy levels. The energy levels are all filled up to a maximum energy, which we call the Fermi level, at absolute zero temperature (T = 0 K). There are no states filled above the Fermi level. The transition between entirely filled and completely empty states is gradual rather than sudden at higher temperatures. This behaviour is described by the Fermi function, which is:

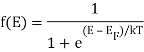
Q9) Define Bose- Einstein Condensation.

A9)

The exotic quantum phenomena of Bose-Einstein condensation was first detected in dilute atomic gases in 1995, and it is currently the focus of extensive theoretical and experimental research.

The cloverleaf magnetic trap at MIT is set up for evaporative cooling. Axial confinement is provided by the middle (curvature) coils, while radial confinement is provided by the outside coils (the "clover leaves" or gradient coils). Cigar-shaped clouds are formed as a result of the anisotropic potential. The most energetic atoms' spins are preferentially flipped by radio-frequency radiation from an antenna, while the remainder atoms rethermalize to a lower temperature. The radio-frequency is lowered to force cooling.

Satyendra Nath Bose, an Indian physicist, wrote Einstein a paper in 1924 in which he calculated the Planck rule for black-body radiation by treating photons as a vapour of identical particles. In the same year, Einstein extended Bose's theory to an ideal gas of identical atoms or molecules, in which the number of particles is conserved, and predicted that the particles would get trapped together in the system's lowest quantum state at sufficiently low temperatures. We now know that Bose-Einstein condensation (BEC) occurs only for “bosons” — particles having a total spin that is an integer multiple of h, the Planck constant divided by 2 pi.

This Bose condensate, as well as the condensation process itself, was predicted to exhibit a variety of odd features, and scientists have been attempting to create Bose-Einstein condensation in the laboratory for years. Finally, in 1995, researchers from the Massachusetts Institute of Technology (MIT) and JILA, a laboratory maintained by the National Institute of Standards and Technology and the University of Colorado in Boulder, Colorado, uncovered convincing evidence for Bose-Einstein condensation in dilute atomic gases.

Since then, the Boulder and MIT teams, as well as a team at Rice University in Houston, Texas, have refined the procedures for making and studying this unique quantum phenomena, and rapid progress has been made in understanding its dynamic and thermodynamic features. At MIT, we recently confirmed the fascinating property of Bose-condensed atoms being "laser-like" — that is, that the atoms' matter waves are coherent. We were able to observe coherence directly in these experiments, and we developed a crude "atom laser" that generates a beam of coherent atoms, similar to how an optical laser emits coherent photons. Simultaneously, theorists have addressed a number of fundamental difficulties and devised effective ways for simulating real-world systems.

Q10) Describe the Order reigns in the ground state as per Bose- Einstein Condensation.

A10)

The dynamical behaviour of a gas at room temperature is not affected by the fact that one atom cannot be distinguished from another. In accordance with the Heisenberg uncertainty principle, the position of an atom is smeared out over a distance given by the thermal de Broglie wavelength, lambdadB = (2 pi h-bar2 / kBmT)1/2, where kB is the Boltzmann constant, m is the atomic mass and T is the temperature of the gas. At room temperature the de Broglie wavelength is typically about ten thousand times smaller than the average spacing between the atoms. This means that the matter waves of the individual atoms are uncorrelated or “disordered”, and the gas can thus be described by classical Boltzmann statistics.

As the gas is cooled, however, the smearing increases, and eventually there is more than one atom in each cube of dimension lambdadB. The wavefunctions of adjacent atoms then “overlap”, causing the atoms to lose their identity, and the behaviour of the gas is now governed by quantum statistics.

Bose-Einstein statistics dramatically increase the chances of finding more than one atom in the same state, and we can think of the matter waves in a Bose gas as “oscillating in concert”. The result is Bose-Einstein condensation, a macroscopic occupation of the ground state of the gas. (In contrast, fermions – particles with a total spin of (n + ½)h, where n is an integer – cannot occupy the same quantum state.) Einstein described the process as condensation without interactions, making it an important paradigm of quantum statistical mechanics.

The density distribution of the condensate is represented by a single macroscopic wavefunction with a well defined amplitude and phase, just as for a classical field. Indeed, the transition from disordered to coherent matter waves can be compared to the change from incoherent to laser light.

Q11) Define the term Chilling the atoms.

A11)

Bose-Einstein condensation has been cited as an important phenomenon in many areas of physics, but until recently the only evidence for condensation came from studies of superfluid liquid helium and excitons in semiconductors. In the case of liquid helium, however, the strong interactions that exist in a liquid qualitatively alter the nature of the transition. For this reason a long-standing goal in atomic physics has been to achieve BEC in a dilute atomic gas. The challenge was to cool the gases to temperatures around or below one microkelvin, while preventing the atoms from condensing into a solid or a liquid.Efforts to Bose condense atoms began with hydrogen more than 15 years ago. In these experiments hydrogen atoms are first cooled in a dilution refrigerator, then trapped by a magnetic field and further cooled by evaporation (see below). This approach has come very close to observing BEC, but is limited by the recombination of individual atoms to form molecules and by the detection efficiency. In the 1980s laser-based techniques such as Doppler cooling, polarization-gradient cooling and magneto-optical trapping were developed to cool and trap atoms. These techniques profoundly changed the nature of atomic physics and provided a new route to ultracold temperatures that does not involve cryogenics. Atoms at sub-millikelvin temperatures are now routinely used in a variety of experiments. Alkali atoms are well suited to laser-based methods because their optical transitions can be excited by available lasers and because they have a favourable internal energy-level structure for cooling to low temperatures. However, the lowest temperature that these laser cooling techniques can reach is limited by the energy of a single photon. As a result, the “phase-space density” – the number of atoms within a volume lambdadB3 – is typically about a million times lower than is needed for BEC.

The successful route to BEC turned out to be a marriage of the cooling techniques developed for hydrogen and those for the alkalis: an alkali vapour is first laser cooled and then evaporatively cooled. In evaporative cooling, high-energy atoms are allowed to escape from the sample so that the average energy of the remaining atoms is reduced. Elastic collisions redistribute the energy among the atoms such that the velocity distribution reassumes a Maxwell-Boltzmann form, but at a lower temperature. This is the same evaporation process that happens when tea cools, but the extra trick for trapped atoms is that the threshold energy can be gradually lowered. This allows the atomic sample to be cooled by many orders of magnitude, with the only drawback being that the number of trapped atoms is reduced.

The challenge in combining these two cooling schemes for alkalis was a question of atomic density. Optical methods work best at low densities, where the laser light is not completely absorbed by the sample. Evaporation, on the other hand, requires high atomic densities to ensure rapid rethermalization and cooling. This changed the emphasis for optical methods: while they had previously been used to produce low temperatures and high phase-space density simultaneously, they now needed to produce high elastic collision rates. Furthermore, this had to be achieved in an ultrahigh vacuum chamber to prolong the lifetime of the trapped gas. Thus no new concept was needed to achieve BEC, but rather it was an experimental challenge to improve and optimise existing techniques. These developments were pursued mainly at MIT and Boulder from the early 1990s.

Q12) Define the Improved techniques in magnetic trapping.

A12)

For evaporative cooling to work, the atoms must be thermally isolated from their surroundings. This must be done with electromagnetic fields, since at ultracold temperatures atoms stick to all surfaces. The best method for alkalis is magnetic confinement, which takes advantage of the magnetic moment of alkali atoms. After the atoms are trapped and cooled with lasers, all light is extinguished and a potential is built up around the atoms with an inhomogeneous magnetic field. This confines the atoms to a small region of space.

Atoms can only be cooled by evaporation if the time needed for rethermalization is much shorter than the lifetime of an atom in the trap. This requires a trap with tight confinement, since this allows high densities and hence fast rethermalization times. For this reason, the first experiments that observed BEC used so-called linear quadrupole traps, which have the steepest possible magnetic fields. At MIT, dispersive light scattering (phase-contrast imaging) was used to observe the development of a Bose condensate in a direct and non-destructive way. The intensity of dispersed light is plotted as a function of trap position, which is proportional to the atom column density along the line of sight. The cloud has been cooled to just above the BEC transition temperature in the figure on the left, and the atom distribution is practically classical. A strong peak of atoms appears at the trap centre (middle) as the temperature is decreased across the phase transition, and further cooling increases the condensate fraction to nearly 100%. (right).

These approaches do create great densities and rapid evaporation, but they have one fundamental flaw: the magnetic field at the centre is zero, causing an atom to become "disoriented" and lose its magnetic moment's alignment. These "spin flips" result in a calamitous loss of atoms from the trap since a magnetic field can only confine atoms with magnetic moments that are antiparallel to the field. Both the Boulder and MIT teams devised solutions to the challenge. A rotating magnetic field was created by the Boulder group to keep the atoms away from the "hole," while we "plugged" the hole using the repulsive force of a focused laser beam.

Both of these methods were successful, yet they both had significant flaws. We discovered BEC in an unique "cloverleaf" magnetic trap that overcome these restrictions in March 1996. This trap is a modification of the Ioffe-Pritchard trap, which was first proposed in 1983 and contains a non-zero magnetic field at its centre to prevent atom loss. The confinement is tight in two directions but weak in the third, resulting in cigar-shaped trapped clouds rather than spherical trapped clouds. The trap's unique feature is the coils' "cloverleaf" winding arrangement, which provides good optical access to the sample for laser cooling and trapping, as well as probing the condensate (see figure 1). The trap's design has proven to be dependable and versatile, and it was used to gather the majority of the experimental results shown here. Given the amount of effort that has gone into trap design in recent years, it's remarkable that the best setup has been around for almost 13 years.

Using electron spin resonance, evaporation can be easily accomplished in a magnetic trap. Applying a radio-frequency field in resonance with the energy difference between the spin-up and spin-down states flips the magnetic moments of trapped atoms. The field's frequency is set such that it only impacts the atoms at the cloud's edge, which have the most energy in a harmonic oscillator potential. The magnetic forces become anti-trapping and the atoms are freed from the trap when the moments of these atoms are inverted. Because the cloud cools and shrinks towards the trap's centre, the frequency of the radio-frequency field must be decreased to keep evaporation at the cloud's perimeter.

In our trials, sodium atoms are ejected from an oven at 600 K (800 m s-1) and a density of around 1014 cm-3. The atoms are initially slowed to a speed of roughly 30 m s-1 over a distance of 0.5 m using a laser beam. Around 1010 atoms can be trapped in a magneto-optical trap at this speed. The temperature of the gas is reduced to roughly 100 K using laser cooling and trapping techniques, which is cold enough for the atoms to be trapped with magnetic fields. In about 20 seconds, evaporation cools the gas to about 2 K, the temperature at which a condensate develops.

Q13) What is meant by Observing condensation.

A13)

Condensates trapped in the trap are very tiny and optically thick, making them difficult to see. By turning off the trap and letting the atoms to expand ballistically, the first observations of BEC were made. After that, a laser beam in resonance with an atomic transition was flashed on, and the subsequent light absorption generated a "shadow" that was captured by a camera. This picture of atomic locations records the velocity distribution of the atoms since they were released from the trap. Because the atoms in the condensate are in the lowest energy state, they expand very little, and the dramatic mark of Bose condensation was thus the abrupt development of a prominent peak of atoms in the image's centre.

Because the atoms are freed from the trap, absorption imaging is fundamentally destructive. Furthermore, the atoms are heated by the absorbed photons. In early 1996, we used "dark-ground" imaging, a technique that depends on dispersion rather than absorption, to examine a Bose condensate non-destructively.

A complicated index of refraction can be used to characterise both dispersion and absorption. The absorption of photons from the probe beam is described by the imaginary part of the index, which is followed by inelastic scattering of light over high angles. Coherent elastic scattering over small angles corresponds to the real part. The phase of the light is altered by dispersive scattering, and because the light is only slightly deflected, the technique is nearly non-perturbative. The crucial point is that if the probing laser is detuned far enough away from any atomic resonances, dispersive scattering dominates absorption, and the condensate resembles a piece of shaped glass, or a lens.

The phase shift induced by the atoms must be converted into an intensity variation in order to “see” the condensate using dispersive scattering. This is a well-known optical problem that can be solved by spatial filtering. Opaque objects (“dark-ground imaging”) or phase-shifters (“phase-contrast imaging”) are used to alter the signal in the Fourier plane.

Because dispersive imaging is non-destructive, many photographs of the same condensate can be acquired. Figure 2 shows phase-contrast imaging of the development of a condensate. Such real-time pictures will be essential in researching a condensate's dynamical behaviour.

Q14) What is Realization of a basic atom laser.

A14)

The possibility of producing a coherent beam of atoms, which could be collimated to travel large distances or brought to a tiny focus like an optical laser, has sparked the imagination of atomic physicists. Such an atom laser could have a major impact on the fields of atom optics, atom lithography and precision measurements.

A Bose-Einstein condensate is a sample of coherent atomic matter and is thus a good starting point for an atom laser. The process of condensing atoms into the ground state of a magnetic trap is analogous to stimulated emission into a single mode of an optical laser and one can think of the trap as a resonator with “magnetic mirrors”. An important feature of a laser is an output coupler to extract a fraction of the coherent field in a controlled way, and at MIT we recently demonstrated such a device for a trapped Bose gas.

The tiny, straight striations have a period of 15 m and are fringes caused by matter-wave interference. The ballistic expansion from a harmonic double-well potential is responsible for the significantly bigger modulations in the cloud structure.

Because a magnetic trap can only confine atoms with magnetic moments that are antiparallel to the magnetic field, we changed the “reflectivity” of the magnetic mirrors by tilting the atoms' magnetic moments using a short radio-frequency pulse. The atoms were removed in this manner, accelerated under gravity, and absorption imaging was used to examine them. The extracted fraction may be changed between 0% and 100% by altering the amplitude of the radio-frequency field (see Physics World 1996 October p18).

The coherence of a laser's output, or the presence of a macroscopic wave, is an important aspect. Coherence has been utilised as a defining condition for BEC in theoretical treatments. However, none of the measurements detailed thus far have shown long-range order. Although collective measurements match with Schrödinger equation solutions at zero temperature, identical frequencies have been anticipated for a classical gas in the hydrodynamic regime.

Examining the impacts of the phase of the condensate wavefunction is one way to explore coherence. The Josephson effect has been used to see this phase in superconductors, and the motion of quantized vortices in liquid helium has been used to infer it. Because phase is a complex number, it can only be recognised as an interference effect between two different wavefunctions, similar to how interference between two independent laser beams may be detected. Theoretical work on coherence and the interference features of confined Bose gases has recently gotten a lot of interest. The theoretical issues that lie beneath are of great interest and concern. For example, can spontaneous symmetry breaking (an important topic in physics) apply in systems with few atoms, and what impact do particle-particle interactions have on the phase of the condensate.

We recently witnessed high-contrast interference of two separate Bose condensates at MIT, demonstrating that a condensate has a well-defined phase. By concentrating a sheet of light into the cloverleaf trap and repelling atoms from the centre, we created a double-well trapping potential. Evaporation resulted in the formation of two distinct condensates. These were left to free-fall and expand ballistically under gravity.

The clouds overlapped horizontally after lowering 1 cm, and absorption revealed the interference pattern (figure 6). The fringes have a period of 15 p.m., which matches the respective de Broglie wavelengths of the overlapping clouds. When the imaging system's resolving power is taken into account, the intensity difference between the light and dark fringes indicate that the atomic interference modulation was between 50% and 100%. Figure 6 has the unique feature of being a real-time snapshot showing interference. The wavefront of a single particle is separated and then recombined in classic experiments to demonstrate the wave aspect of matter, and this is repeated numerous times to build up an interference pattern.

Q15) How to see Planck's radiation law as a consequence of Bose Einstein statistics?

A15)

Planck's law is the result of the following factors.

1) The mode density per unit volume in a cavity is 8πυ2/c3.

2) Within each mode, assume Boltzmann statistics i.e the probability of having an energy E is given by p(E) ∝ e-E/kT

3) Ask that the energies E be discretized as nhν instead of continuous. Essentially, the difference between doing 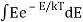 and the sum 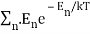, where  gives Planck's law.

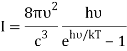
So far, it's a nice trick to go to the discrete sum but that's all that was done. There is no sense in which the particles are indistinguishable etc.

What is the correct modern way of seeing this result? I assume the starting point is that we have an ideal gas of photons inside a blackbody cavity and they follow statistics that yield 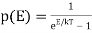 but how exactly does one go from there to Planck's law?

As you mentioned, we use a cavity as a model for blackbody radiation, for which you have already determined the mode density.

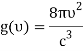
The photons' energies are discretized and have the formula E=nhv, where nn is an integer. The grand-canonical partition function for bosons with vanishing chemical potential will now be written down. Because photons interact with the cavity's walls, the number of photons isn't constant, it's taken to be zero. For a given frequency 0 the partition function is The energies that photons can have are discretized and have the formula E=nh, where nn is a positive integer. The grand-canonical partition function for bosons with vanishing chemical potential will now be written down. Because photons interact with the cavity's walls, the number of photons isn't constant, it's taken to be zero. For a given frequency 0 the partition function is

The total partition function can then be obtained by multiplying all of the frequency partition functions together.

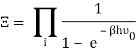
Taking the logarithm of ΞΞ will transform the product in a sum

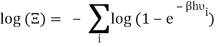
Which can be modified in an integral if the difference in frequency between two consecutive frequencies becomes minuscule. We can delegate this task to the density of modes g(v) instead of counting the number of photons per frequency:

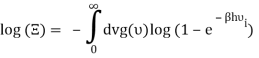
You can now calculate the energy associated using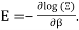 

So

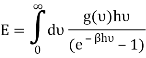
And from the relation 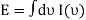  you find that

Q16) Write Bose deviation from Planck’s law.

A16)

According to Max Planck,19–21 a blackbody is a collection of numbers of oscillators. An oscillator emits or absorbs energy proportional to its oscillation frequency. Thus, emission or absorption of energy of a blackbody is discrete rather continuous which is termed as quantization of energy. This concept of quantization of electromagnetic radiation is used to explain the energy density distribution nature of a blackbody.

On the other hand, Louis de Broggle proposed that every moving object has a wave-particle dual character.12 According to the de Broggle, wavelength (λ) of a particle having momentum p, is hphp, where h is the Planck’s constant. Since oscillators are in motion and have momentum, they should have de Broggle wavelength.

Following Planck’s postulate,22 let us consider that the number of identical resonators per unit volume of a blackbody, having oscillation frequency ν, is N at the equilibrium temperature (T). If U is the vibrational energy of a resonator, the total energy per unit volume is NU. It is known that the rate of change of vibrational entropy, S, with respect to the change of vibrational energy, U, at a temperature T is –

If Ni number of particles occupy the ith vibrational state, the total energy of these particles are

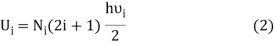
For frequency vi, the number of modes per unit volume is 82ic38i2c3. In this case, the total energy per unit volume for this frequency is calculated using the equipartition principle (classical technique).

Comparing Equation (2) and (3) we get an expression for the number of particles at ith vibrational state which is

Where v0 is the ground state vibrational energy's frequency. Equation can be used to compute a system's total internal energy (U) (4). The total energy per unit volume (U) of a system is equal to the number of particles per unit volume (N).

From Equation (5) we get

Or,

DU = BkdT                                                                                                              (7)

Where,

Putting the value of dU in Equation (1) we get

DS = Bkd (ln T)                                                                       (9)

On the integration of Equation (9), we get

S = Bkln T                                                                                  (10)

Because, for an ideal system, entropy is zero at 0K according to the third law of thermodynamics. It is also known that the thermal entropy is zero at the Bose-Einstein Condensate temperature.23,24

Following the Planck’s derivation22 of the entropy of an oscillator, we get

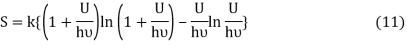
Where ν is the frequency of the oscillator. Equation (11) may be rearranged as

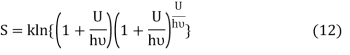
Comparing equation (10) and equation (12) we get

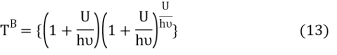
Equation (13) is also valid for ν0. If T0K is the Bose-Einstein condensate temperature of the system, then at T0K temperature all the oscillators should exist in the ground vibrational state. Thus, from Equation (13) we get

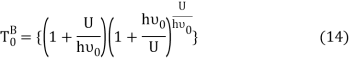
From equation (5) we get

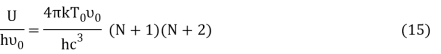
Let,

Where,

Putting this value of Uhν0Uhν0 in equation (14) we get the Bose-Einstein condensate temperature of the system of interest in terms of Z and B, which is

It is impossible to find the value of T0 unless Z and B are known. But, we can study the variation of T0 with the changes of Z and B.

Q17) Effect of temperature on Fermi –Dirac distribution function.

A17)

The electrons have little energy and hence inhabit lower energy states at T = 0 K. The Fermi-level is the highest energy state among these inhabited levels. As a result, electrons do not occupy any energy levels above the Fermi level. As a result, as indicated by the black curve in Figure 2, we get a step function that defines the Fermi-Dirac distribution function.

However, when the temperature rises, the electrons gather more and more energy, eventually reaching the conduction band. As a result, at higher temperatures, it is difficult to discriminate between the occupied and unoccupied states, as seen by the blue and red curves in Figure 2.

The free electrons in a solid crystal have different energies. According to quantum theory, free electrons continually occupy distinct energy levels at absolute zero temperature, with no gaps between filled states. Dropping the free electrons of a metal one by one into the potential well demonstrates this. The first electron to be dropped would occupy the lowest accessible energy level, say E0, and the following electron would do the same. The following energy level would be occupied by the third electron. Because of Pauli's exclusion principle, the third electron dropped would occupy the energy level E1 (>E0), and so on. If there are N (even) electrons in the metal, they will be dispersed in the first N/2 energy levels, with the higher energy levels being completely empty.

Distribution of electrons in various energy levels at 0 K.

The highest filled level, which separates the filled and empty levels at 0 K is known as the Fermi level and the energy corresponding to this level is called Fermi energy (EF). Fermi energy can also be defined as the highest energy possessed by an electron in the material at 0 K. At 0 K, the Fermi energy EF is represented as EF0. As the temperature of the metal is increased from 0 K to TK, then those electrons which are present up to a depth ofKBT from Fermi energy may take thermal energies equal to KBT and occupy higher energy levels, whereas the electrons present in the lower energy levels i.e., below KBT from Fermi level, will not take thermal energies because they will not find vacant electron states.

The probability that a particular quantum state at energy E is filled with an electron is given by Fermi-Dirac distribution function f(E), given by:

A graph has been plotted between f(E) and E, at different temperatures 0 K, T1 K, T2 K, T3 K.

Analytical Treatment At 0 K: Substitute T = 0 K in the Fermi-Dirac distribution, we have

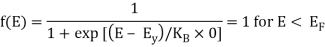
= 0 for E > EF

The curve has step-like character with f(E) = 1 for energies below EF0 and f(E) = 0 for energies above EF0. This represents that all the energy states below EF0 are filled with electrons and all those above it are empty.

At T > 0 K

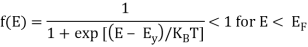
> 0 for E > EF

= ½ for E = EF

As the temperature is raised from absolute zero to T1K, the distribution curve begins to departs from step-like function and tails off smoothly to zero. Again with a further increase in temperature to T2K and to T3K, the departure and tailing of the curves increases. This indicates that more and more electrons may occupy higher energy states with an increase of temperature and as a consequence the number of vacancies below the Fermi level increases in the same proportion. At non-zero temperatures, all these curves pass through a point whose f(E) =1/2, at E = EF . So EF lies half way between the filled and empty states.

Q18) Define Degenerate Fermi gas.

A18)

In physics, a degenerate gas is a particular configuration of a gas made up of subatomic particles with half-integral intrinsic angular momentum that is frequently obtained at high densities (spin). Fermions are particles whose microscopic behaviour is governed by a set of quantum mechanical principles known as Fermi-Dirac statistics (q.v.). These principles specify, for example, that any quantum-mechanical state of a system can only have one fermion. Because the lower-energy states have all been filled, the extra fermions are forced to inhabit states of higher and higher energy as particle density rises. The pressure of the fermion gas rises as the higher-energy states gradually fill in, a phenomenon known as degeneracy pressure. A fully degenerate, or zero-temperature, fermion gas is one in which all of the energy levels below a certain value (named Fermi energy) are filled. All fermions, including electrons, protons, neutrons, and neutrinos, follow Fermi-Dirac statistics. Degenerate electron gas can be found in common metals and in the interiors of white dwarf stars.

We'll look at a gas of fermions in the degenerate regime, where the density n exceeds the quantum density n q by a large factor, or when the Fermi energy exceeds the temperature by a large factor. We've seen that for such a gas, is positive, therefore we'll focus on the Fermi energy EF, which is near to its T=0 value.

The electron gas in metals and white dwarf stars is the most important degenerate Fermi gas. Another example is a neutron star with such a high density that the neutron gas is degenerate.

Q19) What is the Fermi function.

A19)

The Fermi-Dirac probability density function calculates the likelihood of a fermion in thermal equilibrium with a large reservoir occupying a certain energy level. Fermions are particles that have a half-integer spin (1/2, 3/2, 5/2, etc.). The Pauli exclusion principle asserts that only one fermion can occupy a state specified by its set of quantum numbers n,k,l, and s. This is a unique property of fermions. As a result, particles that obey the Pauli exclusion principle could likewise be classified as fermions. All of these particles have a half-integer spin as well.

Both electrons and holes have a spin of 1/2 and follow Pauli's exclusion principle. These particles will fill the available states in an energy band when they are added to it, just like water fills a bucket. The lowest-energy states are filled first, followed by the next higher-energy levels. The energy levels are all filled up to a maximum energy, which we call the Fermi level, at absolute zero temperature (T = 0 K). There are no states filled above the Fermi level. The transition between entirely filled and completely empty states is gradual rather than sudden at higher temperatures. This behaviour is described by the Fermi function, which is:

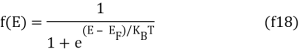
In the graph below, this function is plotted at ambient temperatures of 150 K (red curve), 300 K (blue curve), and 600 K. (black curve).

T = 150 K (red curve), 300 K (blue curve), and 600 K Fermi-Dirac distribution function (black curve).

For energies more than a few times kT below the Fermi energy, the Fermi function has a value of one, equals 1/2 if the energy equals the Fermi energy, and declines exponentially for energies a few times kT bigger than the Fermi energy. While the Fermi function equals a step function at T = 0 K, the transition at finite temperatures and higher temperatures is more gradual.

The section on distribution functions has a more extensive description of the Fermi function and other distribution functions.

Q20) What are the 3-D Density of states?

A20)

Solving the Schrödinger equation for the particles in the semiconductor yields the density of states in the semiconductor. Rather than using the actual and complex potential in the semiconductor, the simple particle-in-a-box model is usually used, in which the particle is assumed to be free to move within the material. For this and other more sophisticated models, the boundary conditions, which describe the fact that particles cannot leave the material, cause the density of states in k-space to stay constant. If the E-k relation is known, the density of states corresponding to it can be found. For a comprehensive derivation in one, two, and three dimensions, the reader should refer to the section on density of states.

The density of states in three dimensions for an electron that behaves as a free particle with effective mass, m*, is given by:

Ec is the conduction band's lowest point, below which the density of states is zero. For holes in the valence band, the density of states is given by: