Unit - 4

Radiation

Q1) What is black body radiation? Explain laws used to describe the properties of blackbody radiation?

A1)

"Blackbody radiation" or "cavity radiation" refers to an object or system that absorbs all incident radiation and re-radiates energy that is unique to this radiating system and is unaffected by the type of radiation it receives. Standing wave or resonant modes of the radiating cavity are thought to be the source of the radiated energy.

1. Planck's Law of Blackbody Radiation, which is a formula for calculating the spectral energy density of emission at each wavelength (E) for a given absolute temperature (T).

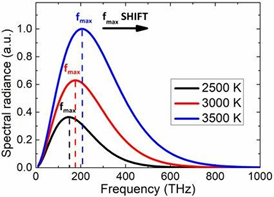
1. Wien's Displacement Law, according to which the frequency of the emission peak (fmax) increases linearly with absolute temperature (T). In contrast, as the body's temperature rises, the wavelength at the emission peak drops.

fmax ∝ T

E ∝ T4

As the temperature of the blackbody rises, the intensity (or flux) at all wavelengths rises as well.

As the temperature rises, the total energy radiated (the area under the curve) increases rapidly (Stefan–Boltzmann Law).

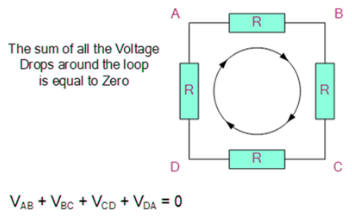
Q2) What do Kirchhoff’s laws state? Explain first and second law ?

A2)

Kirchhoff's First Law and Kirchhoff's Junction Rule are two names for Kirchhoff's Current Law. In a circuit, the amount of currents in a junction equals the sum of currents outside the junction, according to the Junction rule.

Kirchhoff's Second Law and Kirchhoff's Loop Rule are two names for Kirchhoff's Voltage Law. The total of the voltages around a closed loop is null, according to the loop rule

Kirchhoff’s First Law

The total current entering a junction or a node is equal to the charge exiting the node, according to Kirchhoff's Current Law, because no charge is lost.

To put it another way, the algebraic sum of all currents entering and exiting the node must be zero. Conservation of charge is the name given to this characteristic of Kirchhoff law.I(exit) + I(enter) = 0.

Kirchhoff’s Second Law

The voltage around a loop equals the sum of all voltage drops in the same loop for any closed network and also equals zero, according to Kirchhoff's Voltage Law.

To put it another way, the algebraic total of all the voltages in the loop must equal zero, and this property of Kirchhoff's law is known as energy conservation

Q3) What is Stefan Boltzmann Law? Derive Stefan Boltzmann Law Equation?

A3)

The amount of radiation emitted per unit time from an area A of a black body at absolute temperature T is exactly proportional to the fourth power of the temperature, according to Stefan Boltzmann's law.

u/A = σ T4 .. . . . (1)

Where σ is Stefan’s constant = 5.67 × 10-8 W/m2 k4

“Total energy emitted/radiated per unit surface” is a term used to describe how much energy is emitted or radiated per The temperature of a blackbody is proportional to the amount of power it emits per unit area, according to the Stefan Boltzmann Law. The area of a blackbody over all wavelengths per unit time is precisely proportional to the fourth power of the blackbody's thermodynamic temperature, according to this law.

Integrating Plank's radiation formula yields the total power radiated per unit area over all wavelengths of a dark body. As a function of wavelength, the radiated power per unit area is:

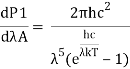
Where,

• P stands for radiated power.
• A is the blackbody's surface area, and is the wavelength of emitted radiation.
• Planck's constant is h.
• The speed of light is denoted by c.
• Boltzmann's constant is k.
• T stands for temperature.

When the Stefan Boltzmann equation is simplified, we get:

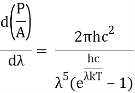
On integrating both sides in terms of and applying the restrictions that we obtain;

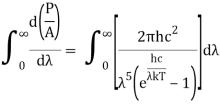
After removing the constants, the integrated power is:

Analytically, this can be solved by substituting:

x =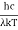

Therefore, dx = -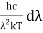

⟹ h =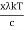

⟹ c =

⟹ d =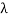

As a result of substituting them in equation (1)

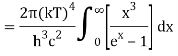
The following equation is equivalent to the conventional form of integral:

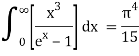
As a result of replacing the above result, we obtain

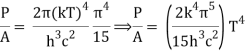
We get, when we simplify it even more,

⇒ P/A = σ T4

As a result, we arrive at a mathematical representation of Stephen Boltzmann's law:

⇒ε = σT4

Where,

ε = P/A

The behaviour of gases at low temperatures could be effectively expressed using this quantum mechanical result.

Q4) Explain Wein’s  Displacement Law? Explain the term used in formula of wein displacement?

A4)

Wien's displacement law describes one of the relationships between a black body's emission spectrum and temperature. It states that the lower the wavelength, the higher the temperature.λmax where the radiation curve achieves its pinnacle Photons with higher energy are associated with shorter wavelengths. To put it another way,λmax  Temperature and (peak wavelength) are inversely proportional

Formula:

The equation describing Wien's law is very simple:

λmax = b / T,

Where:

• λmax is the aforementioned peak wavelength of light
• T is an absolute temperature of a black body

b = 2.8977719 mm*K is the Wien's displacement

Q5) How to estimate the temperature of the Sun's surface?

A5)

We can acquire a good estimate by using the Wien's displacement method.law to the results. Let's try to calculate the temperature of the Sun's surface:

1. Find the peak wavelength of a solar spectrum. It's approximately λmax = 501.7 nm (or 5.017 * 10⁻⁷ m in the scientific notation).
2. Transform the Wien's law formula to obtain the temperature: T = b / λmax = 2.8977719 mm * K / 501.7 nm = 5776 K.

The Wien's law is universal and can be a fairly good approximation for real objects, despite the fact that the black body is only an idealised model.

Q6) Derive Wien’s Displacement Law from Planck’s Law?

A6)

The blackbody radiation curve at different temperatures peaks at a wavelength that is inversely proportional to the temperature, according to Wien's displacement law. The Planck radiation law, which specifies the spectrum brightness of black body radiation as a function of wavelength at any given temperature, causes that peak to shift.

Planck's law is used to derive Wien's displacement law. Follow these steps:

ρ(v, T) =                                                                      (1)

To get the peak wavelength, we must evaluate the derivative of Equation 1 with respect to v and set it to zero.

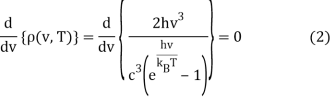
This can be solved via the quotient rule or product rule for differentiation. If you choose the latter, you'll need to rewrite Equation 2 as a product:

The application of the product rule (and power rule and chain rule)

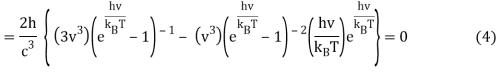
As a result, when this expression is zero,

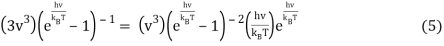
Or when simplified

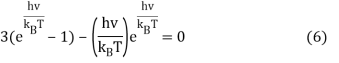
We can do a substitution u=hνkBT and Equation 6 becomes

3(eu – 1) – ueu = 0                                                                                (7)

Using Lambert's W-functions to find the solutions to this equation yields numerical data in

u = 3 + W(-3e-3 ) ≈ 2.8214                                               (8)

So unsubstituting the u variable

u = 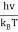≈ 2.8214                                               (9)

Or

v ≈ 2.8214 kBT/h                                                                            (10)

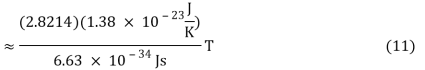
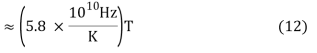
Q7) Explain Planck’s Law of Black body Radiation?

A7)

The spectral-energy distribution of radiation emitted by a blackbody (a hypothetical body that completely absorbs all radiant energy falling upon it, reaches some equilibrium temperature, and then reemits that energy as quickly as it absorbs it). Planck hypothesised that the sources of radiation are oscillating atoms, and that each oscillator's vibrational energy can take any of a number of discrete values, but never any value in between. Planck also assumed that when an oscillator switches from one state of energy E1 to another of lower energy E2, the discrete amount of energy E1 E2, or quantum of radiation, is equal to the product of the frequency of the radiation, symbolised by the Greek letter v, and a constant h, now known as Planck's constant, which he calculated from blackbody radiation data.i.e., E1 − E2 = hν.

Planck’s law for the energy Eλ radiated per unit volume by a cavity of a blackbody in the wavelength interval λ to λ + Δλ (Δλ denotes an increment of wavelength) can be written in terms of Planck’s constant (h), the speed of light (c), the Boltzmann constant (k), and the absolute temperature (T):

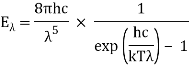
The emitted radiation's wavelength is inversely proportional to its frequency, orλ = c/ν. The value of Planck’s constant is defined as 6.62607015 × 10−34 joule∙second.

The majority of the radiation emitted by a blackbody at temperatures up to several hundred degrees is in the infrared region of the electromagnetic spectrum. At higher temperatures, the total radiated energy rises, and the intensity peak of the emitted spectrum moves to shorter wavelengths, resulting in visible light being released in greater amounts.

Q8) Explain Rayleigh Jeans Law and its derivation?

A8)

The Rayleigh-Jeans Radiation Law was an attempt to determine the functional form of thermal radiation spectra that was useful but not entirely successful. According to The Rayleigh-Jeans Radiation, the energy density uv per unit frequency interval at a frequency is

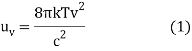
Where k is Boltzmann's constant, T is the radiating body's absolute temperature, and c is the speed of light in vacuum.

Consider a cube with an edge length L that reflects and re-reflects radiation off its walls. Standing waves form when an integral number of half-wave cycles fits inside a cube interval for radiation of a wavelength. This is required for radiation parallel to a cube's edge.

Where m is an integer or, equivalently

λ = 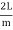                                                                                     (3)

Consider an L-edged cube that reflects and re-reflects radiation off its walls. When an integral number of half-wave cycles fits inside a cube interval for wavelength radiation, standing waves arise. Radiation parallel to a cube's edge requires this.

Working with the quantity q, often known as the wavenumber, which is defined as

And hence

In terms of the cube's relationship,

And hence

The radian frequency (=2v) is another useful word. It follows from this that q=ω/c.

The requirement for a standing wave in the cube is that mX, mY, and mZ signify the integers for the three different directions in the cube.

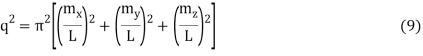
Which reduces to

The goal now is to determine the number of nonnegative (mX, mY, mZ) combinations that fit between a sphere of radius R and one of radius R+dR. To begin, determine the number of combinations that do not violate the non-negativity criteria.

The volume of a spherical shell with inner radius R and outer radius R+dR can be calculated using the formula

DV = 4π R2dR                                                           (11)

If

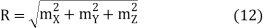
Then

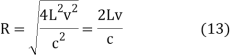
And hence

This means that

DV = 4π(2Lv/c)2(2L/c)dv = 32π(L3v2/c3)dv                                                             (15)

The non-negativity requirement for the combinations (mX, mY, and mZ) must now be considered. The nonnegative options in the two-dimensional example are roughly those in one circle quadrant. The matter of the combinations on the nonnegative quadrant's bounds gives rise to the approximation. Nonnegative combinations account for about one octant of the total in the three-dimensional example.Thus the number dN for the nonnegative combinations of (mX, mY, mZ) in this volume is equal to (1/8)dV and hence

DN = 4πv2dv                                                                                          (16)

Per degree of freedom, the average kinetic energy is½kT, The Boltzmann constant is k. Because kinetic and potential energy are identical in harmonic oscillators, the average energy per degree of freedom is kT. This means that the average radiation energy E per unit frequency can be calculated as follows:

Where the average energy density, uv, is calculated as follows:

The prior merely took into account one polarisation orientation for the radiation. If the two polarisation orientations are considered, a factor of 2 must be added to the above calculation; i.e.,

As the frequency approaches 0, the Raleigh-Jeans Law of Radiation holds empirically.

Q9) What is saha’s Equation?

A9)

The mathematical relationship between the measured spectra of stars and their temperatures is known as the Saha equation. It describes how the ionisation state of any given element in a star changes as temperature and pressure change. Because each atom or ion can absorb or emit radiation of a certain range of wavelengths, the spectrum of a star is directly related to the relative amount of atoms and ions it contains.

The Saha formula is

Where Ni + 1 and Ni are the number of atoms in the (i + 1)th and ith ionization states, respectively; Ui + 1 and Ui describe how energy is partitioned among the (i + 1)th and ith ionization states; Ei + 1 and Ei are the energies of the ionization states; Ne is the number of electrons; and T is the temperature.

Q10) Explain Wein’s distribution law?

A10)

Wien discovered a relationship between the monochromatic emittance of an ideal blackbody and its temperature based only on thermodynamic logic.

Where e is a blackbody's monochromatic emittance (emissive power) at wavelength and absolute temperature T, and f(T) is a function that cannot be derived only on thermodynamic grounds. A)

The energy of a black body in the wavelength interval, according to Wien, is given by

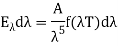
Wien discovered that the form of the function depends on the Maxwell-Boltzmann distribution law for the speed of atoms (or molecules) in a gas.  was

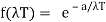
And so

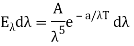
Where A and a were constants to be determined.

If we want to represent this in terms of frequency rather than wavelength, we must remember that, according to the wave equation., c = v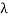 and so 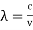. But, we also need to rewrite  d 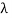in terms of dv and to do this we write

v = c/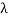→ d = -c/ v2 dv

The minus sign can be ignored because it just indicates that as the frequency increases, the wavelength decreases, and therefore substituting for 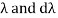 we can write that the energy in the frequency interval dv is given by

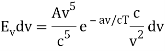
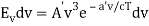
Where A’ and a’ are also just constants to be determined.

Q11) Explain First Law of Thermodynamics?

A11)

The first law of thermodynamics can be applied at this moment since the photon gas is equivalent to a classical ideal gas. It is written in differential form as follows (where S is the entropy):

DU = T . DS – p . DV                      First law of thermodynamics                         (14)

At constant temperature, dividing this equation by dV yields the following relationship:

Without going into the details of how the so-called Maxwell thermodynamic connections are derived, they reveal another crucial relationship at this point: At constant temperature, a change in entropy and a change in volume have the same connection as a change in pressure and a change in temperature. This is stated mathematically as follows:

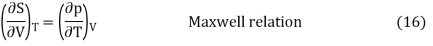
Q12) If R1 = 2Ω, R2 = 4Ω, R3 = 6Ω, determine the electric current that flows in the circuit below.

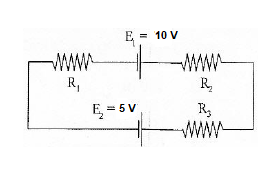
A12)

There is a potential drop when current travels over the resistor. As a result, V = IR has a negative sign. Because of the charging of energy at the emf source, the source of emf (E) signs positive as the current moves from low to high. Similarly, if the current changes from high to low voltage (+ to -), the source of emf (E) signs negative due to the emf source's energy being depleted.

The current flows in the same direction as the clockwise rotation.

– IR1 + E1 – IR2 – IR3 – E2 = 0

Substituting the values in the equation, we get

–2I + 10 – 4I – 6I – 5 = 0

-12I + 5 = 0

I = -5/-12

I = 0.416

The circuit has a current of 0.416 A flowing through it. The electric current is signed positive, which indicates that it rotates in the same direction as the clock. If the electric current is negative, it will flow in an anti-clockwise direction.