UNIT 3

Digital Fundamentals

1.    Explain binary to decimal conversion?

• It uses two digits 0 and 1.
• It is also called as base 2 number system.
• Here, each position in any binary number represents a power of the base (2). Example: 23
• The last position represents a y power of the base (2). Example: 2y where y represents the last position.

Example

Calculating the Decimal Equivalent of binary number −

2.    Explain binary addition?

Binary Addition

• It is a basis for binary subtraction, multiplication, division.
• There are four rules which are as follows:

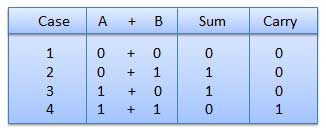
                                 Fig.1 Rules of Binary addition

In fourth step, a sum (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column is done.

For Example −

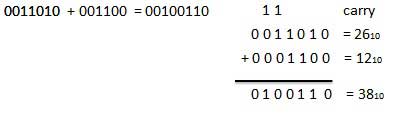
                                 Fig.2 Binary addition

3.    Explain binary subtraction?

Binary Subtraction

Subtraction and Borrow, these are the two words that will be used very frequently for binary subtraction. There rules of binary subtraction are:

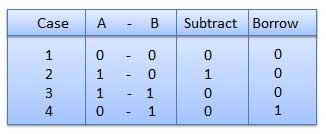
                                  Fig.3 Rules of Binary Subtraction

For Example

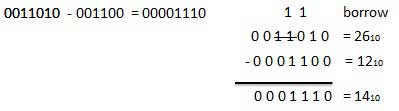
                                 Fig.4 Binary subtraction

4.    Explain binary multiplication?

Binary Multiplication

• It is similar to decimal multiplication.
• It is also simpler than decimal multiplication as only 0s and 1s are involved.
• There are four rules of binary multiplication which are:

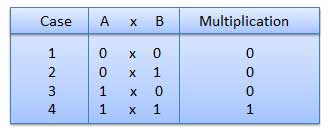
                             Fig.5 Rules of Binary Multiplication (Ref. 1)

For Example

                             Fig.6 Binary Multiplication

5.    Explain binary division?

Binary Division

• It is similar to decimal division.
• It is also called as the long division procedure.

For Example

                                       Fig.7 Binary Division

6.    Explain 1’s complement and two’s complement?

1's complement

• Here, a number is obtained by changing all 1's to 0's and all 0's to 1's.
• This is called as 1's complement.
• For Example :

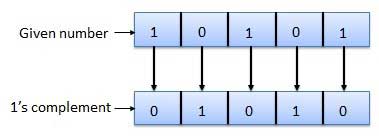
                                      Fig.8: 1's complement

2's complement

• It is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.
• Hence, 2's complement = 1's complement + 1
• For Example:

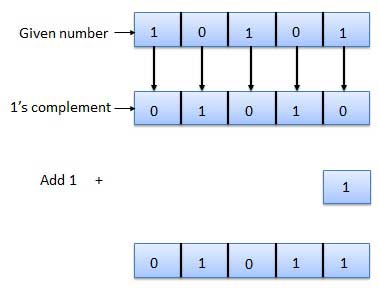
                                      Fig.9: 2's complement

7.    What is octal number system?

Octal Number System

• It consists of eight digits 0, 1,2,3,4,5,6,7.
• It is also named as base 8 number system.
• Here each position represents a power of the base (8). Example: 82

• The last position represents a y power of the base (8). Example: 8y where y represents the last position .

Example

Octal Number − 125758

Calculating Decimal Equivalent −

7.Explain octal addition and octal subtraction?

Octal Addition

The octal addition table is as follows:

                            Fig.10: Octal addition table

• To use the above table, simply follow the example:
• Add 68and 58.
• Locate 6 in the A column then locate the 5 in the B column.
• The point in 'sum' area where these two columns intersect is the 'sum' of two numbers.

68 + 58 = 138.

For Example :

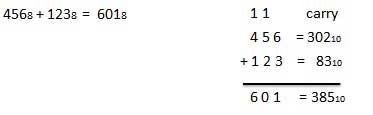
                            Fig.11: Octal addition (Ref. 1)

Octal Subtraction

• It follows the same rules as the subtraction of numbers in any other system.
• The only difference is in borrowed number.
• In the decimal system, we borrow a group of 1010.
• In the binary system, we borrow a group of 210.
• But in the octal system we borrow a group of 810.

For Example

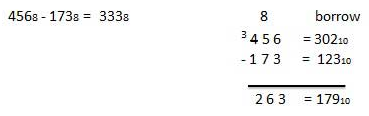
                            Fig.12: Octal subtraction (Ref. 1)

8.    Explain hexadecimal number system?

• It uses 10 digits starting from 0,1,2,3,4,5,6,7,8,9 and 6 letters A,B,C,D,E,F.
• These letters represents numbers as A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
• It is also known as base 16 number system.
• Here each position represents a power of the base (16). Example 161.
• The last position represents a y power of the base (16). Example: 16y where y represents the last position .

Example −

Hexadecimal Number: 19FDA16

Calculating Decimal Equivalent −

9.    Explain logic gates?

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

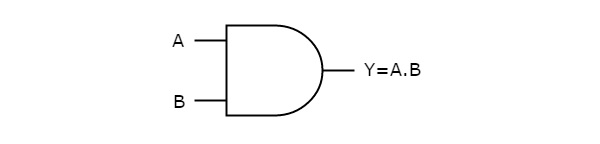
                                         Fig. : AND gate (ref. 1)

Timing Diagram:

OR gate

It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of 2-input OR gate is:

Here A, B are the inputs and Y is the output of two input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

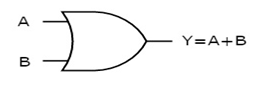
                                                     Fig. : OR gate (ref. 1)

Timing Diagram:

NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

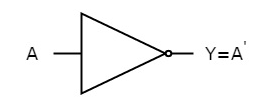
                                             Fig. : NOT gate (ref. 1)

Timing Diagram:

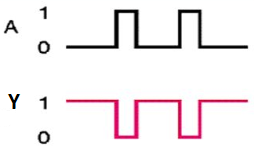
Universal gates

      NAND & NOR gates are known as universal gates.

      We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of 2-input NAND gate is:

Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

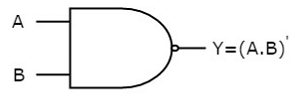
                                              Fig.: NAND gate (ref. 1)

NAND gate works same as AND gate followed by an inverter.

Timing Diagram:

NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the input is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.

The symbol of NOR gate is:

                                                  
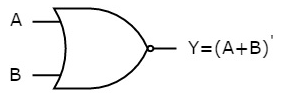
                                                           Fig.: NOR gate (ref. 1)

NOR gate works exactly same as that of OR gate followed by an inverter.

Timing Diagram:

10.           Write a note on special gates?

Ex-OR gate

It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

                                                           Fig.: XOR gate (ref. 1)

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

Ex-NOR gate

It stands for Exclusive-NOR gate. Its function is same as that of NOR gate except when the inputs having even number of ones.

The truth table of 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.

Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.

The symbol of Ex-NOR gate is:

                                       Fig.: XNOR gate (ref. 1)

It is similar to NOR gate except for few combination(s) of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.

Timing Diagram:

11.           Explain Boolean algebra?

• It deals with binary numbers & variables.
• Therefore, also known as Binary Algebra or logical Algebra.
• A mathematician named as George Boole had developed this algebra in 1854.
• The variables that are used in this algebra are known as Boolean variables.
• Considering the range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.

12.           Explain De Morgan’s theorem?

• It is useful in finding the complement of Boolean function.
• It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
• It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’.y’

• The dual of the above Boolean function is

(x.y)’ = x’ + y’

• Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.

Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.

13.           Simplify the expression

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification .

⇒ f = qr(1) + pr(1) + pq(1)

                                                                ⇒ f = qr + pr + pq

                                                                         ⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are same. As per requirement, we can choose one of them.