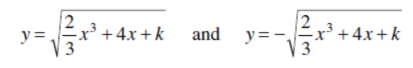UNIT 1
Ordinary differential equations
Question-1: Find the general solution of x 2 – 4x³
2 – 4x³
Solution: rearranging the given equation:
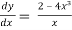 =
=  -
- 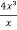 =
= 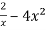
On integrating both sides,
y =  = 2 In x -
= 2 In x - 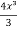 + c
+ c
Question-2: Find the particular solution of the differential equation 5 , given the boundary condition y = 1
, given the boundary condition y = 1 , when x = 2.
, when x = 2.
Solution: rearrange the diff. Equation,
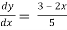 =
=  -
- 
y = 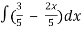 =
=  -
-  + c, which is the general solution.
+ c, which is the general solution.
Put the boundary conditions to find c,
1 -
-  , which gives, c = 1
, which gives, c = 1
Hence the particular solution is,
y =  -
- 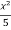 + 1.
+ 1.
Question-3: : Find the general solution of 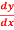 = 3 + 2y
= 3 + 2y
Solution: here,  = 3 + 2y gives,
= 3 + 2y gives,
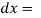
 ,
,
Integrating both sides,

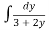 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Question-4: Determine the particular solution of (y² - 1) 3y given that y =1 when x = 2
3y given that y =1 when x = 2 .
.
Solution: It gives,


When putting the values, y =1 , x = 2 ,
,
The particular solution will be,

Question-5: Solve the equation 4xy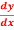 = y² - 1
= y² - 1
Solution: on separating variables, we get
( ) dy =
) dy =  dx
dx
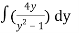 =
= 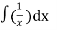
Using substitution, u = y² - 1
2In(y² - 1) = In x + c.
Question-6: Determine the particular solution of 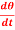 = 2
= 2 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
Solution:  = 2
= 2 = 2
= 2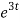
 ,
,
 = 2
= 2 dt
dt
 dθ =
dθ =  dt
dt
Now integrating both sides,
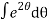 =
= 
The general solution is ,
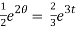 + c.
+ c.
When t = 0 and θ = 0, c = 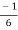
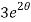 =
= 
Question-7: solve (6x² - y +3)dx + (3y² -x -2)dy = 0
Sol. First we check exactness,
 (3y² -x -2) = -1
(3y² -x -2) = -1
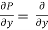 (6x² - y +3) = -1
(6x² - y +3) = -1
Hence this is an exact differential equation.
Write the system of equation to find h(x,y),
 = P(x,y) = (6x² - y +3)
= P(x,y) = (6x² - y +3)
 = Q(x,y) = (3y² -x -2)
= Q(x,y) = (3y² -x -2)
Integrate the first eq. w.r.t. x , assume y is constant,
h(x,y) = 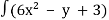 dx
dx
= 
= 2x³ - xy +3x +g(y)
Here we have continuous differentiable function g(y) instead of C.
Now,
 =
=  (2x³ - xy +3x +g(y))
(2x³ - xy +3x +g(y))
-x + g’(x) = 3y² - x – 2
We get,
g’(x) = 3y² – 2
Now integrate,
g(x) = 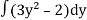 = y³ - 2y
= y³ - 2y
So,
h(x,y) = 2x³ -xy +3x +y³ -2y,
The general solution is defined by the following expression,
2x³ -xy +3x +y³ -2y = C
Question-8: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
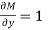

These are not equal results, so we can say that the given diff. Eq. Is not exact.
Question-9: solve  + xy = xy²
+ xy = xy²
Solution : here , n =2, so me make substitution,
y = 
y’ = 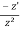
Now substitute these equations,
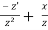 =
= 
Or z’ – zx = -x -----------(1)
this is the linear form of unknown function f(z),
Integrating factor is,
I(x) = 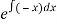 =
= 
Multiply (1) by I(x), we get

 - x
- x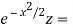 -x
-x
Or  = -x
= -x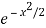
Integrating both sides,
 =
=  +c
+c
Z(x) = c
The solution for the original diff. Eq.
y =  .
.
Question-10: solve 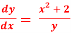 .
.
Solution: this can be written in differential form,
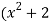 )dx – ydy = 0
)dx – ydy = 0
Which can be separated as ,
A(x) =  ) , B(y) = -y
) , B(y) = -y
Its solution is given by,
 -
- 
 x³ + 2x -
x³ + 2x -
Solving for y , we obtain the solution in implicit form,
y² =  x³ + 4x + k with k = -2c
x³ + 4x + k with k = -2c
Solving for y, we get,