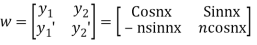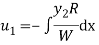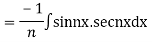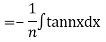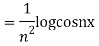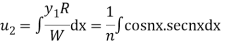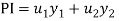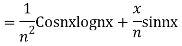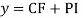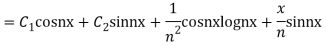Question Bank

Linear differential equations

Question-1:  Solve

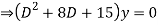
Ans. Given,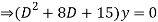

Here Auxiliary equation is

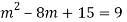
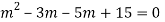
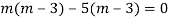
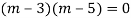
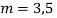
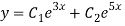
Question-2: solve

Ans. The auxiliary equation is

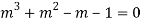
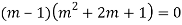
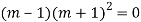
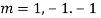
Hence the solution is

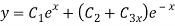
Question-3:  Solve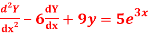 

Ans. Given,

Auxiliary equation is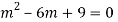

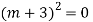
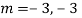
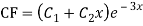
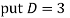
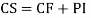
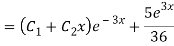
Question – 4:  Solve

Ans. The AE is

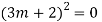
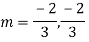
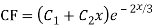
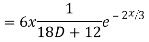
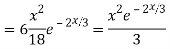
Complete solution y= CF + PI

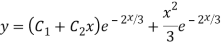
Question -5:

Ans. The AE is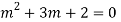

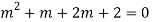
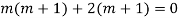
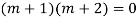
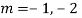
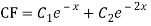
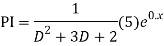
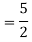
Complete solution = CF + PI

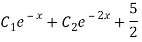
Question-6:  Solve

Ans. The AE is

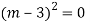
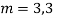
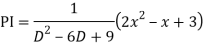
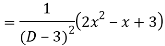
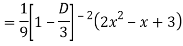
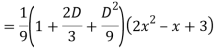
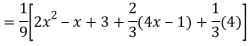
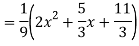
Complete solutio0n is y= CF + PI

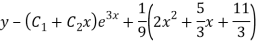
Question- 7:  Find the PI of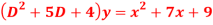

Ans.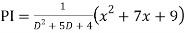

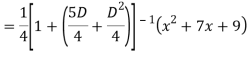
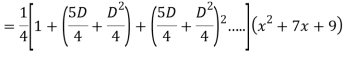
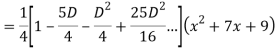
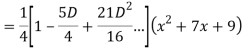
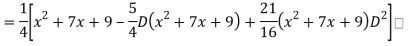
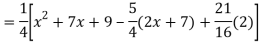
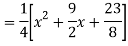
Question -8:  Solve

Ans. Given equation in symbolic form is

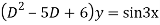
Its Auxiliary equation is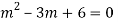

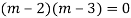
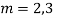
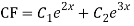
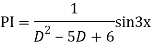
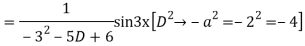
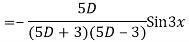
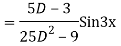
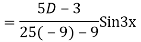
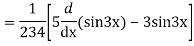
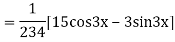
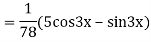
Complete solution is y= CF + PI

Question -9: Solve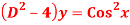

Ans. The AE is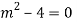

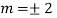
We know,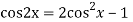

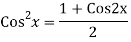
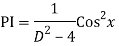
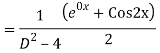
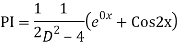
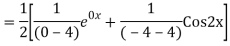
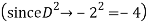
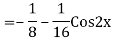
Complete solution is y= CF + PI

Question -10:  Solve (4D² +4D -3)y =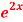 

 Auxiliary equation is 4m² +4m – 3 = 0

    We get,             (2m+3)(2m – 1) = 0

                               m =   ,

  complementary function:  CF is  A+ B

             now we will find particular integral,

                         P.I. = f(x)

                                =   .

                                =    .

                                  =    .

                                  =   . =   .

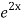
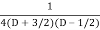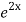
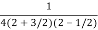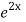      General solution is y =  CF + PI

                                                    = A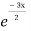+ B  .

Question -11:

Ans. Put,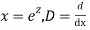

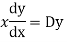
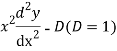
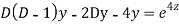
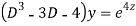
AE is

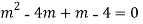
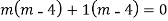
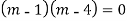
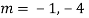
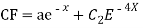
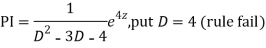
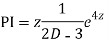
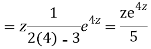
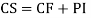
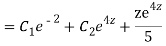
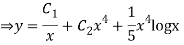
Question -12:  solve 

Ans. Let, so that z = log x

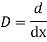
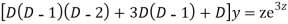
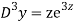
AE is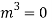

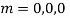
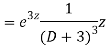
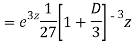
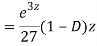
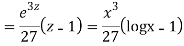
Question -13:  solve – y = 2x² - x – 3

Ans.: first we find general solution:

    The characteristic function is:   r² - 1 = 0

                                                            ( r-1)(r+1) = 0

                                                           R = 1, -1

General solution is -  A + B,

                  Now , let        

                                              y = ax² + bx +c

                                             = 2ax + b

                                            2a

Put these value in 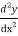 – y = 2x² - x – 3,

                           2a – (ax² + bx +c) = 2x² - x – 3

                           2a – ax² - bx - c = 2x² - x – 3

Now compare coeff.

 Coeff. Of x² ,    a = -2

Coeff. Of x ,      b = 1

Constant coeff.

                                 2a – c = -3,       c =-1

So the particular solution will be,

             y =  -2x² + x – 1

Complete solution is,

              y = A + B- 2x² + x – 1

Question -14   Solve

 here cf is  r² -6r +9 = 0

                                     (r – 3)² = 0

                                           r = 3

 so the general solution is - A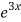 + B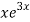

Now we will find particular solution,

  lets, y =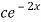

         =

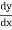Substitute these values,

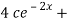
         + 9 =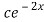

           =

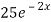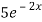
               C = 1/5

The particular solution is ,

                                        y = 1/5

 complete solution,

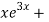                                       y = - A + B 1/5

Question -15:   Solve d2 y)/dx2+x2 y=sec nx

Ans. The AE is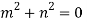

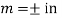
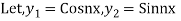
The Wronskian of 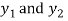is