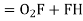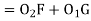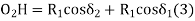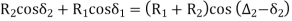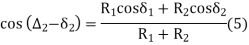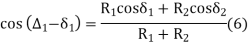S2
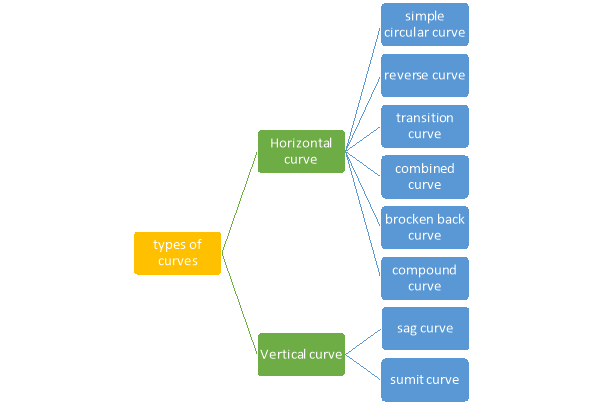
UNIT-5CURVE SETTINGQ1.What is curve and its necessity?A1) When two straight lines intersect at some angle then a curve is provided in between them which meets the straight line tangentially. Necessity (Curves are provided for the following reasons)Curves are needed on highways Railways and Canal for bringing about a gradual change of direction of motion to bring about gradual changes in direction of motion to connect important places to avoid obstructions to bring about gradual changes in grade and for good visibility to balance earthquake in acceleration cutting minimising construction cost Q2.What are the types of curves?
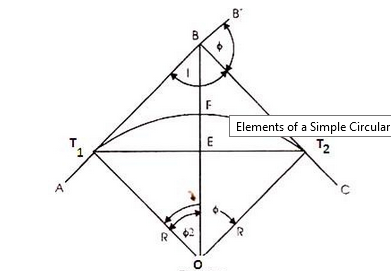
Q3.What are the element in simple curve?
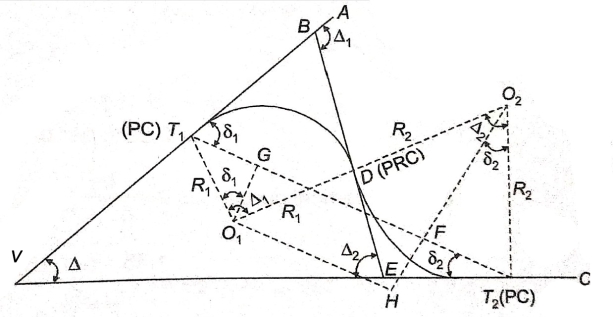
 Q4. What are the element in compound curve?A4) The compound curve has seven elements
Q4. What are the element in compound curve?A4) The compound curve has seven elements Radius R1, Radius R2, deflection angle φ, the deflection angle of the first arc φ1, the deflection angle of the second arc φ2, tangent length LT1 and LT2. Elements of Compound Curves Common tangent = MN = MD + DN = R1 tan (∆ 1 /2) + R2 tan (∆ 2 /2) ∆ = ∆ 1 + ∆ 2 Length of the main tangents IT1 and IT2: IT1 = T1M + MI = R1 tan ∆ 1 /2 + MN sin ∆ 2 /sin ∆ IT2 = T2N + NI = R2 tan ∆ 2 /2 + MN sin ∆ 1 /sin ∆ 2Q5.What is the relation between degree and radius of curve?A5) Arc definition of degree of the curve: According to this, degree of curve in the central angle subtended by an arc of the length of 20m or 30 m.If R = radius of curveD = degree of curve as per arc definition for 30m arc length.D° = 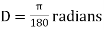 Q (radians) =
Q (radians) = 

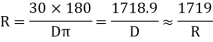
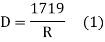 For 20 mm length
For 20 mm length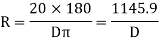
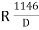 (2)Q6.What is setting out of compound curve?A6) Setting a compound curve
(2)Q6.What is setting out of compound curve?A6) Setting a compound curve Calculate all elements ∆1, ∆2, ∆, R1, R2, IT2 and IT1. Locate PI (I), PC (T1) and PT (T2) Calculate chainage of T1 (chainage of I – tangent length IT1) Calculate chainage of the point of compound curvature D. Chainage of D = Chainage of T1 + length of arc T1D = chainage of T1 + ΠR1 ∆1 / 180o Calculate chainage of T2 = chainage of D + ΠR2 ∆2 / 180o Calculate the deflection angles for both the arcs from their tangents, e.g. ∆1 = δ1 = 1719 C1 / R, where C1 is the chord length and R is the radius Q7.What is the setting out of simple curve?A7) Method of setting out curveThe linear method offset from long chord
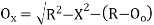
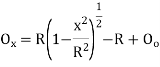
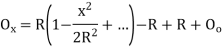
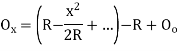
 Where
Where 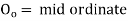
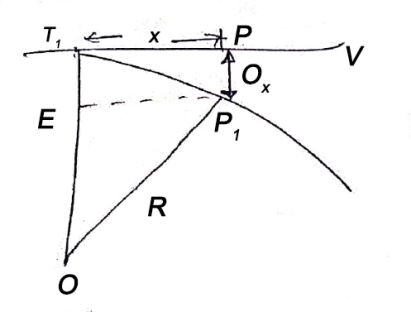
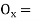 offset at some point P at distance x from midpoint D. (ii) Perpendicular offset from tangent
offset at some point P at distance x from midpoint D. (ii) Perpendicular offset from tangent
Fig-3 linear method offset from long chord
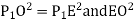
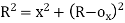
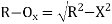
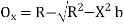

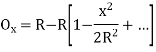
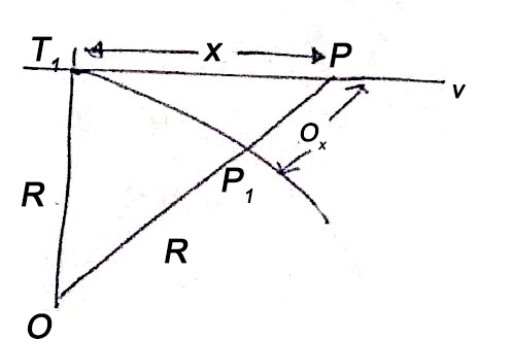
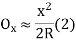 (iii) Radial offset from tangent:
(iii) Radial offset from tangent:
Fig-4 Radial offset from tangent: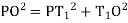
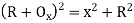
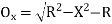
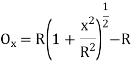
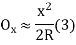 (iv) Successive Bisection of Arc or chord
(iv) Successive Bisection of Arc or chord
Fig-5 Successive Bisection of Arc or chord

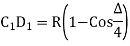
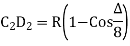 (v) By offset from chord produced
(v) By offset from chord produced 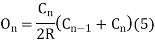
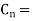 last sub chord b) Angular method i) Rankine's method of the deflection angle- It is generally used for setting out a circular curve of long length and large radius.- It gives good result except then chords are long as compared to a radius, so that variation between the length of an Arc and its cord becomes considerable.- It is used in highway and Railway
last sub chord b) Angular method i) Rankine's method of the deflection angle- It is generally used for setting out a circular curve of long length and large radius.- It gives good result except then chords are long as compared to a radius, so that variation between the length of an Arc and its cord becomes considerable.- It is used in highway and Railway
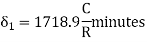
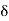 = Tangential angleC = chord length (ii) Tacheometric method-It is similar to Rankine’s method of deflection angle.- The theodolite at may be used as Tacheometric and Tacheometric observation are made.- Less accurate as compared to Rankins.- Chaining is completely dispersed in this method.
= Tangential angleC = chord length (ii) Tacheometric method-It is similar to Rankine’s method of deflection angle.- The theodolite at may be used as Tacheometric and Tacheometric observation are made.- Less accurate as compared to Rankins.- Chaining is completely dispersed in this method.
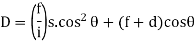 (For Incline and line of sight)
(For Incline and line of sight)
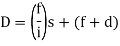 (For the horizontal line of sight)
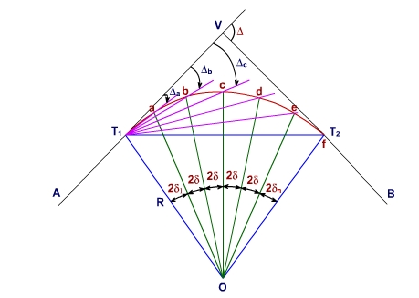
(For the horizontal line of sight)Two theodolite method Convenient than any of our method when the ground is undulating rough and not suitable for Linear measurements. Two theodolites are used and linear measurement is eliminated. Hence, the most accurate method. It is based on the principle that the angle between the tangent and chord is equal to the angle subtended by a chord in the opposite segment. Time-consuming method Most accurate method Highly expensive. Q8. What is the rankines deflection angle method?A8) In this method, curves are staked out by use of deflection angles turned at the point of curvature from tangent to points along the curve. The curve is set out by driving pegs at a regular interval equal to the length of a normal chord. Usually, sub-chords are provided at the beginning and end of the curve to adjust the actual length of the curve. The method is based on assumption that there is no difference between the length of the arcs and their corresponding chords of normal length or less. The underlying principle of this method is that deflection angle to any point on the circular curve is measured by one-half the angle subtended at the centre of the circle by the arc from the P.C. to that point. [Rule 1 under "Fundamentals of the geometry of the Circular Curve" stated in lesson 37]. Let pts a,b,c,d,e are to be identified in the field to lay out a curve between T1 and T2 to change direction from the straight alignment AV to VB .
Fig-6 Rankine’s deflection angle method To decide about points, chords ab, bc, cd, de are being considered having the nominal length of 30m. To adjust the actual length of curve two sub-chords have been provided one at the beginning, T1 a and other, eT2 at end of the curve. The number of deflection angles that are to be set from the tangent line at the P.C. is computed before setting out the points. The steps for computations are as follows:
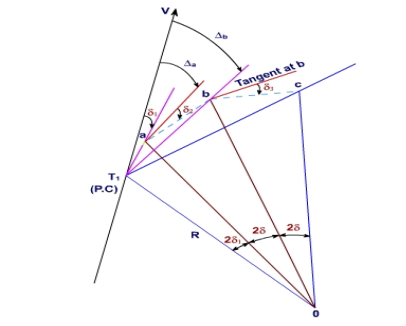
,Fig-7 Rankine’s deflection angle system let the tangential angles for points a, b, c,… be d1, d,…, d, dn and their deflection angles (from the tangent at P.C.) be Da, Db, ….., Dn. Arc T1 a = R x 2d1 radians Assuming the length of the arc is same as that of its chord if C1 is the length of the first chord i.e., chord T1 a, then 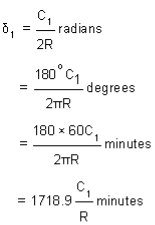 Reference -3 (Note: the units of measurement of chord and that of the radius of the curve should be same). Similarly, tangential angles for chords of nominal length, say C,
Reference -3 (Note: the units of measurement of chord and that of the radius of the curve should be same). Similarly, tangential angles for chords of nominal length, say C, 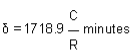 Reference -4 And for the last chord of length, say Cn
Reference -4 And for the last chord of length, say Cn 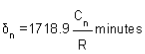 Reference -5 The deflection angles for the different points a, b, c, etc. can be obtained from tangential angles. For the first point a, deflection angle Da is equal to the tangential angle of the chord to this point i.e., d1. Thus, Da =d1. The deflection angle to next point i.e., b is Db for which the chord length is T1 b. Thus, the deflection angle
Reference -5 The deflection angles for the different points a, b, c, etc. can be obtained from tangential angles. For the first point a, deflection angle Da is equal to the tangential angle of the chord to this point i.e., d1. Thus, Da =d1. The deflection angle to next point i.e., b is Db for which the chord length is T1 b. Thus, the deflection angle 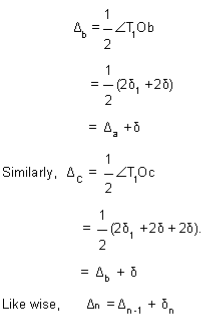 Reference -6Thus, the deflection angle for any point on the curve is deflection angle up to the previous point plus tangential angle at the previous point. Q9.What is reverse curve and given equation between 2 parallel straights?A9) In ∆BVE∆1 = ∆ + ∆2∆ = ∆1 - ∆2In ∆ T1VT2S1 = ∆ + S2∆ = S1 – S2∆1 - ∆2 = S1 – S2O1G ∥ O2P∆1 – S1 = ∆2 – S2∆1 - ∆2 = S1 – S2
Reference -6Thus, the deflection angle for any point on the curve is deflection angle up to the previous point plus tangential angle at the previous point. Q9.What is reverse curve and given equation between 2 parallel straights?A9) In ∆BVE∆1 = ∆ + ∆2∆ = ∆1 - ∆2In ∆ T1VT2S1 = ∆ + S2∆ = S1 – S2∆1 - ∆2 = S1 – S2O1G ∥ O2P∆1 – S1 = ∆2 – S2∆1 - ∆2 = S1 – S2
GF = O1H = (R1 + R2) sin (∆2 – δ2)T1T2 = T1G + GF + FT2 = R1 sin δ1 + (R1+ R2) sin (∆2 – δ2) + R2 sin δ2O2H = O2F + FH= O2F + FH = O2F + O1G= R2 cos δ1 + R1 cos δ1 ...............................(1)In ∆ O1O2 H O2H = (R1+ R2) cos (∆2 – δ2) ................................(2)From (1) and (2) R2 cos δ2 + R1 cos δ1 = (R1 + R2) cos ( ∆2 – δ2)
similarly
Q9.What is reverse curve and given equation between 2 parallel straights?A10) When to normal circular curves of different or equal radii, have opposite in direction of curvature join together, the formed or resultant curve is known as a reverse curve. Uses:-When the angle between the two straight lines is very small. When two straight lines are parallel to each other. The element of a reverse curve
Fig-10 Element of reverse curve- VA and ucinclude deviation angle of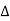 .-
.- 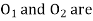 centres of two curve.-
centres of two curve.- 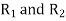 are radii of two curve.-
are radii of two curve.- 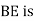 common tangent which is perpendicular to
common tangent which is perpendicular to 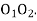 - Join
- Join 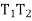 and draw
and draw 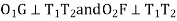 In ∆BVE,
In ∆BVE,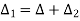
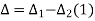 In
In 

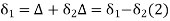 From (1) and (2)
From (1) and (2)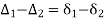
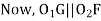
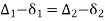
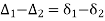 In,
In, 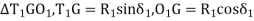 In,
In,
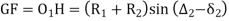
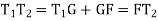
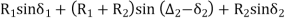
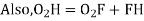
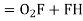
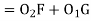
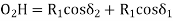 Also,
Also,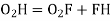
|
|
 Q4. What are the element in compound curve?A4) The compound curve has seven elements
Q4. What are the element in compound curve?A4) The compound curve has seven elements 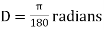 Q (radians) =
Q (radians) = 

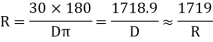
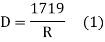 For 20 mm length
For 20 mm length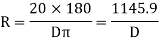
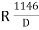 (2)Q6.What is setting out of compound curve?A6) Setting a compound curve
(2)Q6.What is setting out of compound curve?A6) Setting a compound curve 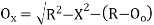
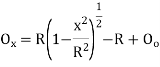
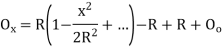
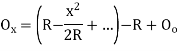
 Where
Where 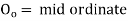
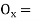 offset at some point P at distance x from midpoint D. (ii) Perpendicular offset from tangent
offset at some point P at distance x from midpoint D. (ii) Perpendicular offset from tangent
|
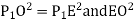
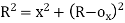
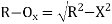
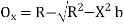

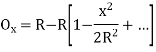
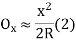 (iii) Radial offset from tangent:
(iii) Radial offset from tangent:
|
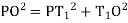
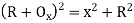
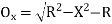
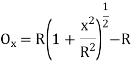
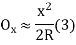 (iv) Successive Bisection of Arc or chord
(iv) Successive Bisection of Arc or chord
|

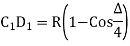
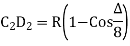 (v) By offset from chord produced
(v) By offset from chord produced 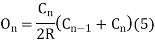
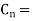 last sub chord b) Angular method i) Rankine's method of the deflection angle- It is generally used for setting out a circular curve of long length and large radius.- It gives good result except then chords are long as compared to a radius, so that variation between the length of an Arc and its cord becomes considerable.- It is used in highway and Railway
last sub chord b) Angular method i) Rankine's method of the deflection angle- It is generally used for setting out a circular curve of long length and large radius.- It gives good result except then chords are long as compared to a radius, so that variation between the length of an Arc and its cord becomes considerable.- It is used in highway and Railway 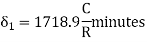
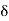 = Tangential angleC = chord length (ii) Tacheometric method-It is similar to Rankine’s method of deflection angle.- The theodolite at may be used as Tacheometric and Tacheometric observation are made.- Less accurate as compared to Rankins.- Chaining is completely dispersed in this method.
= Tangential angleC = chord length (ii) Tacheometric method-It is similar to Rankine’s method of deflection angle.- The theodolite at may be used as Tacheometric and Tacheometric observation are made.- Less accurate as compared to Rankins.- Chaining is completely dispersed in this method. 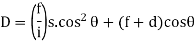 (For Incline and line of sight)
(For Incline and line of sight) 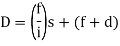 (For the horizontal line of sight)
(For the horizontal line of sight)
|
|
 Reference -3 (Note: the units of measurement of chord and that of the radius of the curve should be same). Similarly, tangential angles for chords of nominal length, say C,
Reference -3 (Note: the units of measurement of chord and that of the radius of the curve should be same). Similarly, tangential angles for chords of nominal length, say C, 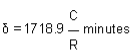 Reference -4 And for the last chord of length, say Cn
Reference -4 And for the last chord of length, say Cn 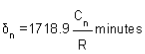 Reference -5 The deflection angles for the different points a, b, c, etc. can be obtained from tangential angles. For the first point a, deflection angle Da is equal to the tangential angle of the chord to this point i.e., d1. Thus, Da =d1. The deflection angle to next point i.e., b is Db for which the chord length is T1 b. Thus, the deflection angle
Reference -5 The deflection angles for the different points a, b, c, etc. can be obtained from tangential angles. For the first point a, deflection angle Da is equal to the tangential angle of the chord to this point i.e., d1. Thus, Da =d1. The deflection angle to next point i.e., b is Db for which the chord length is T1 b. Thus, the deflection angle 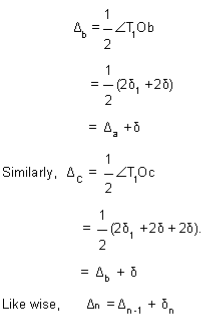 Reference -6Thus, the deflection angle for any point on the curve is deflection angle up to the previous point plus tangential angle at the previous point. Q9.What is reverse curve and given equation between 2 parallel straights?A9) In ∆BVE∆1 = ∆ + ∆2∆ = ∆1 - ∆2In ∆ T1VT2S1 = ∆ + S2∆ = S1 – S2∆1 - ∆2 = S1 – S2O1G ∥ O2P∆1 – S1 = ∆2 – S2∆1 - ∆2 = S1 – S2
Reference -6Thus, the deflection angle for any point on the curve is deflection angle up to the previous point plus tangential angle at the previous point. Q9.What is reverse curve and given equation between 2 parallel straights?A9) In ∆BVE∆1 = ∆ + ∆2∆ = ∆1 - ∆2In ∆ T1VT2S1 = ∆ + S2∆ = S1 – S2∆1 - ∆2 = S1 – S2O1G ∥ O2P∆1 – S1 = ∆2 – S2∆1 - ∆2 = S1 – S2In ∆T1GO1 T1G = R1 sin δ1 , O1G = R1 cos δ1 In ∆T2FO2 T2F = R2 sin δ2 , O2F = R2 cos δ2 |
cos ( ∆2 – δ2) = R2 cos δ2 + R1 cos δ1/ (R1 + R2) |
cos ( ∆1 – δ1) = R1 cos δ1 + R1 cos δ2/ (R1 + R2) |
|
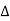 .-
.- 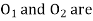 centres of two curve.-
centres of two curve.- 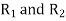 are radii of two curve.-
are radii of two curve.- 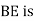 common tangent which is perpendicular to
common tangent which is perpendicular to 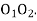 - Join
- Join 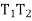 and draw
and draw 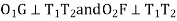 In ∆BVE,
In ∆BVE,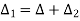
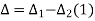 In
In 

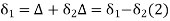 From (1) and (2)
From (1) and (2)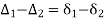
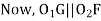
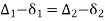
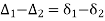 In,
In, 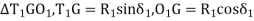 In,
In,
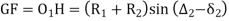
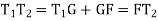
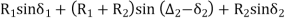
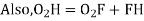
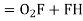
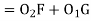
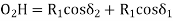 Also,
Also,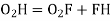
From (3) and (4)
|
0 matching results found