CO
UNIT-6Arithmetic Q1) Explain addition and subtraction of signed numbers.A1) The addition and subtraction algorithm for data represented in signed magnitude and again data represented in signed 2’s complement.It is important to realize that the adopted representation for negative numbers refers to the representation of numbers in the register before and after the execution of the arithmetic operations. We designate the magnitude of the two numbers by A and B. Where the signed numbers are added or subtracted, we find that there are eight different conditions to consider, depending on the sign of the numbers and the operation performed.
Table 1.1 Addition and subtraction of signed-Magnitude numbers Q2) What is hardware implementation in arithmetic?A2) Hardware ImplementationTo implement the two arithmetic operations with hardware, it is first necessary that the two numbers be stored in registers. Let A and B be two registers that hold the magnitude of the numbers and AS BS be two flip flops that holds the corresponding sign. The results of the operation may be transferred to a third register. Consider the hardware implementation of the algorithm, a parallel adder is needed to perform the micro-operation A+B, a comparator circuit is needed to establish if A>B, A=B OR A<B and two parallel sub tractor circuits are needed to perform the micro-operation A-B and B-A.
Q3) Explain hardware algorithmA3) Hardware Algorithm
Flowchart is shown in figure, two signs A and B are compared by an exclusive OR gate, if the output is 0 the signs are identical and if it is 1 signs are different. Identical signs dictate that the magnitudes be added for an add operation. Different signs dictate that the magnitude be subtracted for a subtract operation. The magnitudes are added with a micro-operation EA A + B, where EA is a register that combines E and A. The carry in E after the addition constitutes an overflow if it is equal to 1. The value of E is transferred into the add-overflow flip-flop AVF. The two magnitudes are subtracted if the signs are different for an add operation or identical for a subtract operation. The magnitudes are subtracted by adding A to the 2's complemented B. No overflow can occur if the numbers are subtracted so AVF is cleared to 0. 1 in E indicates that A >= B and the number in A is the correct result. If this numbs is zero, the sign A must be made positive to avoid a negative zero. 0 in E indicates that A < B. For this case it is necessary to take the 2's complement of the value in A. The operation can be done with one micro-operation A =A' +1. we assume that the A register has circuits for micro-operations complement and increment, so the 2's complement is obtained from these two micro-operations. In other paths of the flowchart, the sign of the result is the same as the sign of A. so no change in A is required. However, when A < B, the sign of the result is the complement of the original sign of A. It is then necessary to complement A, to obtain the correct sign. The final result is stored in register A and its sign in As. The value in AVF indicates an overflow indication.
|
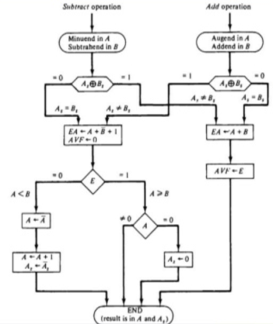
| Subtract Magnitudes |
|
|
Operation | Add magnitudes | When A>B | When A<B | When A=B |
(+A)+(+B) | +(A+B) |
|
|
|
(+A)+(-B) |
| +(A-B) | -(B-A) | +(A-B) |
(-A)+(-B) |
| -(A-B) | +(B-A) | +(A-B) |
(-A)+(-B) | -(A+B) |
|
|
|
(+A)-(+B) |
| +(A-B) | -(B-A) | +(A-B) |
(+A)-(-B) | +(A+B) |
|
|
|
(-A)-(+B) | -(A+B) |
|
|
|
(-A)- (-B) |
| -(A-B) | +(B-A) | +(A-B) |
|
|
Q4) Explain Design of fast Adders in detailA4) To reduce the computation time, there are faster ways to add two binary numbers by using carry lookahead adders. They work by creating two signals P and G known to be Carry Propagator and Carry Generator. The carry propagator is propagated to the next level whereas the carry generator is used to generate the output carry, regardless of input carry. The block diagram of a 4-bit Carry Lookahead Adder is shown here below -
The number of gate levels for the carry propagation can be found from the circuit of full adder. The signal from input carry Cin to output carry Cout requires an AND gate and an OR gate, which constitutes two gate levels. So if there are four full adders in the parallel adder, the output carry C5 would have 2 X 4 = 8 gate levels from C1 to C5. For an n-bit parallel adder, there are 2n gate levels to propagate through.Design Issues:The corresponding Boolean expressions are given here to construct a carry lookahead adder. In the carry-lookahead circuit we ned to generate the two signals carry propagator(P) and carry generator(G),
Having these we could design the circuit. We can now write the Boolean function for the carry output of each stage and substitute for each Ci its value from the previous equations:
|
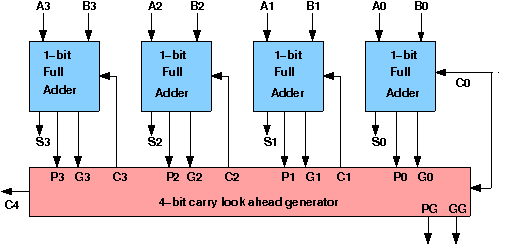
Pi = Ai ⊕ Bi Gi = Ai · Bi The output sum and carry can be expressed as Sumi = Pi ⊕ Ci Ci+1 = Gi + (Pi · Ci) |
C1 = G0 + P0 · C0 C2 = G1 + P1 · C1 = G1 + P1 · G0 + P1 · P0 · C0 C3 = G2 + P2 · C2 = G2 P2 · G1 + P2 · P1 · G0 + P2 · P1 · P0 · C0 C4 = G3 + P3 · C3 = G3 P3 · G2 P3 · P2 · G1 + P3 · P2 · P1 · G0 + P3 · P2 · P1 · P0 · C0 |
Q5) Explain Multiplication of Positive numbersA5) Multiplication of two fixed point binary numbers in signed magnitude representation consists of successive shift and addition operation.
If the multiplier bit is a 1, the multiplicand is copied down; otherwise, Zero are copied down Hardware Implementation for Signed Magnitude DataWhen multiplication is implemented in a digital computer it is convenient to change the process, instead of providing register to store and add same number of binary numbers and bits in the multiplier and instead of shifting the multiplicand to the left the partial product is shifted to the right. Hardware of multiplication consists of two or more registers; multiplier is stored in the Q register and its sign in Qs. Sequence counter is initially set to a number equal to the number of bits in the multiplier; the counter is decremented by 1 after forming each partial product. The sum of A and B forms a partial product which is transferred to the EA register.
Q6) What is Booth Multiplication Algorithm?A6) Booth Multiplication AlgorithmBooth algorithm is used for multiplying binary integers in signed 2’s complement representation
Q7) Explain Array MultiplierA7) The multiplication of the two binary numbers can be done with one micro-operation by means of a combinational circuit that forms the products at once
Q8) What is flowchart of multiplication?A8) Flowchart of Multiplication:
Initially multiplicand is stored in B register and multiplier is stored in Q register. Sign of registers B (Bs) and Q (Qs) are compared using XOR functionality (i.e., if both the signs are alike, output of XOR operation is 0 unless 1) and output stored in As (sign of A register). Note: Initially 0 is assigned to register A and E flip flop. Sequence counter is initialized with value n, n is the number of bits in the Multiplier.3. Now least significant bit of multiplier is checked. If it is 1 add the content of register A with Multiplicand (register B) and result is assigned in A register with carry bit in flip flop E. Content of E A Q is shifted to right by one position, i.e., content of E is shifted to most significant bit (MSB) of A and least significant bit of A is shifted to most significant bit of Q. 4. If Qn = 0, only shift right operation on content of E A Q is performed in a similar fashion. 5. Content of Sequence counter is decremented by 1. 6. Check the content of Sequence counter (SC), if it is 0, end the process and the final product is present in register A and Q, else repeat the process. Q9) Give an example of multiplicationA9) Multiplicand = 10111Multiplier = 10011
Q10) Write steps of working on the Booth AlgorithmA10) Working on the Booth AlgorithmSet the Multiplicand and Multiplier binary bits as M and Q, respectively. Initially, we set the AC and Qn + 1 registers value to 0. SC represents the number of Multiplier bits (Q), and it is a sequence counter that is continuously decremented till equal to the number of bits (n) or reached to 0. A Qn represents the last bit of the Q, and the Qn+1 shows the incremented bit of Qn by 1. On each cycle of the booth algorithm, Qn and Qn + 1 bits will be checked on the following parameters as follows: The operation continuously works till we reached n - 1 bit in the booth algorithm. Results of the Multiplication binary bits will be stored in the AC and QR registers.
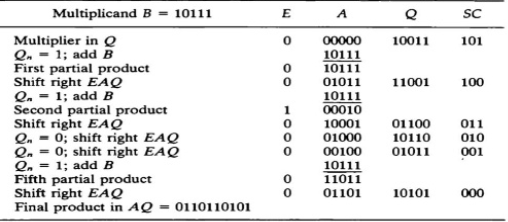
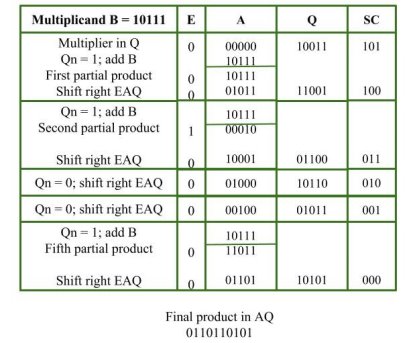
To multiply (23) and (19)
(23) 10111(Multiplicand)
10111 10111 00000 + 00000 10111
(437) 110110101 Product |
|
|
|
|
|
|
|
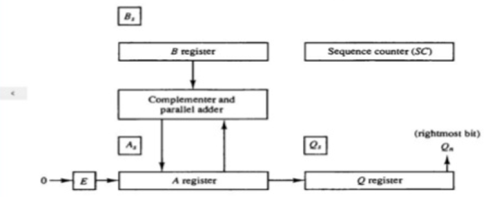
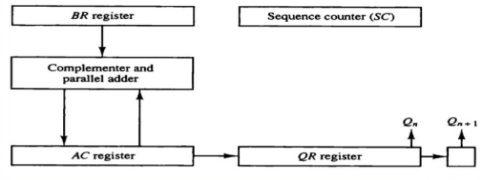
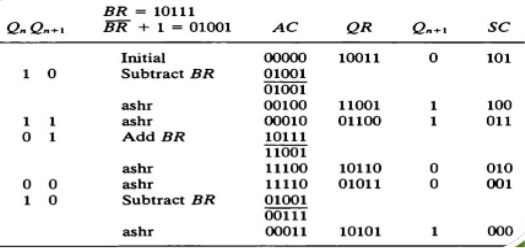
- When two bits Qn and Qn + 1 are 00 or 11, we simply perform the arithmetic shift right operation (ashr) to the partial product AC. And the bits of Qn and Qn + 1 is incremented by 1 bit.
- If the bits of Qn and Qn + 1 is shows to 01, the multiplicand bits (M) will be added to the AC (Accumulator register). After that, we perform the right shift operation to the AC and QR bits by 1.
- If the bits of Qn and Qn + 1 is shows to 10, the multiplicand bits (M) will be subtracted from the AC (Accumulator register). After that, we perform the right shift operation to the AC and QR bits by 1.
0 matching results found