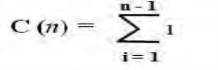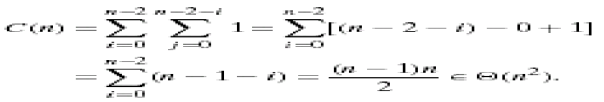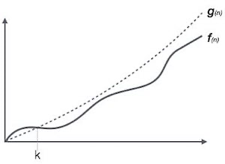
undefined | unit 1 introduction

DAA

Unit 1Introduction Q1) Explain the algorithm and various stages also?A1) Algorithm Basically, algorithms are the finite steps to solve problems in computers.It can be the set of instructions that performs a certain task.The collection of unambiguous instructions occurring in some specific sequence and such a procedure should produce output for a given set of input in a finite amount of time is known as Algorithm.In addition, all algorithms must satisfy the following criteria:● input: can be zero or more input● output: must produce output● finiteness: must have ending● definiteness: unambiguous and clear● effectiveness: should not be complex

A finite set of steps, each of which may require one or more operations, is composed of an algorithm. The probability of these operations being performed by a machine demands that certain restrictions be imposed on the type of operations that an algorithm might include. The fourth criterion we assume in this book for algorithms is that after a finite number of operations, they terminate.Criterion 5 demands that each process be efficient; each step must be such that a person using pencil and paper can do it in a finite amount of time, at least in theory. An example of successful operation is the output of arithmetic on integers, but arithmetic with real numbers is not, since certain values can only be represented by infinitely long decimal expansion. The efficacy property will be violet when adding two such numbers.● Computational procedures are often called algorithms that are definite and efficient.● The same algorithm can be interpreted in many ways by the same algorithm.● Many algorithms to answer the same problem● Various different speed definitions Q2) Write the various asymptotic notations?A2) Asymptotic notation Following are the asymptotic notations which are used to calculate the running time complexity of algorithm:

Big Oh (O) notation

Big Omega (ῼ) notation

Theta (Ꙫ) notation

Big Oh (O) Notation:● It is the formal way to express the time complexity.● It is used to define the upper bound of an algorithm’s running time.● It shows the worst case time complexity or largest amount of time taken by the algorithm to perform a certain task.

Fig: Big Oh notation

Here, f( n ) <= g( n ) ……………..(eq1)

where n>= k , C>0 and k>=1

if any algorithm satisfies the eq1 condition then it becomes f ( n )= O ( g ( n ) )

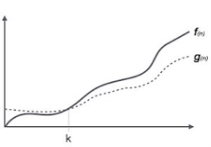
Big Omega (ῼ) Notation● It is the formal way to express the time complexity.● It is used to define the lower bound of an algorithm’s running time.● It shows the best case time complexity or best of time taken by the algorithm to perform a certain task.

Fig: Big omega notation

Here, f ( n ) >= g ( n )

where n>=k and c>0, k>=1

if any algorithm satisfies the eq1 condition then it becomes f ( n )= ῼ ( g ( n ) )

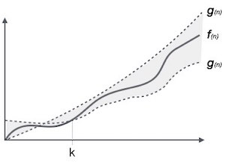
Theta (Θ) Notation● It is the formal way to express the time complexity.● It is used to define the lower as well as upper bound of an algorithm’s running time.● It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.

Fig: Theta notation

Let C1 g(n) be upper bound and C2 g(n) be lower bound.

C1 g(n)<= f( n )<=C2 g(n)

Where C1, C2>0 and n>=k

Q3) Write the different cases and analyses the condition of analysis?A3) Analyze the conditions:Following are the conditions where we can analyze the algorithm:● Time efficiency: indicates how fast algorithm is running● Space efficiency: how much extra memory the algorithm needs to complete its execution● Simplicity: generating sequences of instruction which are easy to understand.● Generality: It fixes the range of inputs it can accept. The generality of problems which algorithms can solve.Case of algorithm:As the algorithm has three cases according to time taken by program to perform a certain task.

Worst case: Performance (number of times performed by the specific operation) for Input of the worst-case size n. I.e.-I.e. Of all possible inputs of size n, the algorithm runs the longest.

2. Best case: Performance (number of times performed by the specific operation) for the Input best case size n. I.e.-I.e. Among all possible inputs of size n, the algorithm runs the fastest. 3. Average case: Average time taken (number of times it would take for the basic operation Executed) to address all possible instances of the input (random). Q4) Explain Mathematical analysis of Non recursive algorithm?A4) Mathematical analysis (Time efficiency) of Non recursive algorithm General plan for analyzing efficiency of non-recursive algorithms:

Decide on parameter n indicating input size

Identify algorithm ‘s basic operation

Check whether the number of times the basic operation is executed depends only on the input size n. If it also depends on the type of input, investigate worst, average, and best-case efficiency separately.

Set up summation for C(n) reflecting the number of times the algorithm ‘s basic operation is executed.

Simplify summation using standard formulas.

Example 1:Finding the largest element in a given array

ALGORITHM MaxElement(A[0..n-1])

//Determines the value of largest element in a given array

//Input: An array A[0..n-1] of real numbers

//Output: The value of the largest element in A

currentMax ← A[0]

for i ← 1 to n - 1 do

if A[i] > currentMax

currentMax ← A[i]

return currentMax

Analysis :

Input size: number of elements = n (size of the array)
Basic operation :

● Comparison

● Assignment

3. No best, worst, average cases.

4. Let C (n) denotes number of comparisons: Algorithm makes one comparison on each execution of the loop, which is repeated for each value of the loop‘s variable I within the bound between 1 and n – 1.

5. Simplify summation using standard formula

Example 2: Element uniqueness problem

Algorithm UniqueElements (A[0..n-1])

//Checks if all elements are distinct in a given array

//Input: An array A[0..n-1]

//Output: If all the elements in A are distinct and false otherwise, returns true

for i 0 to n - 2 do

for j i + 1 to n – 1 do

if A[i] = = A[j]

return false

return true

Analysis

Input size: number of elements = n (size of the array)
Basic operation: Comparison
Best, worst, average cases EXISTS.

An array giving the largest comparisons is the worst case input.

● Array without identical elements

● The only pair of equivalent elements is the series of the last two elements.

4. In the worst case, let C(n) denote the number of comparisons: for each repetition of the innermost loop, the algorithm makes one comparison, i.e., for each value of the loop variable j between its limits I + 1 and n-1; and this is repeated for each value of the outer loop, i.e. for each value of the loop variable I between its limits 0 and n-2.

5. Simplify summation

Q5) Explain Mathematical analysis of a recursive algorithm?A5) Mathematical analysis (time efficiency) of recursive algorithm General plan for analyzing efficiency of recursive algorithms:

Decide on the n parameter that indicates the input size.

Identify the basic operation of an algorithm.

Check that the number of times the basic operation is performed depends only on the size of the input n. If it also relies on the type of input, separately investigate worst, average, and best case performance.

Set up a recurrence relationship for the number of times the basic operation of the algorithm is executed, with a suitable initial condition.

Solve the repetition.

Example 1: Factorial function

ALGORITHM Factorial (n)

//Computes n! recursively

//Input: A nonnegative integer n

//Output: The value of n!

if n = = 0

return 1

else

return Factorial (n – 1) * n

Analysis

1. Input size: given number = n

2. Basic operation: multiplication

3. NO best, worst, average cases.

4. Let M (n) is number of multiplications.

M (n) = M (n – 1) + 1

for n > 0 M (0) = 0 initial condition

Where, M (n – 1) : to compute Factorial (n – 1)

1 :to multiply Factorial (n – 1) by n

5. Resolve the recurrence: Resolving using "Method of backward substitution":

M (n) = M (n – 1) + 1

= [ M (n – 2) + 1 ] + 1

= M (n – 2) + 2

= [ M (n – 3) + 1 ] + 3

= M (n – 3) + 3 …

In the ith recursion, we have

= M (n – i ) + i

When i = n, we have

= M (n – n ) + n = M (0 ) + n

Since M (0) = 0 = n

M (n) = Θ (n)

Example 2: In the binary representation of a positive, find the number of binary digits Decimal Integer Integers

ALGORITHM BinRec (n)

//Input: A positive decimal integer n

//Output: In n”s binary representation, the number of binary digits

if n = = 1

return 1

else

return BinRec (└ n/2 ┘) + 1

Analysis

Input size: given number = n
Basic operation: addition
NO best, worst, average cases.
Let A (n) denote the number of additions.

A (n) = A (└ n/2 ┘) + 1 for n > 1

A (1) = 0 initial condition

Where: A (└ n/2 ┘) : to compute BinRec (└ n/2 ┘)

1: to increase the returned value by 1

5. Solve the recurrence:

A (n) = A (└ n/2 ┘) + 1 for n > 1

Assume n = 2k (smoothness rule)

A (2k ) = A (2k-1) + 1 for k > 0; A (20) = 0

Solving using "Method of backward substitution":

A (2k ) = A (2k-1) + 1

= [A (2k-2) + 1] + 1

= A (2k-2) + 2

= [A (2k-3) + 1] + 2

= A (2k-3) + 3 …

In the recursion of ith, may have

= A (2k-i) + i

When i = k, we have

= A (2k-k) + k = A (20 ) + k

Since A (20 ) = 0

A (2k ) = k

Since n = 2k ,

HENCE k = log2 n

A (n) = log2 n

A (n) = Θ ( log n)

Q6) What is selection sort?A6) Selection Sort Sorting Problem The approach of brute force to sortingProblem: Rearrange them in non-decreasing order, given the list of n orderable objects (e.g., numbers, characters from some alphabet, strings of characters).Selection Sort

ALGORITHM SelectionSort(A[0..n - 1])

//The algorithm sorts a given array by selection sort

//Input: An array A[0..n - 1] of orderable elements

//Output: Array A[0..n - 1] sorted in ascending order

for i=0 to n - 2 do

min=i

for j=i + 1 to n - 1 do

if A[j ]<A[min] min=j

swap A[i] and A[min]

Example:

| 89 45 68 90 29 34 17

17 | 45 68 90 29 34 89

17 29 | 68 90 45 34 89

17 29 34 | 90 45 68 89

17 29 34 45 | 90 68 89

17 29 34 45 68 | 90 89

17 29 34 45 68 89 | 90

Explanation: Service of selection sorting on list 89, 45, 68, 90, 29, 34, 17. Each line corresponds to one iteration of the algorithm, i.e., a move through the tail of the list to the right of the vertical bar; the smallest element found is indicated by an element in bold. Elements to the left of the vertical bar are in their final positions and in this and subsequent iterations they are not considered.Performance analysis of selection sort algorithm :-The size of the input is given by the number of elements of n.The fundamental operation of the algorithm is the A[j]<A[min] primary contrast. The number of times it is run depends only on the size of the array and is given by

Thus, on all inputs, the selection form is an O(n2) algorithm. Only O(n) or, more specifically, n-11 is the number of key swaps (one for each repetition of the I loop). This property positively differentiates the form of selection from many other sorting algorithms. Q7) Explain bubble sort?A7) Bubble Sort Compare and swap adjacent elements of the list if they are out of order. After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.

Algorithm

BubbleSort(A[0..n - 1])

//The algorithm sorts array A[0..n - 1] by bubble sort

//Input: An array A[0..n - 1] of orderable elements

//Output: Array A[0..n - 1] sorted in ascending order

for i=0 to n - 2 do

for j=0 to n - 2 - i do

if A[j + 1]<A[j ]

swap A[j ] and A[j + 1

Example :

89 ↔️ 45 68 90 29 34 17

45 89 ↔️ 68 90 29 34 17

45 68 89 ↔️ 90 ↔️ 29 34 17

45 68 89 29 90 ↔️ 34 17

45 68 89 29 34 90 ↔️ 17

45 68 89 29 34 17 |90

45 ↔️ 68 ↔️ 89 ↔️ 29 34 17 |90

45 68 29 89 ↔️ 34 17 |90

45 68 29 34 89 ↔️ 17 |90

45 68 29 34 17 |89 90

Explanation: The first 2 bubble style passes are mentioned as 89, 45, 68, 90, 29, 34, 17. After a swap of two elements is completed, a new line is seen. The elements to the right of the vertical bar are in their final position and are not taken into account in the algorithm's subsequent iterations.Performance analysis of bubble sort algorithm:Clearly, there are n times of the outer loop. In this analysis, the only difficulty is in the inner loop. If we think of a single time the inner loop loops, by remembering that it can never loop more than n times, we can get a clear bound. Since the outer loop can complete n times with the inner loop, the comparison should not take place more than O(n2) times.For all arrays of size n, the number of key comparisons for the bubble sort version given above is the same.

It depends on the feedback for the number of key swaps. It's the same as the number of primary comparisons, for the worst case of declining arrays.

Observation: If no trades are made by going through the list, the list is sorted and we can stop the algorithm.While the new version runs on certain inputs faster, in the worst and average situations, it is still in O(n2). The type of bubble is not very useful for a large input set. How easy it is to code the type of bubble.Basic Message from Brute Force Method A first use of the brute-force method often results in an algorithm that can be strengthened with a small amount of effort. Compare successive elements of a given list with a given search key until either a match is found (successful search) or the list is exhausted without finding a match (unsuccessful search). Q8) What do you mean by brute force string matching?A8) Brute - force String MatchingProvided a string of n characters called a text and a string of m characters (m = n) called a pattern, find a text substring that matches the pattern. We want to find I the index of the leftmost character of the first matching substring in the text, to put it more specifically, so that

ti = p0 , …….., ti+j = pj ,........, ti+m-1 = pm-1 :

t0 …….ti ……..ti+j …...ti+m-1 ….tn-1 text T

p0 … pj ….. pm-1 pattern P

Pattern : 001011

Text : 10010101101001100101111010

2. Pattern : happy

Text : It's never too late to be happy childhood.

N O B O D Y _ N O T I C E D _ H I M

N O T

After a single character comparison, the algorithm almost always changes the pattern. In the worst case, before changing the pattern, the algorithm may need to make all m comparisons, and this can happen with any of the n - m + 1 attempts. In the worst case, thus, the algorithm is in (nm).Brute - force algorithm Calculate the distance between each pair of separate points and return the indexes of the points where the distance is smallest for them.

Algorithm BruteForceClosestPoints(P)

// Input : A list P of n (n ≥ 2) points P1 = (x1 , y1) ,........, Pn = (xn , yn)

// Output : Indicates index1 and index2 of the closet pair of points

dmin ← ∞

for i ← 1 to n - 1 do

for j ← i + 1 to n do

d ← sqrt((xi - xj)2 + (yi - yj)2 ) // sqrt is the square root function

if d < dmin

dmin ← d ; index1 ← i ; index2 ← j

Return index1, index2

Q9) Write an algorithm for sequential search?A9) Sequential Search

ALGORITHM SequentialSearch2(A [0..n], K)

//With a search key as a // sentinel, the algorithm implements sequential search

//Input: An array A of n elements and a search key K

//Output: The position of the first element in A[0..n - 1] whose value is

// equal to K or -1 if no such element is found

A[n]=K i=0

while A[i] = K do

i=i + 1

if i < n

return i

else return

Q10) what is brute force?A10) Brute - force Brute force is a basic approach to problem solving, usually explicitly based on the statement of the problem and definitions of the principles involved. The brute-force approach should not be ignored as a tactic, although rarely a source of clever or algorithms, brute force is applicable to a very wide range of problems. The brute-force method generates rational algorithms with at least some functional value with no constraint on example for some important problems (e.g. sorting, searching, string matching) Size.A brute-force algorithm can still be useful for solving small-size instances of a problem, even though too inefficient in general. A brute force algorithm can serve as an important theoretical or educational algorithm.

Sign Up