|
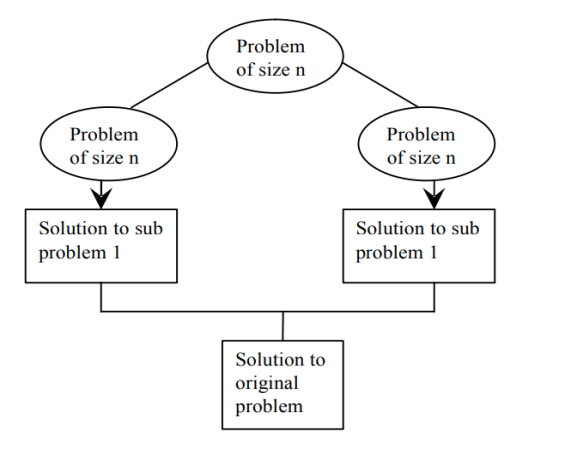
T(n) = aT(n/b) + f(n)
|
|
solve T(n) = 2T(n/2) + 1, using master theorem. Sol : Here, a = 2 b = 2 f(n) = Θ(1) d = 0 Therefore: a > bd i.e., 2 > 20 Case 3 of master theorem holds good. Therefore: T(n) Є Θ (nlog b a ) Є Θ (nlog 2 2 ) Є Θ (n)
|
Step 4: As each sub list gets the single element compare all the elements with each other & swap in between the elements.Step 5: merge the elements same as divide phase to get the sorted list Q6) Write an algorithm for quick sort?A6) Algorithm of Quick Sort
ALGORITHM Quicksort (A[ l …r ]) //sorts by quick sort //i/p: A sub-array A[l..r] of A[0..n-1],defined by its left and right indices l and r //o/p: The sub-array A[l..r], sorted in ascending order if l < r Partition (A[l..r]) // s is a split position Quicksort(A[l..s-1]) Quicksort(A[s+1..r] ALGORITHM Partition (A[l ..r]) //Partitions a sub-array by using its first element as a pivot //i/p: A sub-array A[l..r] of A[0..n-1], defined by its left and right indices l and r (l <r) //o/p: A partition of A[l..r], with the split position returned as this function‘s value p→A[l] i→l j→r + 1; Repeat repeat i→i + 1 until A[i] >=p //left-right scan repeat j→j – 1 until A[j] < p //right-left scan if (i < j) //need to continue with the scan swap(A[i], a[j]) until i >= j //no need to scan swap(A[l], A[j]) return j |
Best Case | O (n log n) |
Worst Case | O (n2) |
Average Case | O (n log n ) |
ALGORITHM Mergesort ( A[0… n-1] ) //sorts array A by recursive mergesort //i/p: array A //o/p: sorted array A in ascending order if n > 1 copy A[0… (n/2 -1)] to B[0… (n/2 -1)] copy A[n/2… n -1)] to C[0… (n/2 -1)] Mergesort ( B[0… (n/2 -1)] ) Mergesort ( C[0… (n/2 -1)] ) Merge ( B, C, A ) ALGORITHM Merge ( B[0… p-1], C[0… q-1], A[0… p+q-1] ) //merges two sorted arrays into one sorted array //i/p: arrays B, C, both sorted //o/p: Sorted array A of elements from B & C I →0 j→0 k→0 while i < p and j < q do if B[i] ≤ C[j] A[k] →B[i] i→i + 1 else A[k] →C[j] j→j + 1 k→k + 1 if i == p copy C [ j… q-1 ] to A [ k… (p+q-1) ] else copy B [ i… p-1 ] to A [ k… (p+q-1) ]
|
|
Analysis of merge sort: All cases having same efficiency as: O (n log n) T (n) =T ( n / 2 ) + O ( n ) T (1) = 0 Space requirement: O (n) Advantages ● The number of comparisons carried out is almost ideal. ● Mergesort is never going to degrade to O (n2) ● It is applicable to files of any size. Limitations ● Using extra memory O(n).
|
This process continues until the key element is found. If there is no key element present in the given array then its searches fail. Algorithm
Algorithms can be implemented as algorithms that are recursive or non-recursive. ALGORITHM BinSrch ( A[0 … n-1], key) //implements non-recursive binary search //i/p: Array A in ascending order, key k //o/p: Returns position of the key matched else -1 l 0 r n-1 while l ≤ r do m ( l + r) / 2 if key = = A[m] return m else if key < A[m] r m-1 else l m+1 return -1 Analysis : ● Input size: Array size, n ● Basic operation: key comparison ● Depend on Best – Matching the key with the middle piece. Worst – Often a key is not identified or a key in the list. ● Let C(n) denote the number of times the fundamental operation is performed. Then one, then Cworst t(n)= Performance in worst case. Since the algorithm after each comparison is the issue is divided into half the size we have, ● Cworst (n) = Cworst (n/2) + 1 for n > 1 ● C(1) = 1 |
|
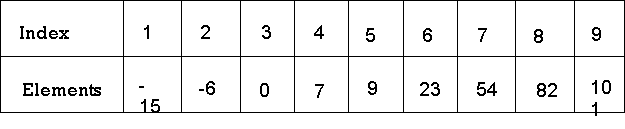
The number of comparisons required to check for various components is as follows: 1. Searching for x = 101 low high mid 1 9 5 6 9 7 8 9 8 9 9 9 Found Number of comparison : 4 2. Searching for x = 82 low high mid 1 9 5 6 9 7 8 9 8 Found Number of comparison : 3 3. Searching for x = 42 low high mid 1 9 5 6 9 7 6 6 6 7 6 not Found Number of comparison : 4 4. Searching for x = -14 low high mid 1 9 5 1 4 2 1 1 1 2 1 not Found Number of comparison : 3
|
 No part needs seeking more than 4 comparisons. Summarizing the
No part needs seeking more than 4 comparisons. Summarizing theComparisons were required for all nine things to be identified and divided by 9, yielding 25/9 . On average, there are around 2.77 comparisons per effective quest. Depending on the value of x, there are ten possible ways that an un-successful quest will end. If x < a[1], a[1] < x < a[2], a[2] < x < a[3], a[5] < x < a[6], a[6] < x < a[7] or a[7] < x < a[8] The algorithm requires 3 comparisons of components to decide the 'x' This isn't present. Binsrch needs 4 part comparisons for all of the remaining choices. Thus, the average number of comparisons of elements for a failed search is: (3 + 3 + 3 + 4 + 4 + 3 + 3 + 3 + 4 + 4) / 10 = 34/10 =3.4 The time complexity for a successful search is O(log n) and for an unsuccessful search is Θ(log n).
|