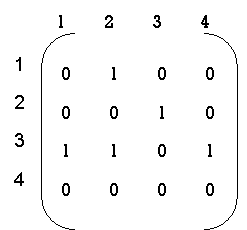
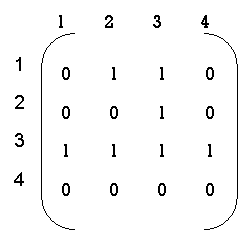
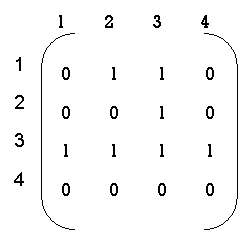
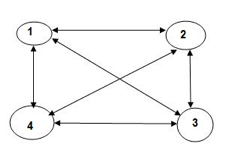
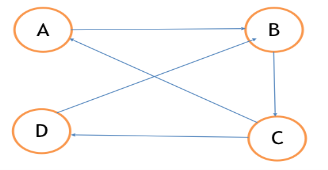
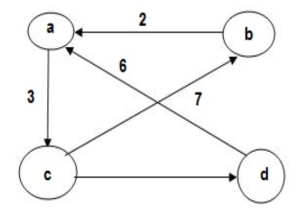
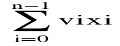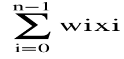● Warshall’s algorithm constructs transitive closure of given directd graph. ● In directed graph there are n vertices. ● Warshal’s construct the transitive closure through series of matrices R0,R1,R2,….Rn and matrices order will be n*n. ● Rn become required transitive closure. ● Vertices are numbered from 1 to n. ● So the closure matrices series start from R0 then equation become ● R k[i,j]=R (k-1) [i,j] |
Algorithm Warshall(A[1..n, 1..n]) // Computes transitive closure matrix // Input: Adjacency matrix A // Output: Transitive closure matrix R R(0) A for k→1 to n do for i→ 1 to n do for j→ 1 to n do R(k)[i, j] → R(k-1)[i, j] OR (R(k-1)[i, k] AND R(k-1)[k, j] ) return R(n) ● Directed Graph : A graph with each edge directed is called a directed OR digraph graph. ● Adjacency matrix : The adjacency matrix of a directed graph A = {aij} is the boolean matrix that has a directed graph. ● 1 - if from ith vertex to the jth vertex there is a directed edge. ● 0 - Otherwise ● Transitive Closure : It is possible to define the transitive closure of a directed graph with n vertices as the n-by-n matrix T={tij}, in which the elements in the ith row (1≤ I ≤ n) and the jth column (1 ≤ j ≤ n) are 1 if there is a nontrivial directed path (i.e. a positive length directed path) from the ith vertex to the jth vertex, otherwise tij is 0. The transitive closure provides data about a digraph with reach capability.
|
|
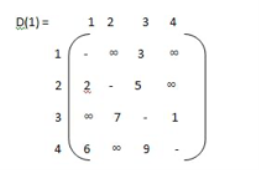
Now, R(1) [i.j].R(0)[i,j] or (R(0)[i,1] & R(0) [1,j]) step 1 :- 1st row --> 2 (element at place 2 ) 1st col --> 3 (element at place 3 ) now R = {3,2} R (1) = |
|
|
|
Given S ⊆ V with 1 ∈ S and given j ≠1, j ∈ S, let C(S, j) be the shortest path that starting at 1, visits all nodes in S and ends at j. Notice: • If |S| = 2, then C(S, k) = d1,k for k = 2, 3, . . . , n • If |S| > 2, then C(S, k) = the optimal tour from 1 to m, +dm,k, ∃m ∈ S − {k} Recursive definition of the optimal solution C(S, k) = d1, m if S = {1, k} min m≠k, m∈S[C(S − {k},m) + d(m, k)] otherwise ● In travelling salesman problem start with source node travel all the nodes once and come back to the starting node and which path gives the minimum cost for travelling that becomes the optimal solution for travelling salesman problem. ● Formula: ● G(i,s)=min{Cik+ G( k, S- { k } )} TSP Algorithm. g (i,s) = min kϵs [Cik + g ( K , S – {K})] |
|
|
|
|
|
|
|
f(i,w) = 0 if i = −1 and 0 ≤ w ≤ c −∞ if i = −1 and w < 0 max {xivi + f(i − 1, w − xiwi)} if i ≥ 0 xi∈{0,1}
|
D = D(i,w) = _{0} if wi > w {0, 1} if wi ≤ w |
f(i,w) = 0 if i = −1 and 0 ≤ w ≤ c max {xivi + f(i − 1, w − xiwi)} if i ≥ 0 xi∈D
|
value | weight | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
4 | 3 | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
5 | 4 | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
7 | 5 | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
|
|
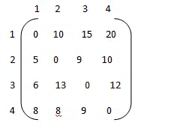
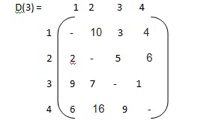
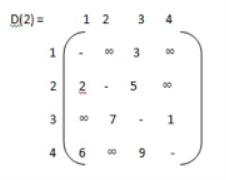
Algorithm Floyd(W[1..n, 1..n]) // Implements Floyd‘s algorithm // Input: Weight matrix W // Output: Distance matrix of shortest paths‘ length D W for k → 1 to n do for i→ 1 to n do for j→ 1 to n do D [ i, j] → min { D [ i, j], D [ i, k] + D [ k, j] return D
|
|
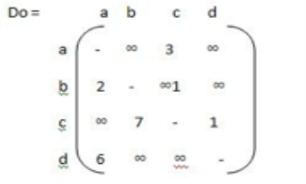
Step 1: construction of matrix. Do if i = j then wij = ‘ - ‘ else if i - - - > j = { c } else matrix ∞ |
|
|
|