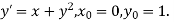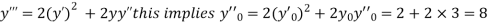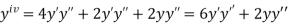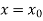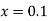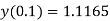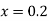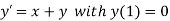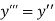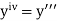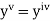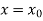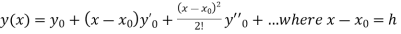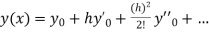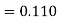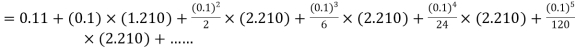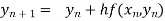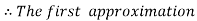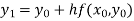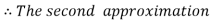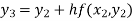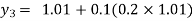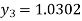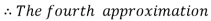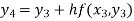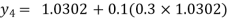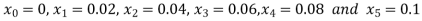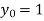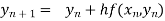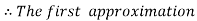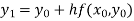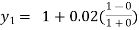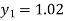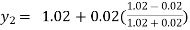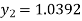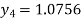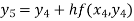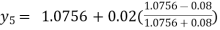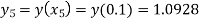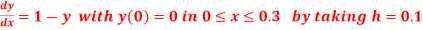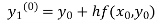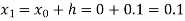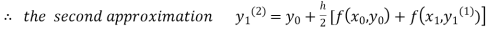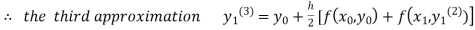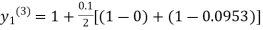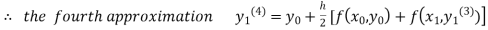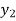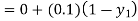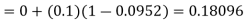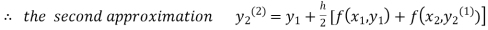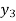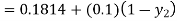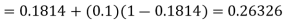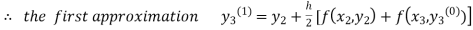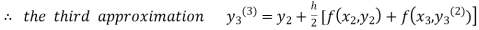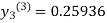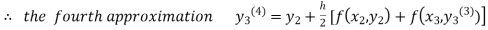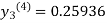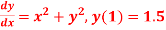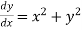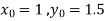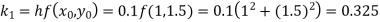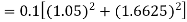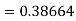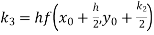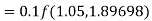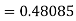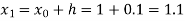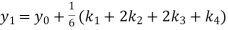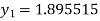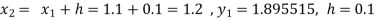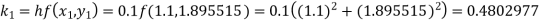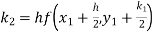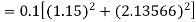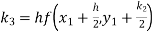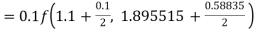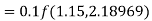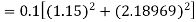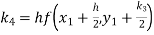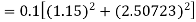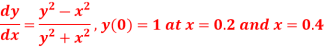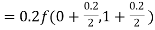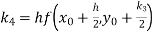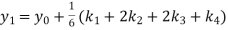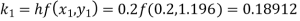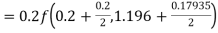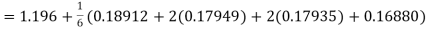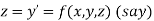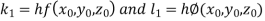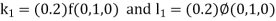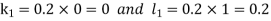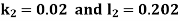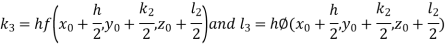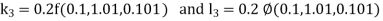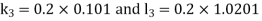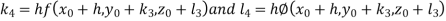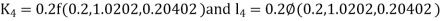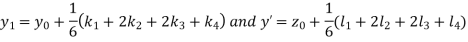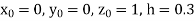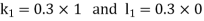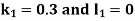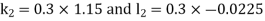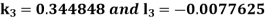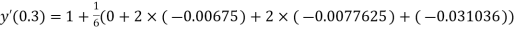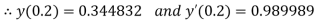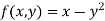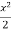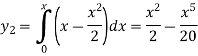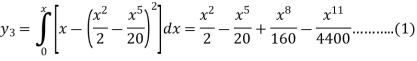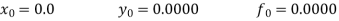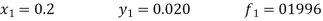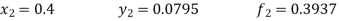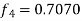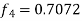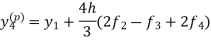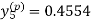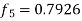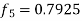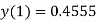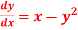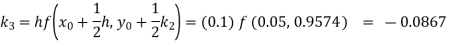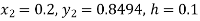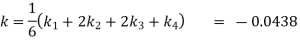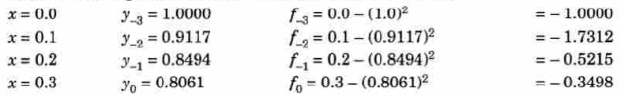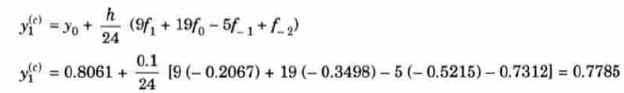undefined | unit 1 numerical methods - Goseeko

Back to Study material

EM-IV

Unit-1Numerical methodsQ1) Solve

,

using Taylor’s series method and compute

.A1)

Here This implies that .

Differentiating, we get

.

.

.

The Taylor’s series at ,

(1)

At in equation (1) we get

At in equation (1) we get

Q2) Solve

numerically, start from

and carry to

using Taylor’s series method.A2)

Here .

We have

Differentiating, we get

implies that or

implies that or .

implies that

implies that

The Taylor’s series at ,

Or

Here

The Taylor’s series

.

Q3) Use Euler’s method to find y(0.4) from the differential equation

with h=0.1

A3)

Given equation

Here

We break the interval in four steps.

So that

By Euler’s formula

, n=0,1,2,3 ……(i)

For n=0 in equation (i) we get

For n=1 in equation (i) we get

.01

For n=2 in equation (i) we get

For n=3 in equation (i) we get

Hence y(0.4) =1.061106.

Q4) Given

with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method (five steps).A4)

Given equation is

Here

No. of steps n=5 and so that

So that

Also

By Euler’s formula

, n=0,1,2,3,4 ……(i)

For n=0 in equation (i) we get

For n=1 in equation (i) we get

For n=2 in equation (i) we get

For n=3 in equation (i) we get

For n=4 in equation (i) we get

Hence

Q5) Using modified Euler’s method, obtain a solution of the equation

A5)Given

equation

Here

By modified Euler’s formula the initial iteration is

The iteration formula by modified Euler’s method is

-----(i)

For n=0 in equation (i) we get

Where and as above

For n=1 in equation (i) we get

For n=2 in equation (i) we get

For n=3 in equation (i) we get

Since third and fourth approximation are equal.

Hence y=0.0952 at x=0.1

To calculate the value of at x=0.2

By modified Euler’s formula the initial iteration is

The iteration formula by modified Euler’s method is

-----(ii)

For n=0 in equation (ii) we get

1814

For n=1 in equation (ii) we get

1814

Since first and second approximation are equal.

Hence y = 0.1814 at x=0.2

To calculate the value of at x=0.3

By modified Euler’s formula the initial iteration is

The iteration formula by modified Euler’s method is

-----(iii)

For n=0 in equation (iii) we get

For n=1 in equation (iii) we get

For n=2 in equation (iii) we get

For n=3 in equation (iii) we get

Since third and fourth approximation are same.

Hence y = 0.25936 at x = 0.3

Q6) Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that

A6)Given

equation

Here

Also

By Runge Kutta formula for first interval

Again

A fourth order Runge Kutta formula:

To find y at

A fourth order Runge Kutta formula:

Q7) Using Runge Kutta method of fourth order, solve

A7)Given

equation

Here

Also

By Runge Kutta formula for first interval

)

A fourth order Runge Kutta formula:

Hence at x = 0.2 then y = 1.196

To find the value of y at x=0.4. In this case

A fourth order Runge Kutta formula:

Hence at x = 0.4 then y=1.37527

Q8) Using RungeKutta method of order four , solve

to find

A8)

Given second order differential equation is

Let then above equation reduces to

Or

(say)

Or .

By RungeKutta Method we have

A fourth orderRungeKutta formula:

Q9: Solve the differential equations

for

Using four order Runge Kutta method with initial conditions

A9)

Given differential equation are

Let

And

Also

By RungeKutta Method we have

A fourth orderRungeKutta formula:

And

.

Q10) Find the solution of the differential equation

in the range

for the boundary conditions y = 0 and x = 0 by using Milne’s method.A10)By using Picards method-

Where

To get the first approximation-

We put y = 0 in f(x, y),

Giving-

In order to find the second approximation, we put y = in f(x,y)

Giving-

And the third approximation-

Now determine the starting values of the Milne’s method from equation (1), by choosing h = 0.2

Now using the predictor-

X = 0.8

,

And the corrector-

, ................(2)

Now again using corrector-

Using predictor-

X = 1.0,

,

And the corrector-

,

Again using corrector-

, which is same as before

Hence

Q11) Solve the intital value problem

, y(0) = 1

to find y(0.4) by using Adams-Bashforth method. Starting solutions required are to be obtained using Runge-Kutta method of order 4 using step value h = 0.1A11)

Here we have-

Here

So that-

Thus

To find y(0.2)-

Here

Thus,

Y(0.2) =

To find y(0.3)-

Here

Thus,

Y(0.3) =

Now the starting values of Adam’s method with h = 0.1-

Using predictor-

Using corrector-

Hence