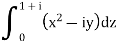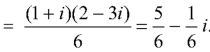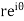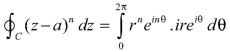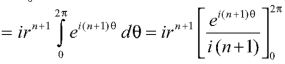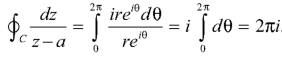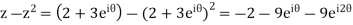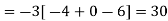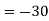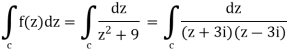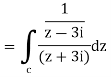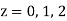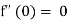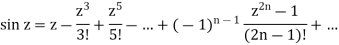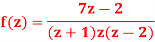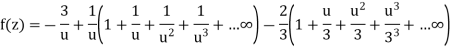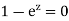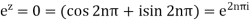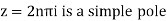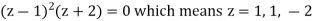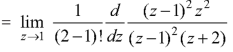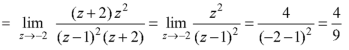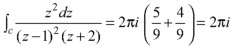|
Along the line y = x, dy = dx that dz = dx + i dy dz = dx + i dx = (1 + i) dx
On putting y = x and dz = (1 + i)dx
|
|
The equation of a circle C is |z - a| = r or z – a = Where dz =
Which is the required value. When n = -1
|
|
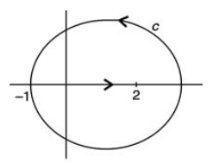
The equation of the circle is-
Or
Now for the lower semi-circle-
|
|
Here we have-
Hence the poles of f(z),
Note- put determine equal to zero to find the poles.
Here pole z = -3i lies in the given circle C. So that-
|
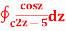 where C =
where C = 
A5)
= =
|
|
Here we have-
Find its poles by equating denominator equals to zero.
We get-
There are two poles in the circle- Z = 0 and z = 1 So that-
|
It is given that-
Now-
We know that, Taylor’s series-
So that
Hence
|
|
Let z + 1 = u, we get-
Here since 1 < u < 3 or 1/u < 1 and u/3 < 1, Now expanding by Binomial theorem-
Hence
Which is valid in the region 1 < z + 1 < 3 |
|
Here we have-
We find the poles by putting the denominator equals to zero. That means-
|
|
|
The poles of the function are-
The pole at z = 1 is of second order and the pole at z = -2 is simple- Residue of f(z) (at z = 1)
Residue of f(z) ( at z = -2)
|