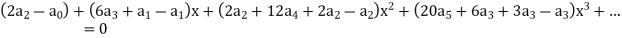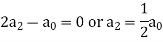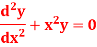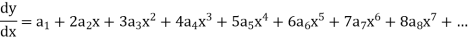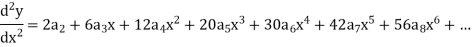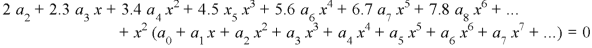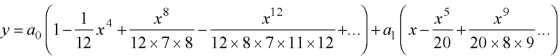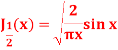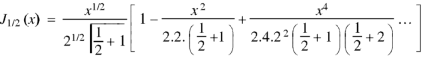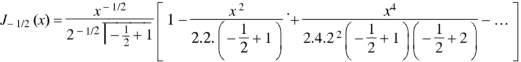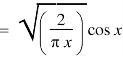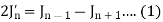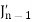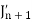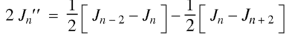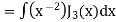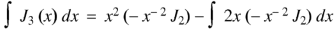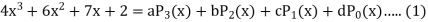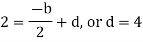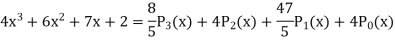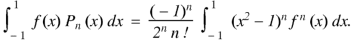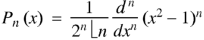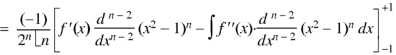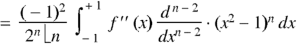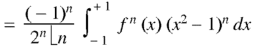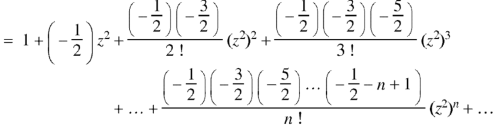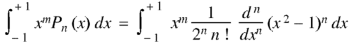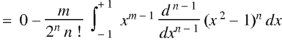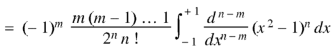|
Here we have-
Let the solution of the given differential equation be-
Since x = 0 is the ordinary point of the given equation-
Put these values in the given differential equation-
Equating the coefficients of various powers of x to zero, we get-
Therefore, the solution is-
|
|
Here we have-
Let us suppose-
Since x = 0 is the ordinary point of (1)- Then-
And
Put these values in equation (1)- We get-
Equating to zero the coefficients of the various powers of x, we get-
And so on…. In general, we can write-
Now putting n = 5,
Put n = 6-
Put n = 7,
Put n = 8,
Put n = 9,
Put n = 10,
Put the above values in equation (1), we get-
|
|
As we know that-
Now put n = 1/2 in equation (1), then we get-
Hence proved. |
|
Put n = -1/2 in equation (1) of the above question, we get-
|
|
We know that- The recurrence formula-
On differentiating, we get-
Now replace n by n -1 and n by n+1 in (1), we have-
Put the values of
|
|
We know that- from recurrence formula
On integrating we get-
On taking n = 2 in (1), we get-
Again-
Put the value of
By equation (1), when n = 1
|
 in terms of Legendre polynomials.A7)
in terms of Legendre polynomials.A7)
By equating the coefficients of like powers of x, we get-
Put these values in equation (1), we get-
|
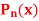 be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
|
We know that-
On integrating by parts, we get-
Now integrate (n – 2) times by parts, we get-
|
|
We know that
Equating the coefficients of
|
|
By using Rodrigue formula for Legendre function.
On integrating by parts, we get-
Now integrating m – 2 times, we get-
|