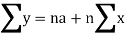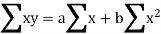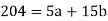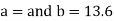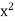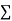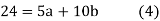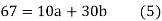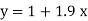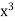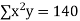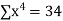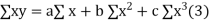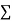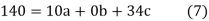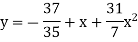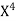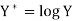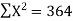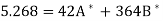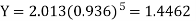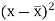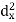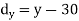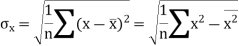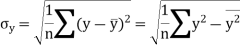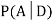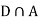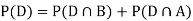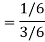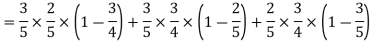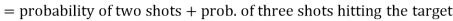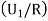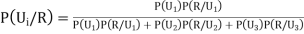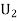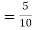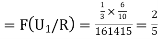undefined | unit 5 statistical methods

EM-IV

Unit 5Statistical methodsQ1) Find the straight line that best fits of the following data by using method of least square.

X	1	2	3	4	5
y	14	27	40	55	68

A1)Suppose the straight line y = a + bx…….. (1) Fits the best-Then-

x	y	xy
1	14	14	1
2	27	54	4
3	40	120	9
4	55	220	16
5	68	340	25
Sum = 15	204	748	55

Normal equations are-

Put the values from the table, we get two normal equations-

On solving the above equations, we get-

So that the best fit line will be- (on putting the values of a and b in equation (1))

Q2) Find the best values of a and b so that y = a + bx fits the data given in the table

x	0	1	2	3	4
y	1.0	2.9	4.8	6.7	8.6

A2) y = a + bx

x	y	xy
0	1.0	0	0
1	2.9	2.0	1
2	4.8	9.6	4
3	6.7	20.1	9
4	8.6	13.4	16
x = 10	y ,= 24.0	xy = 67.0

Normal equations, y= na+ bx (2)

On putting the values of

On solving (4) and (5) we get,

On substituting the values of a and b in (1) we get

Q3) Find the least squares approximation of second degree for the discrete data

x	2	-1	0	1	2
y	15	1	1	3	19

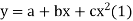
A3)Let the equation of second-degree polynomial be

x	y	xy
-2	15	-30	4	60	-8	16
-1	1	-1	1	1	-1	1
0	1	0	0	0	0	0
1	3	3	1	3	1	1
2	19	38	4	76	8	16
x=0	y=39	xy=10

Normal equations are

On putting the values of x, y, xy, have

On solving (5),(6),(7), we get,

The required polynomial of second degree is

Q4) Fit a second-degree parabola to the following data.

X = 1.0	1.5	2.0	2.5	3.0	3.5	4.0
Y = 1.1	1.3	1.6	2.0	2.7	3.4	4.1

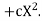A4)We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.Let the parabola of fit be y = a + bX

The values of

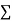X etc. Are calculated as below:

x	X	y	Xy
1.0	-3	1.1	-3.3	9	9.9	-27	81
1.5	-2	1.3	-2.6	4	5.2	-5	16
2.0	-1	1.6	-1.6	1	1.6	-1	1
2.5	0	2.0	0.0	0	0.0	0	0
3.0	1	2.7	2.7	1	2.7	1	1
3.5	2	3.4	6.8	4	13.6	8	16
4.0	3	4.1	12.3	9	36.9	27	81
Total	0	16.2	14.3	28	69.9	0	196

The normal equations are

7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9

Solving these as simultaneous equations we get

Replacing X bye 2x – 5 in the above equation we get

Which simplifies to y =

This is the required parabola of the best fit.

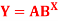Q5) Estimate the chlorine residual in a swimming pool 5 hours after it has been treated with chemicals by fitting an exponential curve of the form

of the data given below-

Hours(X)	2	4	6	8	10	12
Chlorine residuals (Y)	1.8	1.5	1.4	1.1	1.1	0.9

A5)

Taking log on the curve which is non-linear,

We get-

Put

Then-

Which is the linear equation in X,

Its normal equations are-

Here N = 6,

Thus the normal equations are-

On solving, we get

A = 2.013 and B = 0.936

Hence the required least square exponential curve-

Prediction-

Chlorine content after 5 hours-

Q6) Find the correlation coefficient between Age and weight of the following data-

Age	30	44	45	43	34	44
Weight	56	55	60	64	62	63

A6)

x	y					())
30	56	-10	100	-4	16	40
44	55	4	16	-5	25	-20
45	60	5	25	0	0	0
43	64	3	9	4	16	12
34	62	-6	36	2	4	-12
44	63	4	16	3	9	12
Sum= 240	360	0	202	0	70	32

Karl Pearson’s coefficient of correlation-

Q7) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-

X	10	20	30	40	50
Y	90	85	80	60	45

A7)

X	Y
10	90	-20	400	20	400	-400
20	85	-10	100	15	225	-150
30	80	0	0	10	100	0
40	60	10	100	-10	100	-100
50	45	20	400	-25	625	-500
Sum = 150	360	0	1000	10	1450	-1150

Short-cut method to calculate correlation coefficient-

Q8) Compute the Spearman’s rank correlation coefficient of the dataset given below-

Person	A	B	C	D	E	F	G	H	I	J
Rank in test-1	9	10	6	5	7	2	4	8	1	3
Rank in test-2	1	2	3	4	5	6	7	8	9	10

A8)

Person	Rank in test-1	Rank in test-2	d =
A	9	1	8	64
B	10	2	8	64
C	6	3	3	9
D	5	4	1	1
E	7	5	2	4
F	2	6	-4	16
G	4	7	-3	9
H	8	8	0	0
I	1	9	-8	64
J	3	10	-7	49
Sum				280

Q9) Two variables X and Y are given in the dataset below, find the two lines of regression.

x	65	66	67	67	68	69	70	71
y	66	68	65	69	74	73	72	70

A9)

The two lines of regression can be expressed as-

And

x	y			xy
65	66	4225	4356	4290
66	68	4356	4624	4488
67	65	4489	4225	4355
67	69	4489	4761	4623
68	74	4624	5476	5032
69	73	4761	5329	5037
70	72	4900	5184	5040
71	70	5041	4900	4970
Sum = 543	557	36885	38855	37835

Now-

And

Standard deviation of x-

Similarly-

Correlation coefficient-

Put these values in regression line equation, we get

Regression line y on x-

Regression line x on y-

Q10) A box contains 4 white and 2 black balls and a second box contains three balls of each colour. Now a bag is selected at random and a ball is drawn randomly from the chosen box. Then what will be the probability that the ball is white.A10)Here we have two mutually exclusive cases-1. The first bag is chosen 2. The second bag is chosenThe chance of choosing the first bag is 1/2. And if this bag is chosen then the probability of drawing a white ball is 4/6.

So that the probability of drawing a white ball from first bag is-

And the probability of drawing a white ball from second bag is-

Here the events are mutually exclusive, then the required probability is-

Q11) A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.A11)

We consider the following events:

A: Selected item comes from A.

B: Selected item comes from B.

D: Selected item is defective.

We are looking for . We know:

Now,

So we need

Since, D is the union of the mutually exclusive events and (the entire sample space is the union of the mutually exclusive events A and B)

Q12) A die is rolled. If the outcome is a number greater than three. What is the probability that it is a prime number?A1)

The sample space is- S = {1, 2, 3, 4, 5, 6}

Let A be the event that the outcome is a number which is greater than three and B be the event that it is a prime.

So that-

A = {4, 5, 6} and B = {2, 3, 5} and hence

P(A) = 3/6, P(B) = 3/6 and

Now the required probability-

Q13) A can hit a target 3 times in 5 shots, B 2 times in 5 shots and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.What is the probability that-1. Two shots hit2. At least two shots hitA13)

1. Now probability that 2 shots hit the target-

Probability of at least two shots hitting the target

Q14) Three urns contains 6 red, 4 black, 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. lf the ball drawn is red find the probability that it is drawn from the first urn.A14)

Let: the ball is drawn from urn 1.