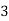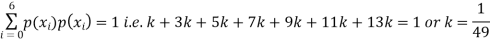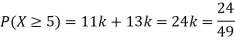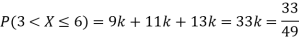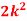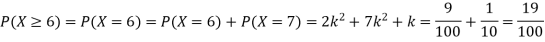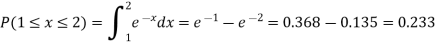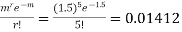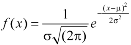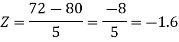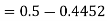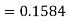undefined | unit 6 random variables

EM-IV

Unit 6Random variablesQ1) Find the probability distribution of the number of heads when three coins are tossed simultaneously.A1)Let be the number of heads in the toss of three coins

The sample space will be-

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Here variable X can take the values 0, 1, 2, 3 with the following probabilities-

P[X= 0] = P[TTT] = 1/8

P[X = 1] = P [HTT, THH, TTH] = 3/8

P[X = 2] = P[HHT, HTH, THH] = 3/8

P[X = 3] = P[HHH] = 1/8

Hence the probability distribution of X will be-

X
P(x)

Q2) For the following probability distribution of a discrete random variable X,

Find-1. The value of c.2. P[1<x<4]A2)

1. We know that-

So that-

0 + c + c + 2c + 3c + c = 1

8c = 1

Then c = 1/8

Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8

Q3) The probability density function of a variable X is

X	0	1	2	3	4	5	6
P(X)	k	3k	5k	7k	9k	11k	13k

(i) Find

(ii) What will be e minimum value of k so that

A3)

(i) If X is a random variable then

(i) Thus minimum value of k=1/30.

Q4) A random variate X has the following probability function

x	0	1	2	3	4	5	6	7
P (x)	0	k	2k	2k	3k

(i) Find the value of the k.(ii)

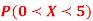A4)

(i) If X is a random variable then

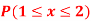Q5: Show that the following function can be defined as a density function and then find

A5)

here

So that, the function can be defined as a density function.

Now.

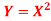Q6) Let X be a continuous random variable with PDF given by

, find the CDF of Y.A6)

First we note that , we have

Thus,

Q7) The probability that a man aged 60 will live to be 70 is 0.65. what is the probability that out of 10 men, now 60, at least seven will live to be 70?A7)

The probability that a man aged 60 will live to be 70

Number of men= n = 10

Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)

= P (7)+ P(8)+ P(9) + P(10) =

Q8) A die is tossed thrice. A success is getting 1 or 6 on a TOSS. Find the mean and variance of the number of successes.A8)

Q9) Suppose 3% of bolts made by a machine are defective, the defects occuring at random during production. If bolts are packaged 50 per box, find (a) Exact probability and(b) Poisson approximation to it, that a given box will contain 5 defectives.A9)

(a) Hence the probability for 5 defectives bolts in a lot of 50.

(b) To get Poisson approximation m = np =

Required Poisson approximation=

Q10) 1. If X

then find the probability density function of X.2. If X

then find the probability density function of X.A10)

1. We are given X

Here

We know that-

Then the p.d.f. will be-

2. . We are given X

Here

We know that-

Then the p.d.f. will be-

Q11) If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-1. P[X > 95] 2. P[X < 72]3. P [85 < X <97] [Note- use the table- area under the normal curve]A11)

The standard normal variate is –

Now-

1. X = 95,

So that-

2. X = 72,

So that-

3. X = 85,

X = 97,

So that-

Q12) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed.A12)

Here-

And

Area for non-defective washers = area between z = -1.2 to +1.2

= 2 area between z = 0 and z = 1.2

= 2 × 0.3849 = 0.7698 = 76.98%

Then percent of defective washers = 100 – 76.98 = 23.02 %

Sign Up