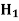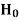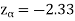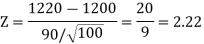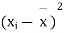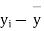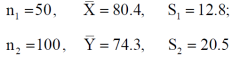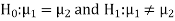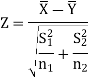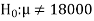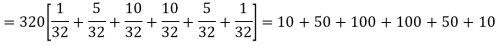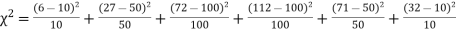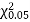undefined | unit 7 sampling

EM-IV

Unit 7SamplingQ1) Define type-1 and type-2 errors.A1)Type-1 and Type-2 error-Type-1 error-The decision relating to rejection of null hypo. When it is true is called type-1 error.The probability of type-1 error is called size of the test, it is denoted by

and defined as-

Note-

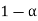is the probability of correct decision.Type-2 error-The decision relating to non-rejection of null hypo. When it is false is called type-1 error.It is denoted by

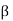and defined as-

Decision	true	true
Reject	Type-1 error	Correct decision
Do not reject	Correct decision	Type-2 error

Q2) define one tailed and two tailed tests.A2)One tailed and two tailed tests-A test of testing the null hypothesis is said to be two-tailed test if the alternative hypothesis is two-tailed whereas if the alternative hypothesis is one-tailed then a test of testing the null hypothesis is said to be one-tailed test.For example, if our null and alternative hypothesis are-

then the test for testing the null hypothesis is two-tailed test because the alternative hypothesis is two-tailed.If the null and alternative hypotheses are-

then the test for testing the null hypothesis is right-tailed test because the alternative hypothesis is right-tailed.Similarly, if the null and alternative hypotheses are-

then the test for testing the null hypothesis is left-tailed test because the alternative hypothesis is left-tailed Q3) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?A3)It is given that-Specified value of population mean =

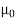= 460,Sample size = 100Sample mean = 453Sample standard deviation = S = 25

The null and alternative hypothesis will be-

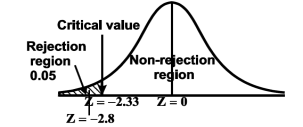
Also the alternative hypothesis left-tailed so that the test is left tailed test.

Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by

We get the critical value of left tailed Z test at 1% level of significance is

Since calculated value of test statistic Z (= ‒2.8) is less than the critical value

(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance

.Q4) A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with standard deviation 90 hours. Should the company accept the new brand at 5% level of significance?A4)Here we have-

The company may accept the new CFL light when average life ofCFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is

> 1200 and its complement is

≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,

Since the alternative hypothesis is right-tailed so the test is right-tailed test.Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for Z-test instead of t-test.Therefore, test statistic is given by

The critical values for right-tailed test at 5% level of significance is

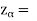1.645Since calculated value of test statistic Z (= 2.22) is greater than critical value (= 1.645), that means it lies in rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at 5% level of significanceThus, we conclude that sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs Q5) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?

Boys	1	2	3	4	5	6	7	8	9	10	11
Marks I test	23	20	19	21	18	20	18	17	23	16	19
Marks II test	24	19	22	18	20	22	20	20	23	20	17

A5) We compute the mean and the S.D. of the difference between the marks of the two tests as under:

Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.

Then

, nearly and df v=11-1=10
Students
1	23	24	1	0	0
2	20	19	-1	-2	4
3	19	22	3	2	4
4	21	18	-3	-4	16
5	18	20	2	1	1
6	20	22	2	1	1
7	18	20	2	1	1
8	17	20	3	2	4
9	23	23	-	-1	1
10	16	20	4	3	9
11	19	17	-2	-3	9

we find that

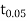(for v=10) =2.228. As the calculated value of

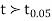, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching. Q6) From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight?A6) We calculate the means and standard derivations of the samples as follows

	Diet A			Diet B

10	-2	4	7	-8	64
6	-6	36	13	-2	4
16	4	16	22	7	49
17	5	25	15	0	0
13	1	1	12	-3	9
12	0	0	14	-1	1
8	-4	16	18	3	9
14	2	4	8	-7	49
15	3	9	21	6	36
9	-3	9	23	8	64
			10	-5	25
			17	2	4

120			180	0	314

Assuming that the samples do not differ in weight so far as the two diets are concerned i.e.

For v=20, we find =2.09

The calculated value of

Hence the difference between the samples means is not significant i.e. thew two diets do not differ significantly as regards their effects on increase in weight.

Q7) A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face-to-face mode yields examination results mean and SD respectively as-

and other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?A7)here we have-

Here we wish to test that both educational methods are statistically equal. If

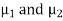denote the average marks of face to face and distance mode students respectively then our claim is

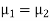and its complement is

≠

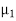. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

Since the alternative hypothesis is two-tailed so the test is two-tailed test.We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.For testing the null hypothesis, the test statistic Z is given by

The critical (tabulated) values for two-tailed test at 5% level of significance are-

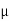Since calculated value of Z ( = 2.23) is greater than the critical values(= ±1.96), that means it lies in rejection region so wereject the null hypothesis i.e. we reject the claim at 5% level of significance Q8) A tube manufacturer claims that the average life of a particular categoryof his tube is 18000 km when used under normal driving conditions. A random sample of 16 tube was tested. The mean and SD of life of the tube in the sample were 20000 km and 6000 km respectively.Assuming that the life of the tube is normally distributed, test the claim of the manufacturer at 1% level of significance using appropriate test.A8)Here we have-

We want to test that manufacturer’s claim is true that the average life (

) of tube is 18000 km. So claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

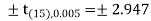Here, population SD is unknown and population under study is given to be normal.So here can use t-test-For testing the null hypothesis, the test statistic t is given by-

The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are

Since calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater that critical value (= − 2.947), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis. we conclude that sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true. Q9) A set of five similar coins is tossed 320 times and the result is

Number of heads	0	1	2	3	4	5
Frequency	6	27	72	112	71	32

A9)

For v = 5, we have

P, probability of getting a head=1/2;q, probability of getting a tail=1/2.

Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion

Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.

Hence,

Since the calculated value of is much greater than the hypothesis that the data follow the binomial law is rejected.

Q10) In experiments of pea breeding, the following frequencies of seeds were obtained

Round and yellow	Wrinkled and yellow	Round and green	Wrinkled and green	Total
316	101	108	32	556

Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.A10)

The corresponding frequencies are

Hence,

For v = 3, we have

Since the calculated value of is much less than there is a very high degree of agreement between theory and experiment.

Sign Up