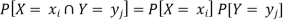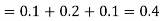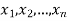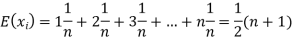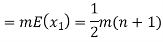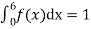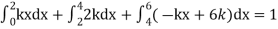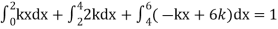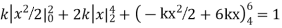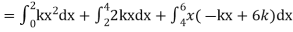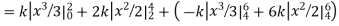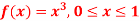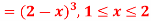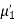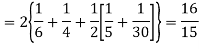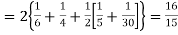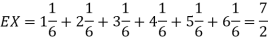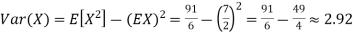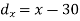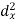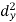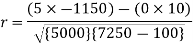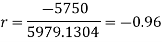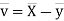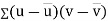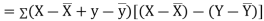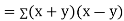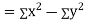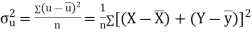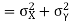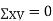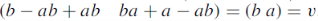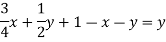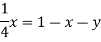Back to Study material
EM-IV

Unit-8Concept of joint probabilityQ1) Find the joint distribution of X andY, which are independent random variables with thefollowing respective distributions:

1

2

P [ X =

0.7

0.3

 And

-2

5

8

P [ Y =

0.3

0.5

0.2

A1)

Since X and Y are independent random variables,

Thus the entries of the joint distribution are the products

of the marginal entries

 

 

 Q2) The following table represents the joint probability distribution ofthe discrete random variable (X, Y):

X/Y

1

2

1

0.1

0.2

2

0.1

0.3

3

0.2

0.1

Then find-i) The marginal distributions.ii) The conditional distribution of X given Y = 1.iii) P[(X + Y) < 4].A2)i) The marginal distributions. 

X/Y

1

2

p(x) [totals]

1

0.1

0.2

0.3

2

0.1

0.3

0.4

3

0.2

0.1

0.3

p(y) [ totals]

0.4

0.6

1

 The marginal probability distribution of X is-

X

1

2

3

p(x)

0.3

0.4

0.3

 The marginal probability distribution of Y is 

Y

1

2

p(x)

0.4

0.6

 ii) The conditional distribution of X given Y = 1.

 

 

 

 The conditional distribution of X given Y = 1 is-

X

1

2

3

¼

1/4

½

  (iii) The values of (X, Y) which satisfy X + Y < 4 are (1, 1), (1, 2) and (2, 1)only.

Which gives-

  Q3) In a lottery, m tickets are drawn at a time out of a tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.A3)

Let be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have

Therefore expected value of the sum of the numbers on the tickets drawn

 Q4) X is a continuous random variable with probability density function given by

Find k and mean value of X.A4)

Since the total probability is unity.

Mean of X =

 

 Q5) The frequency distribution of a measurable characteristic varying between 0 and 2 is as under

Calculate two standard deviation and also the mean deviation about the mean.A5)

Total frequency N =

(about the origin)=

 

(about the origin)=

Hence,

i.e., standard deviation

Mean derivation about the mean

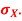 Q6) I roll a fair die and let X be the resulting number. Find E(X), Var(X), and A6)

We have   and for k = 1,2,…,6. Thus we have

Thus,

 Q7) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-

X

10

20

30

40

50

Y

90

85

80

60

45

A7)

X

Y

10

90

-20

400

20

400

-400

20

85

-10

100

15

225

-150

30

80

0

0

10

100

0

40

60

10

100

-10

100

-100

50

45

20

400

-25

625

-500

 

Sum = 150

 

360

 

0

 

1000

 

10

 

1450

 

-1150

 Short-cut method to calculate correlation coefficient-

 Q8) If X and Y are uncorrelated random variables, the of correlation between 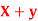and A8)

Let and

Then

Now

Similarly,

Now

Also

(As and are not correlated, we have )

Similarly,

 

 Q9) show that = (b a) is a fixed point of the stochastic matrix-

A9)

 

  Q10) Find the unique fixed probability vector t of

 

A10)

Suppose t = (x, y, z) be the fixed probability vector.

By definition x + y + z = 1. So t = (x, y,

1 − x − y), t is said to be fixed vector, if t P = t

On solving, we get-

Required fixed probability vector is-

 

  

Zoom Out
Zoom In
Sign Up
0 matching results found
Loading ....