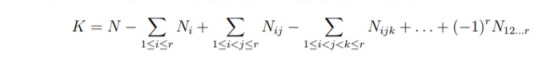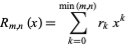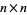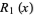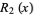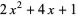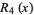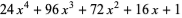GTC
UNIT – 6The Principle of Inclusion and Exclusion Q1) Write the Principle of Inclusion and Exclusion.A1)The Principal of Inclusion and Exclusion (PIE) theory is a counting technique which calculates the number of elements fulfilling at least one of several properties, while ensuring that elements satisfying more than one property are not counted twice. Generalised PIEOften the following theorem is called either the cross-classification theory, oror the principle of inclusion-exclusion. We are enunciating the principle now. Let S be a set of N distinct elements, and let S1, . . . , Sr be arbitrary subsets of S containing N1, . . . , Nr elements, respectively. For 1 ≤ i < j < . . . < l ≤ r, let Sij...l be the intersection of Si , Sj , . . . , Sl and let Nij...l be the number of elements of Sij...l. Then the number K of elements of S not in any of S1, . . . , Sr is
|
Q2) Explain Derangements – Nothing is in its Right PlaceA2) A Derangement is a permutation of n elements, so that in its original position, no element exists. For example, {0, 1, 2, 3} is a {2, 3, 1, 0} derangement. Q3) Find the total number of derangements of a group of n elements, given the number n.A3) Example 1 Input: n = 2Output: 1For two elements say {0, 1}, there is only one possible derangement {1, 0} Example 2Input: n = 3Output: 2For three elements say {0, 1, 2}, there are two possible derangements {2, 0, 1} and {1, 2, 0} Example 3Input: n = 4Output: 9For four elements say {0, 1, 2, 3}, there are 9possible derangements {1, 0, 3, 2} {1, 2, 3, 0}{1, 3, 0, 2}, {2, 3, 0, 1}, {2, 0, 3, 1}, {2, 3,1, 0}, {3, 0, 1, 2}, {3, 2, 0, 1} and {3, 2, 1, 0}
Q4) Explain Rook PolynomialA4) A rook polynomial is a generating polynomial in combinatorial mathematics for the number of ways to place non-attacking rooks on a board that looks like a checkerboard; that is, there may be no two rooks in the same row or column.
A rook polynomial is a polynomial
whose number of ways
where The first few rook polynomials
|
0 matching results found