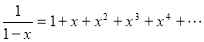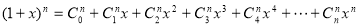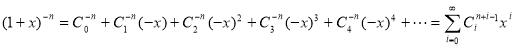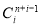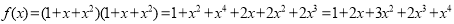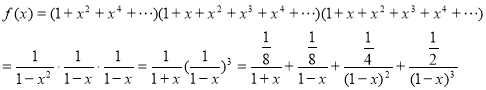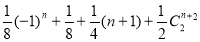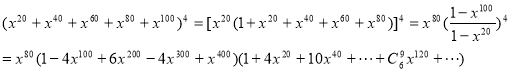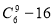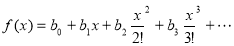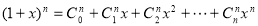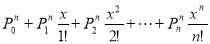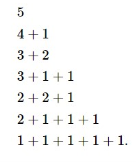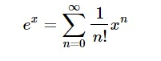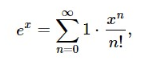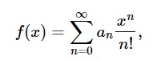Example 1.
Example 2.
Example 3.
Example 4.
|
(a) AA, AB or BA, BB: 3 ways. (b) AAB or BAA or ABA, BBA or BAB or ABB: 2 ways Utilizing the general generating function:
Q3) There are infinite A’s, B’s, and C’s. In how many ways can we select n letters from A’s, B’s, and C’s, with even numbers of A’s?
an=
Q4) There are 200 identical chairs. In how many ways can we place 4 rooms to have 20, or 40, or 60, or 80, or 100 chairs in each room? a200= |
Example. |
|
There are other ways that a function might be said to generate a sequence, other than as what we have called a generating function. For example,
is the generating function for the sequence 1,1,12,13!,…1,1,12,13!,…. But if we write the sum as
considering the n!n! to be part of the expression xn/n!xn/n!, we might think of this same function as generating the sequence 1,1,1,…1,1,1,…, interpreting 1 as the coefficient of xn/n!xn/n!. This is not a very interesting sequence, of course, but this idea can often prove fruitful. If
we say that f(x)f(x) is the exponential generating function for a0, a1, a2, … |