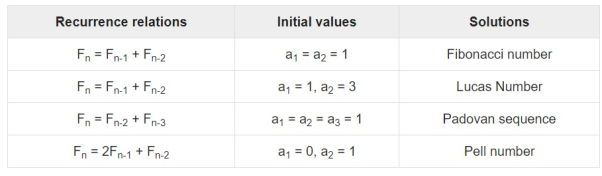
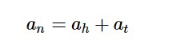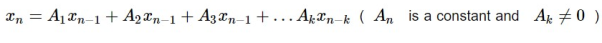 on a sequence of numbers as a first-degree polynomial.Examples:
on a sequence of numbers as a first-degree polynomial.Examples:
|
A relationship of recurrence is considered non-homogeneous if it is in the form of
Its associated homogeneous recurrence relation is Its associated homogeneous recurrence relation is
The solution (an)of a non-homogeneous recurrence relation has two parts. First part is the solution (ah)of the associated homogeneous recurrence relation and the second part is the particular solution (at).
The solution (an)of a non-homogeneous recurrence relation has two parts. First part is the solution (ah)of the associated homogeneous recurrence relation and the second part is the particular solution (at).
The first element of the approach is carried out using the protocols described in the previous section.
Let be the characteristic equation of the associated homogeneous recurrence relation and let x1 and x2 be its roots.
|
|