undefined | unit 2 block diagrams and signal flow graphs

Back to Study material

Unit-2Block Diagrams and Signal flow graphsQ1) What are poles and zeros of a transfer function?A1)

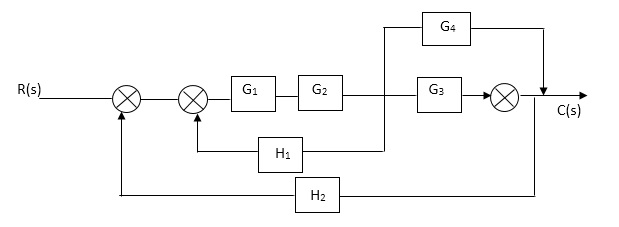
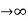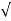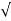The transfer function can be represented by the ratio of two polynomials

G (S) = a0sn+a1 sn-1-------+an/b0sm+b1sm-1+-----+bn

a0—an ---- constants

G(S) = K(s+z1) (s+z2) (as2+bs+c)/(S+A) (s+p2) (As2+Bs +c)

K= a0/b0 (Gain of system)

For poles –They are the values of s for which

G(S)

(S+p1)(S+p2)(A

S= p1, -p2 , -B±B2-4Ac/2A

For ZEROS – They are the values of s for which

G(S)

S=-z1, -z2 , -b±b2-4ac/2a

1)Location of poles and zeros in s place determines the reliability of the system 2) There can be multiple poles and zeros 3) The numerator of transfer function when equalized to zero gives zero of system4) The denominator of transfer function which equalized to zero gives poles of system.Q2) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?

A3)

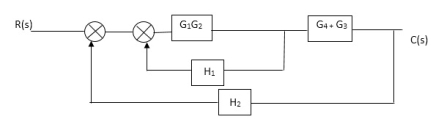
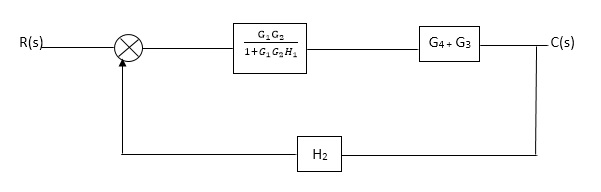
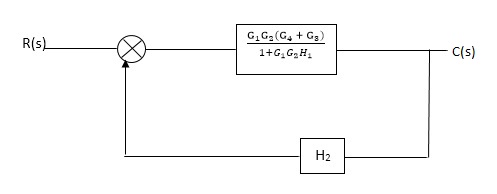
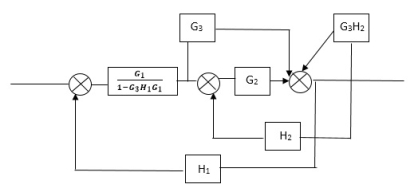
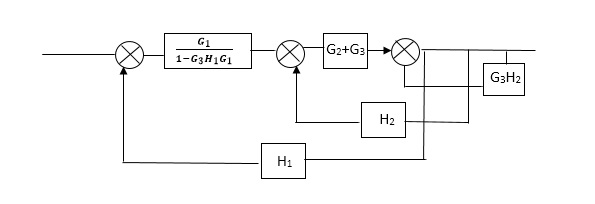
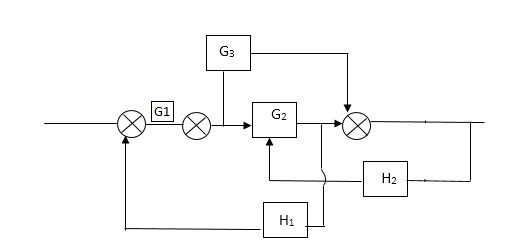
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1, G2(G3+G4) H2/1+G1G2H1

= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)

=G1G2(G3+G4)/1+(H1-H2) (G1G2) (G3+G4)

C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2

Q3) Reduce the Block diagram

A3)

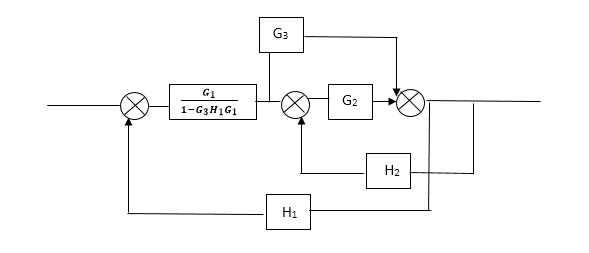
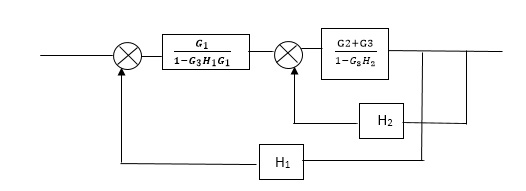
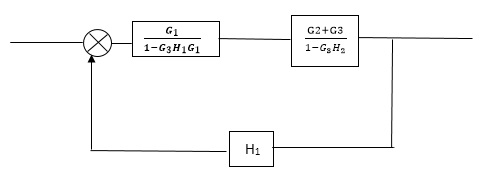
C(s)/R(s)= G1(G3+G2)/(1-G1G3X1) (1-G2X2) H1

= G(G3+G2)/(1-G3G1H1) (1-G2H2) + G1H1(G3+G2)

= G1(G3+G2)/1-G3G1H1-G2H2+G1H1(G3+G2H1

=G1(G3+G2)/1-G3H2+G1G2H1(1+G3H2)

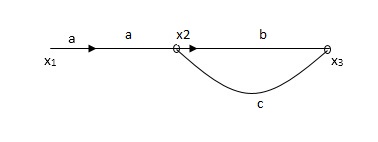
Q4) The SFG shown has forward path and singles iAnsated loop determine overall transmittance relating X3 and X1?

A4) X1- I/p node X2-Intenmediale node X3- o/p node ab- forward path (p) bc- 1 loop (L)At node XQ:X2 = x1a + x3c [Add i/p signals at node]At node x3: x2b =x3 (x1a+x3c) b = x3 X1ab = x3 (1-bc) X1 = x3 (1-bc)/ab Ab/(1-bc) = x3/x1 T= p/1-L

X1: - I/p node x2, x3, x4, x5, Qnlexmedili node

X0:- o/p node abdeg:- forward path

bc, ef :- Loop [iAnsated]

x2 = ax1+c x3

x3= bx2

x4 = d x3+f x5

x5 = e x4

x6= g x5

x6 = g (e x4) = ge [dx3+ e f x5]

xb = ge [d (bx2) + f (e x4)]

xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]

xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+

f(e [db (ax1+ cx3)

x2 = ax1 + cb (x2) x4 = d bx2 + f exq

x2 = ax1 + cbx2 = db (d4) + fe/1-cb

x2 = ax1/(1-cb) xy = db x2 + f x6/g

xy = db [ax1]/1-cb + f xb/g

x5 = c db (ax1)/1-cb + efxb/g

xb = gx5

= gedb (ax1)/1-cb + g efxb/g

Xb = gx5

gedb (ax1)/1-cb + g efxb/g

(1- gef/g) xb = gedb ax1/1-ab

Xb/x1 = gedb a/ (1- ef – bc + beef

Xb/x1 = p/ 1- (L1+L2) + L1 L2 for iAnsated loops

Sign Up