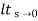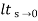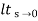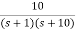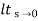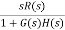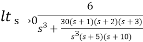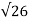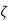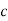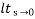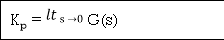C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1 C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST) C(S)/R(S) = K/S(1 + ST) + K C(S)/R(S) = K/T / S2 + S/T + K/T For second order system, S2 + 2ξWnS + Wn2 2ξWn = 1/T ξ = 1/2WnT Wn2 = K/T Wn =√K/T ξ = 1 / 2√K/T T ξ = 1 / 2 √KT forξ1 = 0.2, for ξ2 = 0.4 ξ1 = 1 / 2 √K1T ξ2 = 1 / 2 √K2T ξ1/ ξ2 = √K2/K1 K2/K1 = (0.2/0.4)2 K2/K1 = 1 / 4 K1 = 4K2 |
 . Find Kp, Kv and Ka?A5) Kp =
. Find Kp, Kv and Ka?A5) Kp = 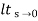 G(s)
G(s) T(s) = = 1 Kv = =
Ka = = = 0
|
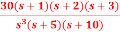 an input t3u(t) is applied. Find the steady state error?A6) ess=
an input t3u(t) is applied. Find the steady state error?A6) ess= 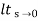
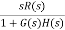 r(t) = t3u(t)R(s) = 6/s4H(s) =1
r(t) = t3u(t)R(s) = 6/s4H(s) =1ess= = = = 5/3 |
 . Determine the damping ratio, maximum overshoot, rise time?A7) The CLTF will be T(s) =
. Determine the damping ratio, maximum overshoot, rise time?A7) The CLTF will be T(s) = 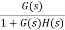
T(s) =
For second order system, S2 + 2ξWnS + Wn2 wn = 2ξWn = 5 i) Damping Ratio ii) Maximum overshoot Mp = e-∏ξ / √1 –ξ2 x 100 = e-∏x0.49 / √1 – (0.49)2 = 17.1% iii) Rise Time tr = ∏ - φ/Wd Wd = Wn√1 - ξ2 = 5.1 √1 – (0.49)2 = 4.45 sec φ= tan-1√1 – ξ2 / ξ = 1.059 rad tr = ∏ - φ/Wd = ∏ - 1.059/4.45 =468.53msec
|
 wnt/
wnt/ 1-
1- 2 sin (wdt+ø)Sin (wd +ø) = 0Wdt +ø = n
2 sin (wdt+ø)Sin (wd +ø) = 0Wdt +ø = n tr =n
tr =n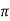 -ø/wdfor first time so, n=1.
-ø/wdfor first time so, n=1.
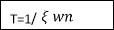 2) Peak Time (tp) The peak value attained by the output is called peak time. The time required by the output to reach this value is lp.d(cct) /dt = 0 (maxima)d(t)/dt = peak valuetp = n
2) Peak Time (tp) The peak value attained by the output is called peak time. The time required by the output to reach this value is lp.d(cct) /dt = 0 (maxima)d(t)/dt = peak valuetp = n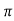 /wd for n=1tp =
/wd for n=1tp = 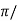 wd(3) Peak Overshoot Value Maximum deviation of output from steady state value is called peak overshoot value (Mp).
wd(3) Peak Overshoot Value Maximum deviation of output from steady state value is called peak overshoot value (Mp).Mp = e-∏ξ / √1 –ξ2 |
Condition 3 ξ = 1 C (S) = R (S) Wn2 / S2 + 2ξWnS + Wn2 C (S) = Wn2 / S (S2 + 2WnS + Wn2) [ R(S) = 1/S ] C (S) = Wn2 / S (S2 + Wn2) C (t) = 1 – e-Wnt + tWne-Wnt The response is critically damped. (4). Settling Time (ts): ts = 3 / ξWn (5%) ts = 4 / ξWn (2%) Q9) Determine the type and order of the system G(s)= K/S(S+1) G(S)= K(S+1)/S2(S+2) Sol: G(s)= K/S(S+1) It is order 2 and type 1 system G(S)= K(S+1)/S2(S+2) It is order 3 and type 2 system Q10) Derive position error coefficient? Sol: R(s)= Unit step R(t) = u(t) R(s) = 1/s ess = = ess=
(Position error coefficient)
|