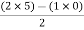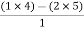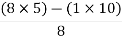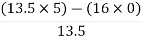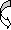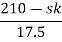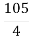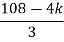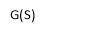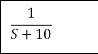For row S2 first term S2 = For row S2 Second term S2 = For row S1: S1 = For row S0 S0 = As there are two sign change in the first column, So there are two roots or right half of S-plane making system unstable.
|
Arrange in rows.
For row S2 first element S1 = Second terms = For S1 First element = For S0 First element = As there is no sign change for first column so all roots are is left half of S-plane and hence system is stable.
|
|
Special case II of Routh Hurwitz criterion forming auxiliary equation A1 (s) = 8S2 – 32 = 0
|
 find range of k for stabilityA4) Findlay characteristics equation.CE = 1+G (s) H(s) = 0H(s) =1 using feedbackCE = 1+ G(s)1+
find range of k for stabilityA4) Findlay characteristics equation.CE = 1+G (s) H(s) = 0H(s) =1 using feedbackCE = 1+ G(s)1+ 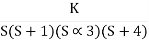 = 0S(S+1)(S+3)(S+4)+k = 0(S2+5)(S2+7Sα12)αK = 0S4α7S3α1252+S3α7S2α125αK = 0S4+8S3α19S2+125+k = 0
= 0S(S+1)(S+3)(S+4)+k = 0(S2+5)(S2+7Sα12)αK = 0S4α7S3α1252+S3α7S2α125αK = 0S4+8S3α19S2+125+k = 0By Routh Hurwitz Criterion
For system to be stable the range of K is 0< K <
|
| 1 | 12 | K |
S3 | 4 | 36 |
|
|
|
|
|
S2 | 3 | K |
|
S1 |
|
|
|
S0 | K |
|
|
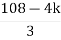 > 0 K < 27Range of K will be 0 < K < 27 Q6) Check if all roots of equation S3+6S2+25S+38 = 0, have real poll more negative than -1.A6)
> 0 K < 27Range of K will be 0 < K < 27 Q6) Check if all roots of equation S3+6S2+25S+38 = 0, have real poll more negative than -1.A6)S3 | 1 | 25 |
|
| 6 | 38 |
|
S1 | 18.67 |
|
|
S0 | 38 |
|
|
| 1 | 16 |
Z2 | 3 | 18 |
Z1 | 10 |
|
Z0 | 18 |
|
|
 .S = Z-S1After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane Q8) In detail explain the concept of stability?A8) A stable system always gives bounded output for bounded input and the system is known as BIBO stableA linear time invariant (LTI) system is stable if, The system is BIBO stableIn absence of the input the output tends towards zero
.S = Z-S1After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane Q8) In detail explain the concept of stability?A8) A stable system always gives bounded output for bounded input and the system is known as BIBO stableA linear time invariant (LTI) system is stable if, The system is BIBO stableIn absence of the input the output tends towards zero
|
[R(s) = 1]
C(t) = e-10t C(t)
|
 t= 0
t= 0 
 e-10t
e-10t  t
t e-10t C(t) 1
e-10t C(t) 1 1 0
1 0 tFig 5 BIBO stable figure
tFig 5 BIBO stable figure