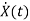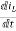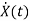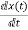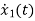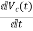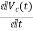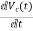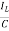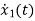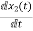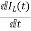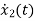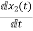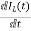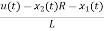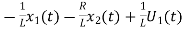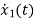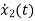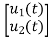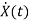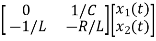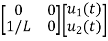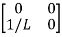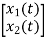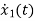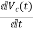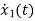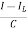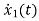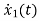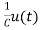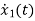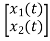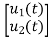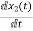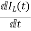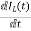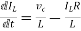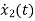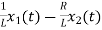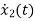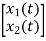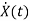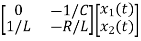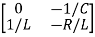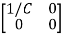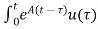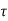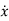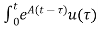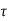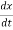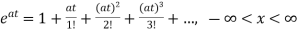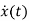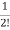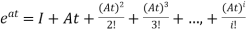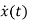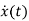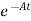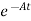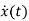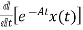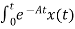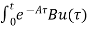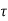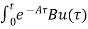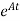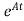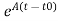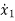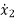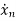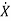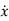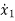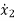|
|
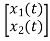 +[0]u(t)so, C=[1 0] D=[0]Now writing the state equation
+[0]u(t)so, C=[1 0] D=[0]Now writing the state equation
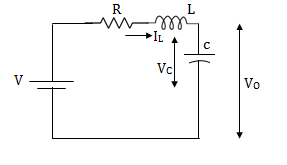
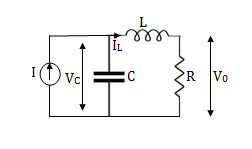
For that applying KVL in the above circuit V=ILR+L State Equation is
x1(t)=Vc
IL=C
VL=L
From KVL L
From equation (b) and (c)
Now writing the state equation
|
Hence A= |
|
|
V0=x2(t)R y(t)= V0= [0 R] The output equation is given as Y(t)=CX(t)+DU(t) C=[0 R] D=[0] Now finding state equation,we apply KCL in the given electrical circuit I=IC+IL
But I-IL=IC
|
Applying KVL in the given electrical circuit we get VC=VL+ILR VC-ILR=VL=L
From equation (b) and (c) we have Now writing the state equation
Hence A= |
Multiplying both sides by e-at x(t) = eat x(0) + Then for non-homogeneous state equation
The solution x(t) can be given as x(t) = eAt x(0) +
|
x(t)= Consider state equation
|
x(t)=a0+a1t+a2t2+a3t3+….+aiti substituting value in above equation a1+2a2t2+3a3t3+……….=A[a0+a1t+a2t2+a3t3+….+aiti] a1=Aa0 a2= ai= Solution for x(t) will be x(t)=[I+At+ The matrix exponential form can be written as
The solution x(t) will be x(t)=
Multiplying both sides by Integrating both sides w.r.t t we get
Multiplying both sides by x(t)=
At t=t0 x(t)= The above equation is the required solution |
|
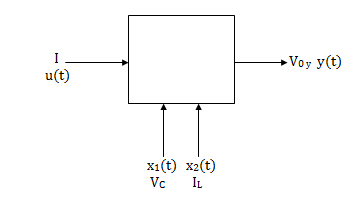
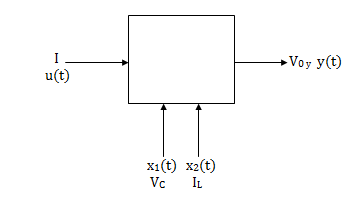
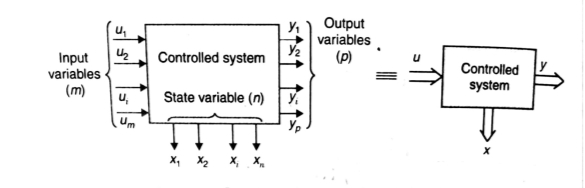
So, the above system shown can be described through equations as
The above set of equations can be represented as
As we are concerned for time invariant system, for which the term
The above equation can be represented in matrix form as given below |
 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)