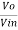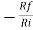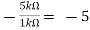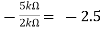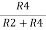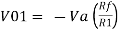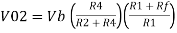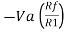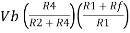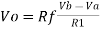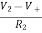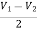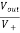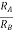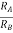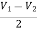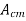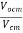|
R1 = 1KΩ Rf = 100KΩ V+ = 15V and V-=-15V. vi = 1V Af = -Rf/R1 = -100K/1K = -100 Af = vo/vi Vo = Af vi = -100 x 1V = -100V The output voltage cannot exceed the DC power supply voltage. Since vo is negative and large it is limited to V- Vo ≈ V- = -15V |
Peak to peak input voltage 2Vm = 200 mV Vm = 100 mV Vi= Vm sin wt = 100 sin wt mV Vo = -Rf/R1 x vi = -10 x 100 sinwt mV = -1000 sin wt mV |
Vo = Sum of all input voltages applied at both the terminals Vo = Va + Vb + Vc +Vd Vo = -3 -8 +9 +5 Vo = +3V |
|
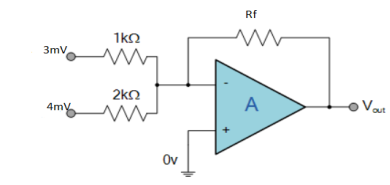
Gain (Av) = Hence, Av1 = Av2 = Now, Output voltage Vo = Sum of the two amplified input signals Vo = Av1 x V1 + Av2 x V2 Vo =(-5 x 3) + ( -2.5x 4) mV Vo = -25mV As the above output voltage is negative hence it is an inverting amplifier.
|
|
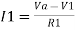
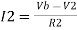
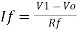
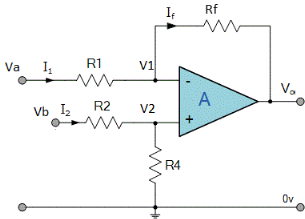
Summing point, V1 = V2 and V2 = Vb If Vb = 0 then And Va = 0 then Vo = -V01 + V02 Vo = If R1 = R2 and Rf = R4 then
And if R1 = R2 = Rf = R4 =R then Vo = Vb – Va
|
|
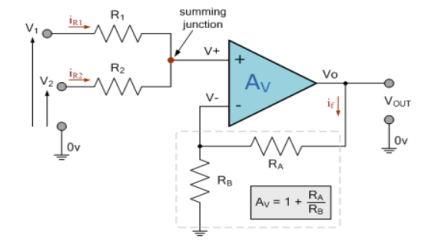
Applying KCL to the above circuit we have IR1+IR2 = 0
When R1 = R2 =R V+ = The voltage gain for non-inverting summing amplifier is given as AV = Vout/Vin = Vout= [1+ |
|
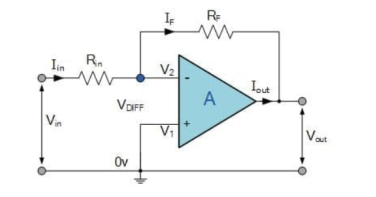
Due to high input impedance of Op-amp the current flowing into its inverting input terminal is zero. Therefore, the same current flows through R1 and Rf . i 1 = i f But i1 = vi – v1 / R1 = vi/R1 i f = v1 – vo / Rf = -vo/Rf vi/R1 = - vo/Rf Af = vo/vi = -Rf/R1 |
|
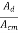
|
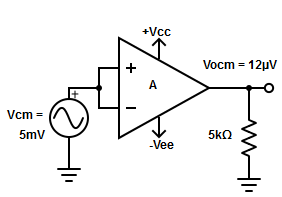
Where: Vocm = output common mode voltage Vcm = input common mode voltage Acm = common mode voltage gain In normal cases the value of Ad is large and Acm is very small making the value of CMRR very high.
|
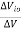
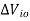 = Change in input offset voltage
= Change in input offset voltage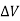 = Change in supply voltage
= Change in supply voltage