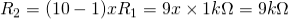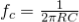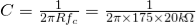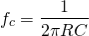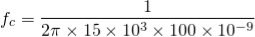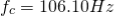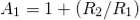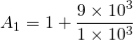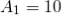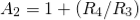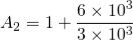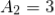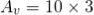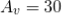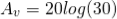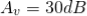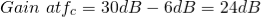UNIT6 | unit 6 non linear circuit applications

LICA

UNIT-6Non-Linear Circuits ApplicationsQ1) An Astable 555 Oscillator is constructed using the following components, R1 = 1kΩ, R2 = 2kΩ and capacitor C = 10uF. Calculate the output frequency from the 555 oscillator and the duty cycle of the output waveform.A1)

t1 – capacitor charge “ON” time is calculated as:

t1 = 0.693(R1 + R2). C

= 0.693(1000 +2000) x 10 x 10 -6 = 0.021 s= 0.21 msec

t2 – capacitor discharge “OFF” time is calculated as:

t2 = 0.693 R2. C

= 0.693 X 2000 x 10 x 10 -6 = 14ms

Total periodic time (T) is therefore calculated as:

T = t1 + t2 = 21 ms + 14 ms = 35 ms.

The output frequency, ƒ is therefore given as:

f = 1/T = 1/35ms = 28.6 Hz

Giving a duty cycle value of:

Duty Cycle = R1 + R2 / (R1 + 2 R2) = 1000 + 2000/ (1000 + 2 x 2000) = 60%

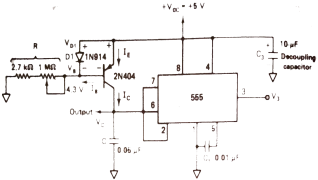
Q2) Compare a stable, monostable and bistable multivibrators?A2)

Q3) Explain square wave oscillator using a stable multivibrator?A3) The astable multivibrator shown in the figure below [Ref.1] can be used to generate square wave oscillations. The diode is connected across RB and the diode and capacitor are charged through RA to a voltage of 2/3 of VCC. The capacitor discharges through RB and Q1. The discharging of capacitor when reaches 1/3VCC the discharging stops.

Fig 1 Astable multivibrator as square wave oscillator Q4) Explain ramp generator using IC565?A4) The circuit diagram is shown below [Ref.1]. The transistor Q1 is turned on by the comparator 1 when voltage across capacitor is 2/3Vcc. The capacitor C discharges through Q1. When capacitor discharges the voltage across C is 1/3Vcc, comparator 2 turns off Q1. The time period is given asT = VCCC/3IC

Fig 2 Free Running Ramp generator circuit

Fig 3 Output waveformIC = (VCC-VBE)/RThe free running frequency of ramp generator is given byf0 = 3IC/VCCCThe output waveform is shown in above figure. Q5) Explain monostable multivibrator?A5)

This configuration consists of one stable and one unstable state. The stable state can be chosen either high or low by the user. If the stable output is set at high (1), the output of the timer is high (1). At the application of an interrupt, the timer output turns low (0). Since the low state is unstable it goes to high (1) automatically after the interrupt passes. The monostable multivibrator using IC555 is shown below.

Fig 4 Monostable multivibrator using 555The output is taken through pin 3. The supply is connected to pin 8. A small capacitor is connected to filter noise. The working is shown below in figure and explained as well.

Fig 5 555 connected as monostable multivibratorThe discharge transistor will go to saturation when the F/F is reset. The discharge of C takes place through drain of CMOS. During negative pulse comparator 2 compares the pulse with reference voltage of 1/3 Vcc and output is low until the input becomes greater than the reference voltage. The output of F/F is set high when the output goes below 1/3Vcc. The output at pin 3 is high.

Fig 6 Input and Output waveformWhen the C discharges the transistor is off and the voltage decays exponentially. This is input to the comparator 1 with reference voltage 2/3Vcc. The output is still high obtained at pin 3. The output of comparator is high when the threshold voltage becomes more than the reference voltage. Due to this the F/F is reset and output goes to zero. When the output is low the capacitor discharges completely and the transistor goes into saturation.Pulse width

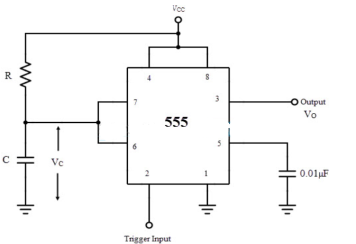
The voltage across C is Vc = Vcc (1-e-t/RC)

When voltage across capacitor is 2/3Vcc

2/3Vcc = Vcc (1-e-t/RC)

e-t/RC= 1/3

Taking log of both sides and solving we get

t= 1.098RC

The pulse width of rectangular pulse is 1.1RC (approx.)

Q6) Design a non-inverting active low pass filter circuit that has a gain of ten at low frequencies, a high-frequency cut-off or corner frequency of 175Hz and an input impedance of 20KΩ.A6)

The voltage gain of the non-inverting amplifier is given as

$A_{f}=1+\frac{R_{2}}{R_{1}} =10$

Now assume the value of R1 to be 1KΩ and calculate the value R2 from the above equation.

$R_{2}=(10-1)x R_{1}= 9x\times1k\Omega = 9k\Omega$

Hence for a voltage gain of 10, values of R1 and R2 are 1KΩ and 9KΩ respectively. Gain in dB is given as 20LogA = 20Log10 = 20dB

Now we are given with the cut-off frequency value as 175Hz and input impedance value as 20KΩ. By substituting these values in the equation and value of C can be calculated as follows.

$f_{c}= \frac{1}{2\pi RC}$

$C= \frac{1}{2\pi Rf_{c}}=\frac{1}{2\pi\times 175\times 20k\Omega}$ = 45.47nF

Q7) Assume Rs1 = Rs2 = 15KΩ and capacitor C1 = C2 = 100nF. The gain resistors are R1=1KΩ, R2= 9KΩ, R3 = 6KΩ, and R4 =3KΩ. Design a second-order active low pass filter with these specifications.A7) The cut-off frequency is given as

$\begin{align*} f_{c}=\frac{1}{2\pi RC} \end{align*}$

(1)

$\begin{align*} f_{c}=\frac{1}{2\pi \times 15\times 10^{3}\times 100\times 10^{-9}} \end{align*}$

$\begin{align*} f_{c}=106.10Hz\end{align*}$

The gain of first stage amplifier is

$\begin{align*} A_{1} = 1 +(R_{2}/R_{1}) \end{align*}$

$\begin{align*} A_{1} = 1 + \frac{9\times 10^{3}}{1\times 10^{3}} \end{align*}$

$\begin{align*} A_{1} =10 \end{align*}$

The gain of second stage amplifier is

$\begin{align*} A_{2} = 1 +(R_{4}/R_{3}) \end{align*}$

$\begin{align*} A_{2} = 1 + \frac{6\times 10^{3}}{3\times 10^{3}} \end{align*}$

$\begin{align*} A_{2} =3 \end{align*}$

Total Gain of the filter

$\begin{align*} A_{v} = 10\times 3 \end{align*}$

$\begin{align*} A_{v} =30 \end{align*}$

The total gain in dB

(2) $\begin{align*} A_{v} = 20 log(30) \end{align*}$

(3) $\begin{align*} A_{v} = 30dB \end{align*}$

The gain at cut-off frequency is

(4) $\begin{align*} \ Gain \ at f_{c} = 30dB -6dB = 24dB \end{align*}$

Q8) Consider cut-off frequency value as 10 KHz, pass band gain Amax as 1.5 and capacitor value as 0.02 µF.A8)

The equation of the cut-off frequency is fC = 1 / (2πRC)

By re-arranging this equation,

we have R = 1 / (2πfC)

R = 1/ (2π * 10000 * 0.02 * 10-6) = 795.77 Ω

The pass band gain of the filter is Amax = 1 + (R3/R2) = 1.5

R3 = 0.5 R2

If we consider the R2 value as 10KΩ, then R3 = 5 kΩ

We can calculate the gain of the filter as follows:

Voltage Gain for High Pass filter:

| Vout / Vin | = Amax * (f/fc) /√ [1 + (f/fc) ²]

Av(dB) = 20 log10 (Vout/Vin)

Q9) Design a filter with cut-off frequency 4 KHz and the delay rate in the stop band is 40dB/decade. As the delay rate in the stop band is 40dB/decade we can clearly say that the filter is second order filter.A9)

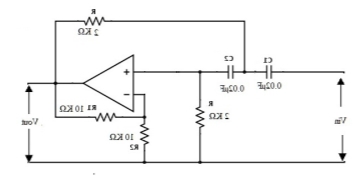
Let us consider the capacitor values as C1= C2 = C = 0.02µF

The equation of the cut-off frequency is fc = 1/ 2πRC Hz

By re-arranging this equation we have R = 1/ 2πfC

By substituting the values of cut-off frequency as 4 KHz and capacitor as 0.02µF

R = 1.989 KΩ = 2KΩ.

Let the gain of the filter is 1+ R1/R2 = 2

R1 / R2 = 1

R1 = R2

Therefore, we can take R1 = R2 = 10 KΩ

Thus, the obtained filter is shown as below:

Q10) Explain Inverting Schmitt Trigger circuit?A10)When comparator circuit used for zero crossing detector false triggering may takes place. The comparator circuit used to avoid such unwanted triggering is called regenerative comparator or Schmitt trigger. This basically uses positive feedback. The circuit diagram of basic Schmitt trigger is shown in figure. As the input is applied to inverting terminal it is an inverting Schmitt trigger. The inverting mode produces opposite polarity output. The output is fed back to the non-inverting input which is of same polarity as that of output, hence positive feedback. CASE I: When Vin is slightly positive than Vref. The output gets driven in to negative saturation i.e. –Vsat level. CASE II: When Vin is more negative than -Vref. The output gets driven in to positive saturation i.e +Vsat level. Thus, output voltage changes its state between +Vsat and –Vsat. Output voltage levels +Vsat and –Vsat are controlled by potential divider formed by R1.

Fig 7 Inverting Schmitt Trigger Circuit

Fig 8 Input and Output Waveform of Inverting Schmitt Trigger Circuit

Sign Up