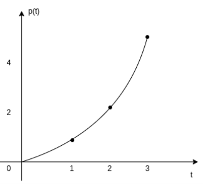
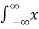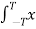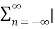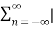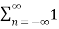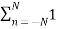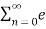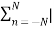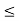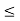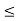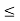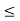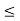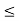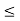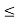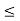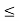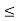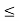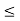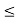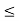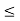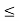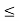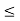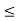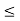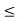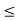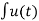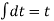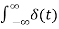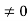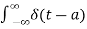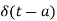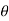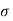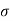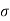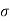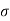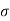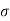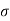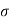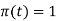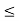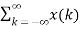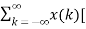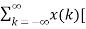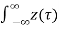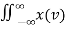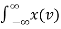A1) A signal is a description of how one parameter varies with another parameter. For instance, voltage changing over time in an electronic circuit, or brightness varying with distance in an image.

   Figure 1. Voltage change

   Figure 2. Picture Brightness

Picture brightness: A camera senses the incoming light and records the light reflectivity as a function of space onto a magnetic film.

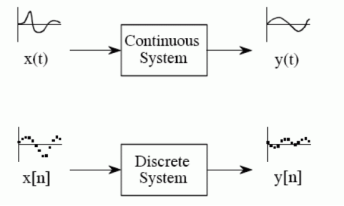
A2) A system is any process that produces an output signal in response to an input signal. This is illustrated by the block diagram in Figure.

Figure 3. System

Continuous systems input and output continuous signals, such as in analog electronics. Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.

Q3) Explain the classification of signals?

A3)

Deterministic

A signal is said to be deterministic if there is no uncertainty with respect to its value at any instant of time or the signals which can be defined exactly by a mathematical formula are known as deterministic signals.

Figure . Deterministic signal

Random

A signal is said to be non-deterministic if there is uncertainty with respect to its value at some instant of time. Non-deterministic signals are random in nature hence they are called random signals. Random signals cannot be described by a mathematical equation. They are modelled in probabilistic terms.

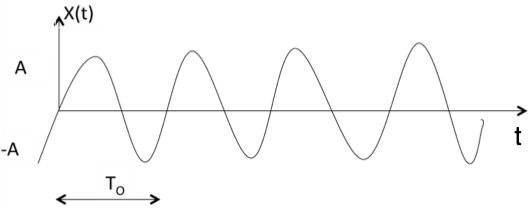
Figure . Random signal

Periodic

A signal is said to be periodic if it satisfies the condition x(t) = x(t + T) or x(n) = x(n + N).

Where

T = fundamental time period,

1/T = f = fundamental frequency.

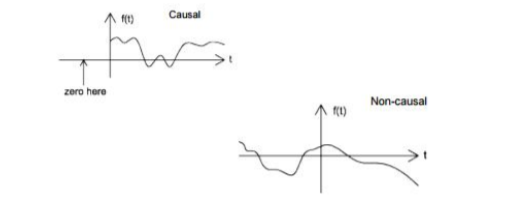
Figure . Random signal

The above signal will repeat for every time interval T0 hence it is periodic with period T0.

Non-periodic

Non-periodic signals (also known as aperiodic signals), unlike periodic signals, do not have just one particular frequency. Instead, they are spread out over a continuous range of frequencies. For example, a speech signal

Energy

A signal is said to be energy signal when it has finite energy

Energy E = 2(t) dt

Power:

A signal is said to be power signal when it has finite power.

Power P = lim T-> ∞ 1/2T   2 (t) dt

Causal and Non-casual

A system is said to be causal if its output depends upon present and past inputs, and does not depend upon future input. For non- causal system, the output depends upon future inputs also.

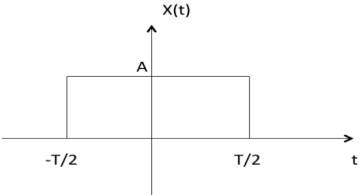
Figure . Casual and Non casual system

Even and odd signal.

A signal is said to be even when it satisfies the condition x(t) = x(-t)

Example 1: t2, t4… cost etc.

Let x(t) = t2

x(-t) = (-t)2 = t2 = x(t)

∴,∴, t2 is even function

Example 2: As shown in the following diagram, rectangle function x(t) = x(-t) so it is also even function.

Figure . Even signal

A signal is said to be odd when it satisfies the condition x(t) = -x(-t)

Example: t, t3 ... And sin t

Let x(t) = sin t

x(-t) = sin(-t) = -sin t = -x(t)

∴,∴, sin t is odd function.

Any function ƒ(t) can be expressed as the sum of its even function ƒe(t) and odd function ƒo(t).

ƒ(t ) = ƒe(t ) + ƒ0(t )

where

ƒe(t ) = ½[ƒ(t ) +ƒ(-t )]

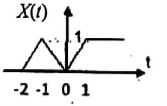
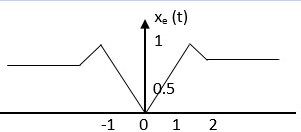
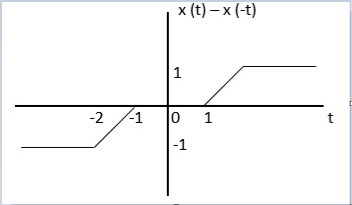
Q4) Find the even and odd of the signal as shown in the figure

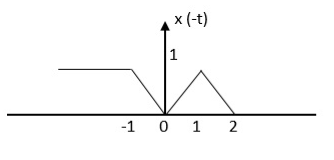
Step 1: Find the signal x(-t)

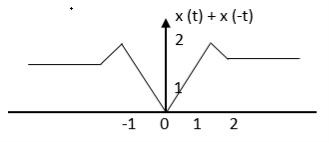
The even signal is xe(t) = x(t) +x(-t)

Therefore

xe(t) = ½ x(t) +x(-t)/2

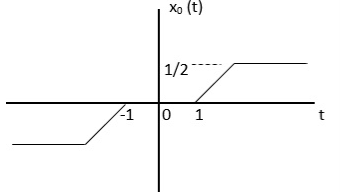
For odd the signal is

xo(t)

Q5) Find whether the following signals are periodic or not. Find its fundamental frequency.

A5)

a)     x1(t) = sin3t + sin πt

b)    x2(t) = 1.2 + sin3t

c)     x3(t) = 1.2 + sin πt

d)    x4(t) = -1.2 -2 sin 2.1t + 3 cos 2.8 t

a)     T1 = 2π/w1 = 2π/3       T2 = 2π/w2 = 2π/π=2

T1/T2 = 2π/3 / 2  = π/3 Irrational number hence aperiodic

b)    Clamped sinusoidal wo= 3rad/sec

c)     Clamped sinusoidal wo=π rad/sec

d)    T1 = 2π/w1 = 2π/2.1 = 20π/21

T2 = 2π/w2 = 2π/2.8 = 20π/28 = 5π/7

T1/T2 = 20π/21/5π/7 = 4/ 3

LCM = 3. Hence it is periodic

To = LCM x T1 = 3 x 20π/21 = 20π/7       wo = 2π/20π/7 = 7/10 = 0.7 rad/sec

Q6) Determine the values of power and energy of the signals :

A6) x(n) = sin(π/4n)

Energy is given by x(n) E= |x(n)| 2

E =   sin 2 (π/4n) |

= =   1-cos(π/2n)/2 |=∞

P = lim N->∞ 1/ 2N+1   - cos π/2 n/2 = ½ lim N->∞ 1/2N+1 = 2N+1

The energy is infinite, and the power is finite. Therefore, the signal is a power signal.

x(n) = e 2n u(n)

E = E= |x(n)| 2 = 1   4n  = 1+ e 4 + e 8 + ……………….+ ∞ = ∞

P = lim N->∞ 1/2N+1 x(n) | 2

=  lim N->∞ 1/2N+1 [ e 4(N+1) -1 / e 4 -1 ]   = ∞

The signal is neither power or energy signal.

Q7) Explain the basic operation on signals ?

A7) Time Shifting

Let us consider a signal x(t) as shown in figure. The time shifting of x(t) may delay or advance the signal in time. Mathematically this can be represented by

y(t) = x(t-T) ------------------------------------------(1)

If T is positive the shifting delays the signal as shown in figure.

If T is negative the shifting advances the signal as shown in figure.

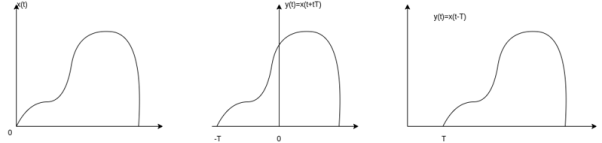
 Figure. Time Shifting

Similarly, the time shifting operation of discrete time signals is represented by

y(n) = x(n-k)

which shows that the signal y(n) can be obtained by shifting x(n) by k units. If k is positive the shift is to the right (delay) and if k is negative the shift is to the left . Let us consider a signal x(n) as shown in figure. The signal x(n-2) is obtained by shifting x(n-2) is obtained by shifting x(n) right by 2 units of time. The result is shown in fig (b). On the other hand x(n+3) is obtained by shifting x(n) left by three units of time.

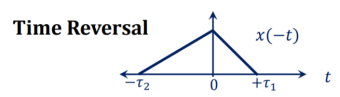
Figure . Time shifting using discrete signal

Time Reversal

The time-reversal of signal x(t) can be obtained by folding the signal about t=0. It is denoted by x(-t). The signal x1(t) and its reflection x(-t) are illustrated in fig a and b respectively.

Figure 24. Time Reversal for continuous time

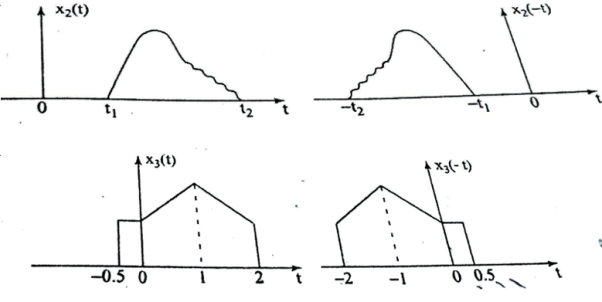
The signal x(-t+2) is obtained by delaying x1(-t) by two units of time and x1(-t-2) is obtained by advancing x1(-t) by two units of time. The signals x1(-t+2) and x1(-t-2) are shown in figure ( c) and (d).

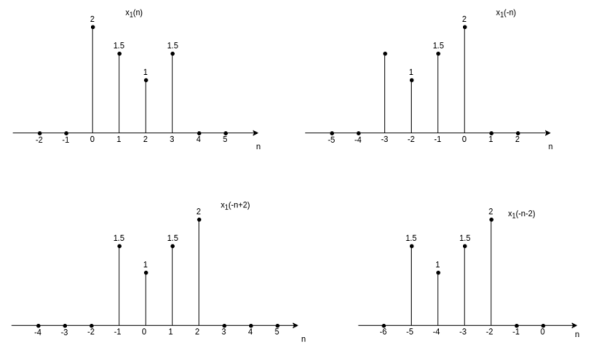
Figure . Time reversal for x2(t) and x3(t)

The time-reversal of the discrete-time signal can be obtained by folding the sequence x(n) about n=0. For signal x1(n) in fig, the time-reversal signal x1(-n) is shown in fig (b).

Figure . Time reversal for discrete time signal

The signal x1(-n+2) is obtained by delaying x1(-n) by two units of time and x1(-n-2) is obtained by advancing x1(-n) by two units of time. The other examples for time-reversal of discrete-time signal are obtained by fig (a) and (b).

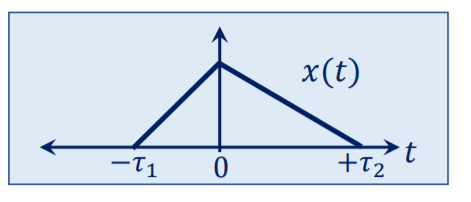
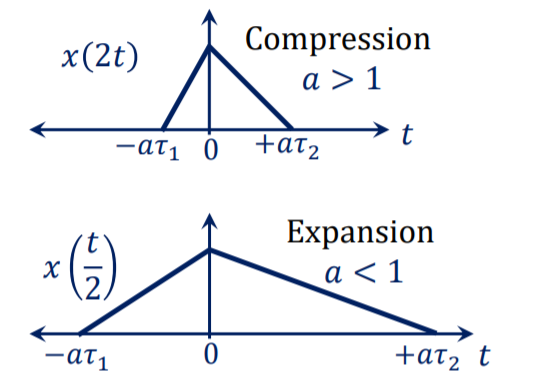
Time scaling:

Let us consider a signal x(t) as shown in figure(a). The time scaling of the signal can be accomplished by replacing t by at in signal x(t).

If a=2 we get new signal

y(t) = x(2t)

Observe that x(t) is switching from 0 to 1 at t=-1 and switching from 1 to 0 at t=3. . When y(t) = 2t, y(t) = x(2t), y(t) switches from 0 to 1 at t=0.5 and switches from 1 to 0 at t=1.5.

In the original signal x(t) magnitude is equal to 1 at t=0 and t=2 . But in a time-scaled signal y(t) magnitude is equal to 1 at t=0 and t=2. But in a time-scaled signal y(t) magnitude is equal to 1 at t=0 and t=1. This behavior shows that x(t) is compressed in time by factor 2.

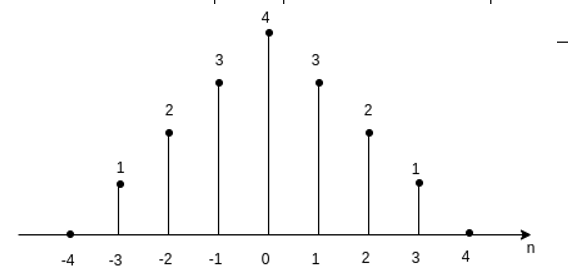
Figure . Time Scaling

The resulting signal x(2t) is shown in fig(b). Let x(t) be an audio signal. If x(t) were recorded on a magnetic tape then x(2t) is the signal played back twice the recording speed.

Now consider another signal y(t) = x(at) with a=1/2. Figure ( c ) shows x(1/2) which is expanded in time by factor 2.

In discrete- time signal

y(n) = x(2n)

Let x(n) be a sequence as shown in figure. Then we plot time scaled signal y(n) by substituting different values of n.

For n =-1

y(-1) = x(-2) =2

…..

y(0) = x(0) =4

y(1) = x(2) =2

y(2) = x(4) = 0

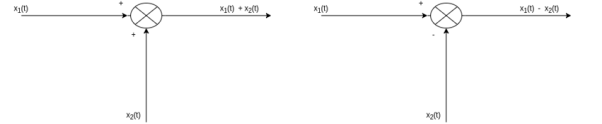
Figure . Discrete time signal

Signal addition:

The sum of two continuous-time signals can be obtained by adding their values at every instant. Similarly, the subtractions of two continuous-time signals can be obtained by subtracting their values at every instant.

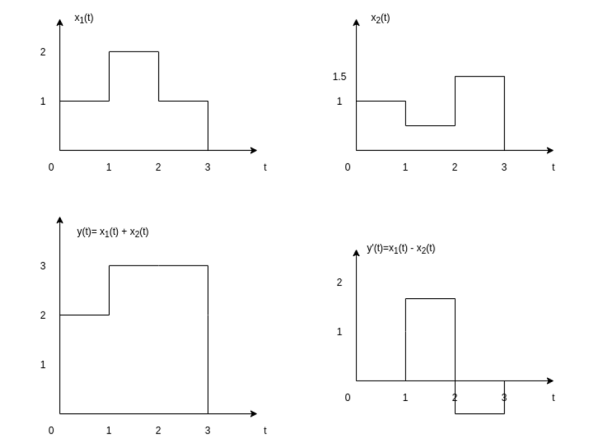
Figure . Signal addition

Let us consider the addition and subtraction of two signals x1(t) and x2(t) as shown in Figures (a) and (b).

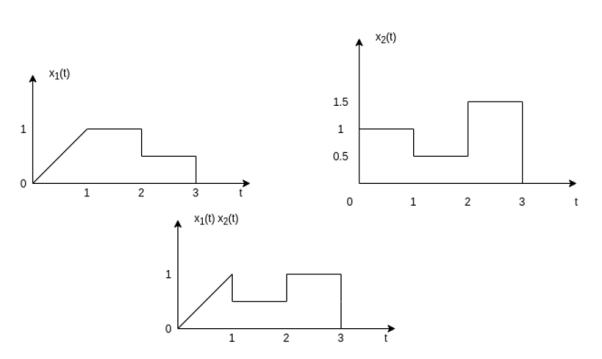
Figure . Resultant for addition of signals

The addition of signals of two signals x1(t) and x2(t) can be obtained by considering each time interval separately as follows:

x1(t) = 1    for 0 t 1  and

x2(t) =1     for 0 t 1 

Hence x1(t) + x2(t) = 2  for 0 t 1 

x1(t) = 2    for 1 t 2  and

x2(t) =0.5     for 1 t 2

 Hence x1(t) + x2(t) = 2.5  for 1 t 2

 x1(t) = 1    for 2 t 3  and

x2(t) =1.5     for 2 t 3

Hence x1(t) + x2(t) = 2.5  for 2 t 3

The sketch for y(t) = x1(t) + x2(t) as shown in fig ( c )

In the same way the subtraction of x2(t) from x1(t) can be obtained. By inspection we can find

y’(t) = x1(t) – x2(t)  = 0   for 0 t 1

                   = 1.5  for 1

                    = -0.5 for 2 t 3

For discrete-time signals, the sum of two sequences can be obtained by adding the sequence values at the same index n for which the sequences are defined.

Figure . Addition in discrete time signals

If x1(n) = {1, 3, 2, 1}   and

  x2(n) = {1, -2, 3, 2}

then

x1(n) + x2(n) = { 1+1, 3-2, 2+3, 1+2}= {2, 1, 5, 3}

x1(n) – x2(n) = { 1-1, 3-(-2), 2-3, 1-2} = { 0, 5, -1, -1}

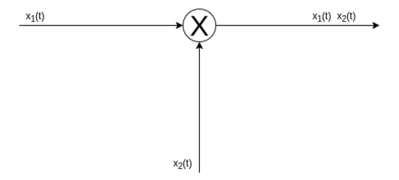
Signal multiplication   

The multiplication of two signals can be obtained by multiplying their values at every instant.

The multiplication process is illustrated in the figure.

In the interval 0 t 1

x1(t) = t; x2(t) = 1. Therefore y(t) = x1(t) x2(t)

Therefore y(t) = x1(t) x2(t)=t

In in the interval  1 t 2

x1(t) =1; x2(t) = 0.5. Therefore y(t) = 0.5

In in the interval  2 t 3

x1(t) =0.5; x2(t) = 1.5. Therefore y(t) = 0.75

Figure . Signal Multiplication

If x1(n) = { 1, 2, -2, 3} and x2(n) = {1, 0.5, 0.5, 1} then

y(n) = x1(n) . x2(n) ={ 1.1, 2.(0.5), -2(0.5), 3.1}

={1, 1, -1, 3}

Q8) Write a short note on elementary signals?

A8)

1. Unit step function

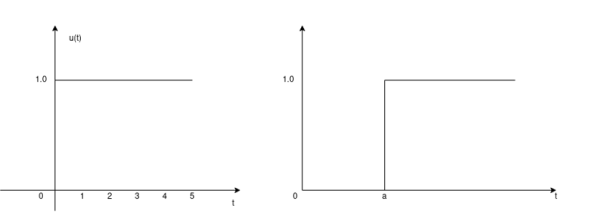
The unit step sequence is defined as:

u(t) = 1 for t

     = 0 for t<0

From the above equation we find the when the argument t in u(t) is less than zero then the unit step function is zero and when the argument t in u(t) is greater than or equal to zero then the unit step function is unity

Similarly, for a shifted unit step function u(t-a) is zero if the argument (t-a) <0 or t<a and is one if the argument (t-a) > 0 or t>a.

That is

u(t-a) = 1  for  t>a

       =0    for t<a

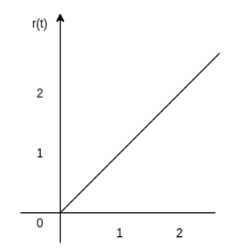
Figure3. Step function

Unit ramp function

The unit ramp function is defined as:

r(t) = t    for t

    =0    for t<0

or

r(t) = t u(t)

Figure 4. Ramp function

The ramp function can be obtained by applying unit step function to an integrator.

r(t) = dt =     ( in the time interval t>0)

The unit step function can be obtained by differentiating the unit ramp function

Thus

u(t) = d/dt r(t)

Unit parabolic function

The unit parabolic function is given by

p(t) = t 2 / 2      for t 0

    = 0          for t<0

Figure5. Unit parabolic function

Or

p(t) = t2/2 u(t)

Impulse function

The impulse function occupies an important place in signal analysis. It is defined as

dt =1

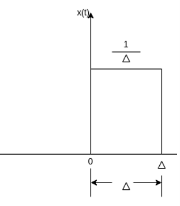
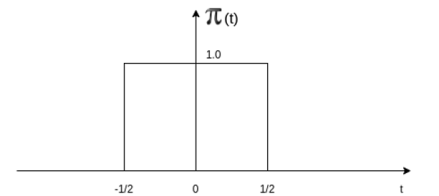
and

δ(t) =0  for t

The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using limiting process on the rectangular pulse as shown in figure.

Note that the area under the rectangular pulse is equal to unity.

Figure6. Impulse function

The rectangular pulse function of the figure can be expressed as

x(t) = 1/ ∆ [ u(t) – u(t-∆)] …………………………………..(1)

The impulse function can be obtained when the width ∆ ->0 that is

 δ(t) = lim ∆-> 0 x(t)

= lim ∆-> 0 1/ ∆ [ u(t) – u(t-∆)]

Figure7. Delayed impulse function

The delayed unit impulse function is defined as

=1     for t=a

and =0    for t a

Figure8. Unit impulse function

Sinusoidal signal 

A continuous time sinusoidal signal is given by

x(t) = A sin ( + ) ---------------------------------(1)

where A is the amplitude, Ω is the frequency in radians per second, and is the phase angle in radians.

Figure shows the waveform of sinusoidal signal with A=1, = -π/3 with period 2π/Ω.

Figure 9. Sinusoidal signal

Real exponential and complex exponential

Real exponential

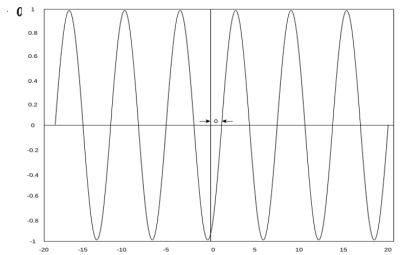
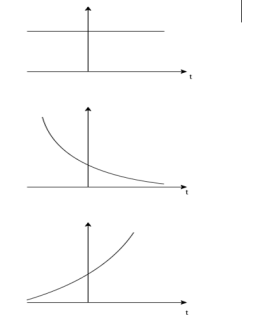
Figure10. Real exponential signals

A real exponential signal is defined as

x(t) = A e at --------------------------------(1)

where both A and a are real. Depending on the value of ‘a’ we get different signals. It ‘a’ is positive the signal x(t) is growing exponential as shown in fig(b) If ‘a’ is negative then x(t) is decaying exponential as shown in fig(c). For a=0 x(t) is constant.

Complex exponential signal.

The most general for of complex exponential signal is given by

x(t) = e st ---------------------------------------(1)

where s is a complex variable defined as

s = + j Ω

Therefore

x(t) = e st = e s(+ j Ω) = e t . e j Ωt

Using Euler identity, we can expand

e j Ωt = cos Ω t + j sin Ωt

substituting in eq(1) we get

x(t) = e t [ cos Ω t + j sin Ω t]

Depending on the values of and Ω we get different signals.

1. If =0 and Ω =0 x(t) = 1 that is the signal x(t) is a pure DC signal.
2. If Ω=0 then s = , x(t) = e t which decays exponentially for <0 and grows exponentially for > 0.
3. If =0 then s= jΩ gives x(t) = e j Ωt a sinusoidal signal with ɸ=0
4. If <0 with finite Ω we get exponentially decaying sinusoidal signal.
5. If 0 with finite Ω we get exponentially growing sinusoidal signal.

Figure 11. Complex exponential signal

Rectangular Pulse:

The rectangular pulse function is defined as

Figure 12. Rectangular pulse

     for |t| ½

     =0     otherwise

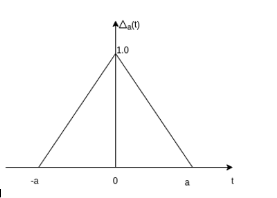
Triangular pulse function

The unit triangular function is defined as

∆a(t)   =      1 - |t|/a       |t| a

               0             |t| a

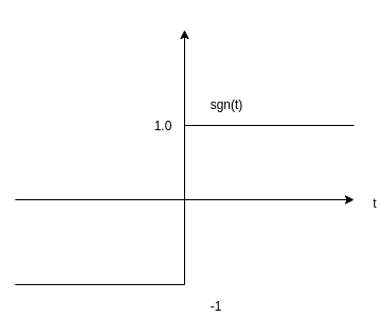
Figure13. Triangular pulse function

Signum function

The sinc function is defined by the expression

sinc(t) = sin t/t          -∞ < t < ∞

Figure 14.sinc function

The sinc function oscillates with period 2π and decays with increasing t. Its value is zero at nπ, n = ±1, ±2, …………………….. It is an even function of t.

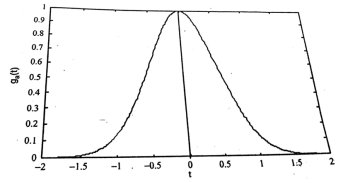
Gaussian function:

Figure 15. Gaussian function

The Gaussian function is defined by the expression

ga(t) = e – at ^2  - ∞ <t<∞

This function is extensively used in probability theory.

Problems:

Sketch the continuous time signal x(t) = 2 sin πt for interval 0 2. Sample the continuous time signal with sampling period T =0.2 sec and sketch the discrete time signal.

Solution:

Given:

                  x(t) = 2 sin πt

To sketch the signal we have values x(t) for different values of t, that is

x(0) = 2 sin π (0) = 0.

x(0.25) = 2 sin π (0.25) = √2

x(0.5) = 2 sin π (0.5) = 2

x(0.75) = 2 sin π (0.75) = √2.

x(1) = 2 sin π (1) = 0

x(1.25) = 2 sin π (1.25 = -√2

x(1.5) = 2 sin π (1.5) = -2.

x(0.25) = 2 sin π (1.75) = - √2

x(2) = 2 sin 2π =0

Take t on x-axis and x(t) on y-axis. Mark the above points and join all the points by a smooth curve to get continuous signal as shown in fig (a) . Given sampling period T =0.2

Q9) Explain parallel connection of systems?

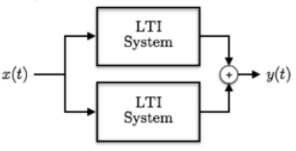
A9) Consider two LTI systems with impulse responses h1(n) and h2(n) connected in parallel as shown in fig(a)

Figure . Parallel connection

From the figure the output of the system1 is

y1(n) = x(n) * h1(n)

and the output of system 2 is

y2(n) = x(n) * h2(n)

= h1(n-k) + h2(n-k)

= h1(n-k) + h2(n-k) ]

= h1(n-k) + h2(n-k) ]

= x(n) * h(n) where h(n) = h1(n) + h2(n)

Thus, if the two systems are connected in parallel then the overall impulse responses is equal to the sum of the two impulse responses.

Q10) Explain cascade connection of systems?

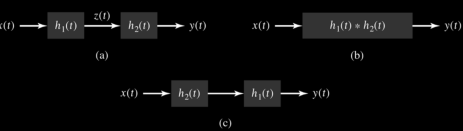
A10) Consider the cascade connection of two LTI systems, as illustrated in Fig. (a). Let z(t) be the output of the first system and therefore the input to the second system in the cascade.

The output is expressed in terms of z(t) as 𝑦 (𝑡) = 𝑧(𝑡) ∗ ℎ2(𝑡)

Substituting for z(t), we get

y(t) = h2(t-τ) dτ

Putting for z(t) we get

y(t) =  h1(τ-v) h2(t-τ) dv dτ

= h(t-τ) dv

= h(t) * h(t)

Figure . Cascade connection

Interconnection of two LTI systems. (a) Cascade connection of two systems. (b) Equivalent system. (c) Equivalent system: Interchange system order.