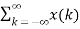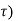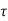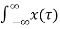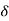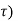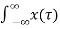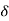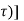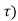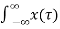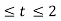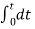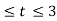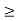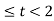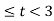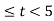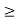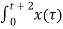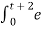A3) If the input to the system is unit impulse response, then the output of the system is known as impulse response of the system denoted by h(n). That is

h(n) = T [ δ(n)]…………………………………………………………..(1)

The arbitrary sequence x(n) can be represented as weighted sum of discrete impulses given by

x(n) =    δ(n-k) --------------------------------------------(2)

Then the output

y(n) = T [     δ(n-k)] -----------------------------------------------------(3)

A4)

h[n] = δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]

x[n] = δ[n-2] - δ[n-4]

x[n] * h[n] = x[n] * { δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]}

= x[n] + x[n-1] + x[n-2]+ x[n-3]+ x[n-4]+ x[n-5]

y[n] =  δ[n-2]- δ[n-4]+ δ[n-3]- δ[n-5] + δ[n-4]- δ[n-6]+ δ[n-5]- δ[n-7] - δ[n-6]+ δ[n-8]- δ[n-7]+ δ[n-9]}

= δ[n-2]+ δ[n-3]-2 δ[n-6]-2 δ[n-7] + δ[n-8]+ δ[n-9]

y[n] = {0,0,1,1,0,0,-2,-2,1,1}

A5) Using linear property of the system the interchange operator T with the summation k to obtain

y(n) =  [    T δ(n-k)] ----------------------------------------------(4)

The response to the shifted impulses is represented as h(n,k)

h(n,k) = T[ δ(n-k)]

Now

y(n) =    h(n,k)   -----------------------------------------------------------(5)

For time-invariant system

h(n,k) =h(n-k) ----------------------------------------------------------------------(6)

Substituting (6) in (5) we get

y(n) =    h(n-k)   ------------------------------------------------------------------(7)

Thus, the output of the LTI system is given by the weighted sum of time-shifted responses.

The sum in eq(7) is termed as convolution sum which is given by

y(n) = x(n) * h(n)   -----------------------------------------------------------------------------(8)

* denotes convolution operation.

A6) We know that for discrete time system, convolution of two sequence can be given by:

y(n) = x(n) * h(n) = ∑ x[i]h[n-i]

Where * denotes the convolution operator, and

where i ranges from -∞ to +∞

Hence y(n) = [3, 6+2,3+4+1,6+2+2+2,4+1+4,2+2,4]

=>y(n) = [3,8,8,12,9,4,4]

A7) Consider an LTI system which is initially related at t=0. If the input of the system is an impulse, then the output of the system is denoted by h(t) is called the impulse response of the system.

 We can denote

h(t) = T [ δ(t)]

 We know that any arbitrary signal x(t) can be represented as

x(t) = ( t-d           ------------------------------------------------------(1)

 The system output is given by

y(t) = T[x(t)]   --------------------------------------------------------------------------------(2)

Substituting (1) in (2)

y(t) = T [   ( t-d      --------------------------------------------------------(3)

For linear system

  y(t) =  [ T[ ( t-d  --------------------------------------------(4)

If the response of the system due to impulse δ(t) is h(t) then the response of the system due to delayed impulse is

h(t,  = T [ δ(t-T)] --------------------------------------------------------------(5)

Substituting (5) in (4) we get

 y(t) =  [ h(t,τ) dτ  -------------------------------------------------------(6)

For a time invariant system the output due to the delayed input by T is equal to delayed output by T, That is

 h(t,τ) = h(t-τ) ---------------------------------------------------------------(7)

Substituting (7) in (6) we get

y(t) =   h(t-τ) dτ   -----------------------------------------------------------(8)

This is called convolution Integral. The convolution of two signal x(t) and h(t) can be represented as

y(t) = x(t) * h(t)

A8) The procedure is as follows:

1. For the given signals x(t) and h(t) graph the signals x(τ) and h(τ) as a function of independent variable τ.
2. Obtain the signal h(t-τ) by folding h(τ) about τ=0 and then time shifting by time t.
3. Graph both signals x(τ) and h(t-τ) on the same τ-axis beginning with very large negative time shift t.
4. Multiply the two signals x(τ) h(t-τ) and integrate over the overlapping interval of  two signals to obtain y(t)
5. Increase the time shift and take the new interval whenever the function of either x(τ) and h(t-τ) changes. The value of t at which the change occurs defines the end of the current interval and beginning of a new interval. Calculate y(t) using step 4.
6. Repeat steps 5 and 4 for all intervals.

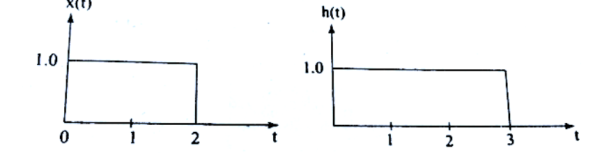
A9) x(t) =1                                    0

       = 0                                   otherwise

Fig . x(t) and h(t)

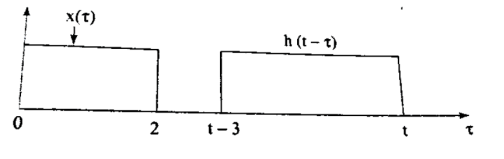
Figure : x(τ) and h(t-τ)

As shown in Figure the signals x(τ) and h(t-τ) does not overlap for t<0. Therefore the product x(τ) h(t-τ) is zero.

That is,

y(t) = h(t-τ) =0            for t<0

Now the shift the signal h(t-τ) right until the right edge of the signal h(t-τ) intersects left edge of x(τ).

In the interval 0

y(t) = = t

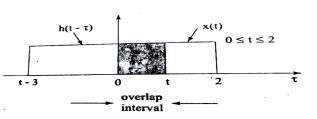
Figure . Product of x(t) and h(t-τ)

In the interval 2 

y(t) = = 2

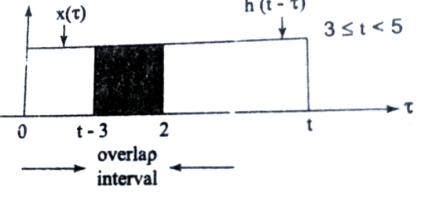
In the interval 3

Figure . Product of h(t-τ) x(τ)

y(t) =  = 2 – (t-3)

= 5-t.

For t

Figure. Product of x(τ) h(t-τ) for t 5

The signals x(τ) and h(t-τ) do not overlap. Therefore y(t)=0.

y(t) = 0   for t<0

       =  t     for 1

       = 2     for  2

       = 5-t   for 3

       =0       for t 5.

The sketch y(t) is as shown in figure

Figure . The output waveform

A10) Given:

x(t) = e -2 u(t)                                            h(t) = u(t+2)

Figure . x(t) and h(t)

Figure . Product exponential signal and unit step signal

Figure10. Product of exponential signal and delayed unit step signal

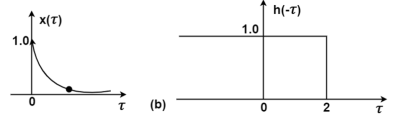
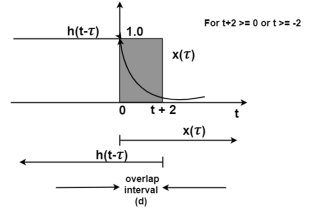
Figure . The output waveform

Figure (a) shows x(t) and h(t) . Fig (b) shows x(τ) and h(-τ) as functions of τ. The function h(-τ) can be obtained by folding the signal h(τ) about τ=0.

Figure (c ) shows that signal h(t-τ) is sketched for t<-2 by shifting h(τ) to left. For t<-2 x(τ) and h(t-τ) does not overlap and the product x(τ) h(t-τ) =0 that is

y(t) =0 for t<-2

Now increase the time shift until the signal h(t-τ) intersects x(τ). Figure (d) shows the situation for t>-2.

Here x(τ) =0   for τ <0  and h(t-τ) does not overlap and the product x(τ) h(t-τ) =0 that is

y(t)=0      for t<-2

Now increase the time shift t until the signal h(t-τ) intersects x(τ).

Figure (d) shows the situation for t>-2. Here x(τ) and h(t-τ) overlapped. But x(τ) =0 for τ<0 and h(t-τ) = 0 for τ > t+2. Therefore, the integration interval is from τ=0 to τ=t+2

y(t) =   h(t-τ) dτ

= =   -2τ  dτ

= -1/2  e -2 τ    | 0 t+2

= -1/2 [ e -2 (t+2) -1]

= 1 – e -2(t+2)   /2

y(t) = 0         for t<-2 

= 1 – e-2(t+2)/2                                 for t -2