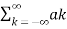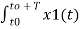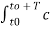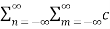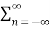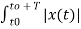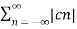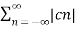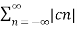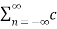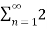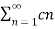A2)

Given a periodic sequence x[k]  with period N the Fourier series representation for x[k] uses N harmonically related exponential functions

 e j2πkn/N                    k=0,1,………….. N-1

The Fourier series is expressed as

x[k] =    e j2πnk/N

The Fourier co-effecients cn are given gy

cn = 1/N   e- j2πnk/N

A3) A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).

Where T = fundamental time period,

ω0= fundamental frequency = 2π/T

There are two basic periodic signals:

x(t)=cosω0t

x(t)=cos foωot (sinusoidal) &

x(t)=ejω0t

These two signals are periodic with period T=2π/ω0T=2π/ω0.

A set of harmonically related complex exponentials can be represented as {ϕk(t)}

ϕk(t)={ejkω0t}={ejk(2πT)t} where k=0±1,±2..n.....(1)

All these signals are periodic with period T

According to orthogonal signal space approximation of a function x (t) with n, mutually orthogonal functions is given by

x(t) = e jkwot  -----------------------------------------------(2)

= k e jkwot

Where ak= Fourier coefficient = coefficient of approximation.

This signal x(t) is also periodic with period T.

Equation 2 represents Fourier series representation of periodic signal x(t).

The term k = 0 is constant.

The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.

The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...

The term k=±n having fundamental frequency nω0, is called as nth harmonics.

A4) Linearity Property

If x(t) -- fxn

y(t) - fyn

then linearity property states that

a x(t) + by(t) - a fxn + b fyn

Time Shifting Property

If x(t) ------------ fxn

Then time shifting property states that

x(t-to)  -------- e -jnwot fxn

A5) Frequency Shifting Property

If x(t) -- fxn

Then frequency shifting property states that

e jnwoto . x(t) ----- fx(n-no)

Time Reversal Property

If x(t) -- fxn

Then time reversal property states that

If x(-t) --- f-xn

A6) If x(t) -- fxn

Then differentiation property states that

If dx(t)/dt -- jnwo.fxn

And integration property states that

If dt --- fxn/jnwo

A7)If x(t) -- fxn

Then multiplication  property states that

x(t) y(t) -- T fxn * fyn

and the convolution property states that

x(t) * y(t) -- T fxn.fyn

The convolution theorem or property states that , The Fourier series of the convolution of two time domain functions x1(t) and x2(t) is equal to the multiplication of their Fourier series coefficients, i.e.”Convolution of two functions in time domain is equivalent to multiplication of their Fourier coefficients in frequency domain”.

A8)Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then

1/T    x2(t)   =  1/T n  e j n Ωot [   m e jmΩot  ]    dt---------------------(1)

= 1/T     n d *m           e j(n-m)Ωot  dt ------------------------------(2)

= 0     n≠ m

= n d *n   n=m --------------------------------(3)

If x1(t) = x2(t) = x(t) then eq(3) becomes

1/T     2 =   2     --------------------------------(4)

The above equation can be written as

  2     = c0 2 +   2    

                                          n≠0      

                             = c0 2 +   n c *n     

                                          n≠0 

a0 2 + [Re(c 2 n ) + Im (cn ) 2]

 = a0 2 + 2 n /2 + b 2 n /2 ---------------------------(5)

A9) If x(t)  fxn

Then the conjugate property states that

x*(t)  f*xn x*(t)

Conjugate symmetry property for real valued time signal states that

f*xn = f-xn

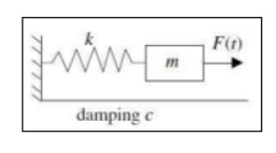
A10)Consider a mass spring system where we have mass m on spring with spring constant k with damping c and force F(t) applied to the mass. Suppose the forcing function F(t) is 2L periodic for some L>0 . The equation governs as

mx”(t) + cx’(t) +kx(t) = F(t)

Figure 4. Mass Spring system

The general solution consists of complementary solution xc which solves the associated homogeneous equation mx”+cx’+kx =0 and the particular solution of (1) we call xp.

For c>0 the complementary solution xc will decay as time goes by. Therefore we are interested in particular solution xp that does not decay and is periodic with the same period as F(t).

mx” +kx =0 has the general solution

x(t) = A cos(wt) + B sin(wt)

where

wo = √k/m

Any solution to mx”(t) +kx(t) = F(t) is of the form A cos(wt) + B sin(wt) +xsp

The steady periodic solution xsp has the same period as F(t)

Hence

F(t) = co/2 +    cos(nπ/L) + dn sin(nπ/Lt)

Hence,

x(t) = ao/2 +    cos(nπ/L) + dn sin(nπ/Lt)

Speech or music recognition

Any wave can be written as sum of sines and cosines. So for example if voice is recorded for one second the Fourier series is given by

voice= sin(x) + 1/10 sin(2x) + 1/100 sin(3x) +………

this module shows when you add sines /cosines the graph of cosines and sines becomes closer and closer to the original graph. Hence Fourier series is a wave that can be approximated and second the Fourier series converge fast. Hence it is used in compression. MP3 format uses audio compression.