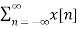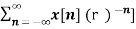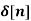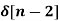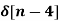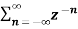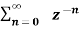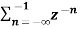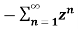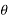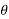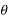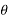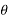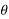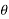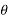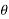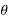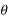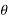undefined | unit 7 z transforms

Back to Study material

Unit 7Z transformsQ1) Explain Region of Convergence?The z-transform is important technique, used in areas of signal processing, system design and analysis and control theory.The formula used to convert a discrete time signal x[n] to X[z] is as follows:

X(z) = z-n

where x[n] is the discrete time signal and X[z] is the z-transform of the discrete time signal. Z-transform comes in two parts. The first part is the formula as shown above The second part is to define a region of convergence for the z-transform.Both parts are needed for a complete z-transform as a z-transform without a ROC would not be of much help in signal processing. Q2) Derive the expression for z transform?The Z transform for discrete time system x(n ) is defined as X(z) =

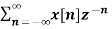------- (1) where z is a complex variable.

In polar form z can be expressed as

z = r e jw ---------------(2) where r is the radius of a circle

For n≥ 0

X(z ) = --------- (3)which is called one-sided z-transform.

By substituting z = r e jw

X(r e jw) = (r e jw) –n ------- (4)

e- jwn ----- (5)

Equation(5) represents the Fourier transform of the signal x(n) r-n

Hence the inverse DTFT X(r ejw) must be x(n) r-n.

x(n) r-n = 1/2π r e jw ) e jwn dw

On multiplying both sides by rn we get

x(n) = 1/ 2 π r ejw) (r ejw ) n dw [ z = r ejw

Let z= r e jw and dw= dz/jz

dz = r ejw dw

dw = dz/jre jw

x[n] = 1/ 2πj z n-1 dz

Q3) If X(z)= 4 – 5 z-2 + z-3 – 2z -4 then find x[n] Solution:

x[n] = 4 - 5 + - 2

Q4) Explain the properties of ROC?

The ROC is a ring or disk in z-plane centered at the origin.

The ROC cannot contain any poles.

If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.

If x(n) is a finite duration anti-casual sequence then the ROC is the entire z-plane except at z=∞.

If x(n) is a finite duration two- sided sequence the ROC is entire z-plane except at z=0 and z=∞.

If x(n) is infinite duration two- sided sequence ROC will consist of a ring in z-plane bounded on the interior and exterior by a pole not containing any poles.

The ROC of an LTI stable system contains the unit circle

ROC must be connected region.

Q5) Find the z-transform and ROC of the signal x(n) = an u(n) Solution:

X(z) =

= an u(n) -----(1) u(n) = 0 for n<0

1 for n≥0

= an ------- (2)

= n ------- (3)

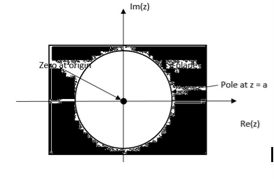
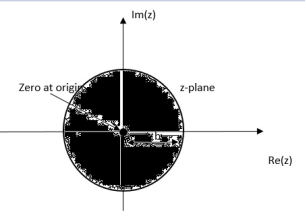
This is a geometric series of infinite length that is

a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1

Then from equation (3) it converges when |az-1| < 1 or |z| >|a|

Therefore

X(z) = 1/ 1-az-1: ROC |z| > |a|

Figure . ROC |z| > |a|Q6) Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC

X(z) =

X(z) = bn u(-n-1) u(-n-1) =0 for n ≥0

= 1 for n

≤ -1

= bn = b-1 =

= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1 |z| < |b|

Figure . ROC |z| < |b|Q7) Find the z transform of x(n) = cos n

u(n)

X(z) =

= ejn + e-jn/2] z -n

= ½ [ e j z -1 ) n += -j z -1 ) n ]

Both the series converges if [ e j z-1| <1 and | e j z -1 | <1 which implies |z|>1

Now X(z) = ½ [ 1/1 – e j z -1 + 1/ 1 – e -j z -1 ]

= ½ [ 1 – e -j z -1 + 1 – e j z -1 / 1 – e j z -1 – e -j z -1 + z -2

e j + e -j = 2 cos

= ½ [ 2 – 2 z -1 cos / 1 – 2 z-1 cos + z -2 ]

= 1-z-1 cos / 1 – 2 z-1 cos + z -2

Q8) Determine the signal x(n) whose z-transform is given by X(z) = log(1- az-1)

X(z)= log(1-az-1)

Differentiating both sides we get

d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1

-z d/dz { X(z)} =-az-1/1-az-1

= -az-1[ 1/1-az-1]

= -a Z[ a n-1 u(n-1)] -------- (1)

From differentiation property

Z{ n x(n)} = -z d/dz [ X(z)] ------- (2)

Comparing (1) and (2) we get

n x(n) = -a [ a n-1 u(n-1)]

or x(n) = -a [a n-1 u(n-1)]/n

Q9) Find the inverse z transform of X(z) = z+0.2/ (z+0.5) (z-1) |z|>1

X(z) = z+0.2 / z2 -0.5z -0.5

Divide the numerator by denominator

z-1 + 0.7 z-2 + 0.85 z-3 + 0.775 z-4

x2 -0.5z -0.5

z+0.2

z -0.5 -0.5 z -1

0.7 + 0.5 z-1

0.7 -0.35 z-1 -0.35 z-2

0.85 z -1 + 0.35 z-2

0.85 z-1 -0.42 z-2 -0.425 z-3

0.775 z -2 + 0.425 z-3

0.775 z-2 -0.387 z-3 – 0.3875 z-4

X(z) = z-1 + 0.7 z-2 + 0.85 z-3 + 0.775 z -4 + …………………………….

Q10) Find the partial fraction method of

X(z) = ¼ z-1

(1 – ½ z-1)(1-1/4 z-1)

X(z) = A + B

Z (1-1/2z-1) (1 – ¼ z-1)

By solving A= 1 and B=-1

Therefore,

X(z) = z - z

z-1/2 z-1/4

x(n) = (1/2) n u(n) – (1/4) n u(n)

Sign Up