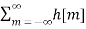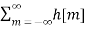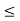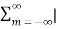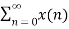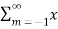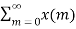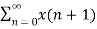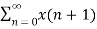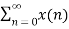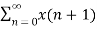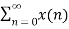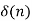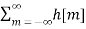undefined | unit 8 z transforms 2

Back to Study material

Unit 8Z transforms 2Q1) Explain casual LTI systems ?An LTI system is causal if its output y[n] depends only on the current and past input x[n] but not the future.Assuming the system is initially at rest with zero output y[n] | n<0 =0 then its response y[n] = h[n] to an impulse x[n] = δ[n] at n=0 is at rest for n<0 that is h[n] = h[n] u[n]Its response to a general input x[t] is:y[n] = h[n] * x[n] =

x[n-m] =

x[n-m]Due to the properties of the ROC, we know thatIf an LTI system is causal (with a right sided impulse response function h[n]=0 for n<0, then the ROC of its transfer function H(z) is the exterior of a circle including infinity.In particular, when H(z) is rational, then the system is causal if and only if its ROC is the exterior of a circle outside the out-most pole, and the order of numerator is no greater than the order of the denominator.Q2) Explain stable LTI systems?An LTI system is stable if its response to any bounded input is also bounded for all n:

if |x[n]| < Bx then |y[n]| < ∞

As the output and input of an LTI is related by convolution, we have:

y[n] = h[n] * x[n] = x[n-m] <∞

and

|y[n]| = | x[n-m]| Bx h[m]| <∞

which obviously requires:

h[m]| <∞

In other words, if the impulse response function h[m] of an LTI system is absolutely integrable, then the system is stable. We can show that this condition is also necessary that is all stable LTI systems' impulse response functions are absolutely integrable.Q3) Explain the transform analysis of LTI systems?Due to its convolution property, the z-transform is a powerful tool to analyze LTI systems

y[n] = h[n] * x[n] - Y(z) = H(z) X(z)

When the input is the eigenfunction of all LTI system, i.e x[n] = e sn = z n

The operation on this input by the system can be found by multiplying the system's eigenvalue H(z) to the input:

y[n] = O[z n] = h[n] * z n = H(z) z n

Q4) Explain unilateral z transform?

The Unilateral z-transform is also called as one-sided z- transform.

It is defined for n

0 that is causal sequences.

The unilateral z- transform is used to solve difference equations with initial conditions.

X(z) = z-n

Unilateral and bilateral transforms are same for causal signals.

Q5) Explain the properties of unilateral z transform?Properties of Unilateral Z transform

Time Shift

x(n) -> X(z)

x(n-1) => z -k X(z) + z -k+1 x(-1) + --------------+ z-1 x(-k+1) + x(-k)

x(n)  X(z)

x(n-1) -> Y(z)

Y(z) = (n-1) z -n

Let n-1=m

Y(z) = (m) z m+1

Y(z) = x(-1) + z -1 z -m

x(n-1) - z-1 X(z) + x(-1)

x(n-2) -> z -2 X(z) + z-1 x(-1) + x(-2)

Final Value Theorem

x(∞) = lim n->∞ (1-z-1) X(z)

Final value and initial value theorems are valid only for causal and stable system.

x(n +1) -> z X(z) – z x(0)

x(n) -> X(z)

z -n = z X(z) – z x(0)

x(n)  X(z)

X(z) = z -n

Subtracting these two equations

z -n - z -n = (z-1) X(z) – z x(0)

Taking the limit as $\displaystyle z \rightarrow 1$

- = lim z->∞(z-1) X(z)

Let us expand the LHS os the above equation as n->∞

x(∞) = lim n->∞ (1-z-1) X(z)

x(∞) = lim n->∞ (z-1) X(z)

Initial Value Theorem

x(n) -> X(z)

x(0) = lim z-> ∞ X(z)

X(z) = z -n

X(z) = x(0) + x(1)/z+x(2)/z2 +--------

Lim z->∞ X(z) = x(0)

Q6) Find the impulse response for the following systems:

y(n) = - ¾ y(n-1) + 1/8 y(n-2) = x(n)

y(n) - ¾ y(n-1) + 1/8 y(n-2) = x(n)

Taking z-transform on both sides we get

Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)

Substituting y(-1)=y(-2)= 0

Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

Y(z) = 1____________

1- ¾ z-1 + 1/8 z-2

Impulse response

x(n) = X(z) =1

Y(z) = 1____________ = 1____________

1- ¾ z-1 + 1/8 z-2 1- ¾ z-1 + 1/8 z-2

Y(z) = z__________ = A___ + B__

X(z) (z-1/2)(z-1/4) (z-1/2) (z-1/4)

By solving A=2 and B=-1.

Y(z) = 2 z - z

z-1/2 (z-1/4)

y(n) = 2 (1/2)n u(n) – (1/4) n u(n).

Q7) Find the step response for the following system

n) = u(n) X(z) = z/z-1

Y(z) = 1_______

X(z) 1-3/4 z-1 + 1/8 z-2

Y(z) = z z2___________

z-1 z2 -3/4 z +1/8

Y(z) = z2___________

z z2 -3/4 z +1/8

Y(z) = z2___________

z (z-1)(z-1/2)(z-3/4)

= A + B + C

z-1 z-1/2 z- 1/4

By solving A=8/3 B= -2 C= 1/3

Therefore

Y(z) = 8 . z -2 z + 1/3 z

3 z-1 z-1/2 z-1/4

y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)

Q8) Explain the advantages of z-transform?

Z transform is used for the digital signal.

Both Discrete-time signals and linear time-invariant (LTI) systems can be completely characterized using Z transform.

The stability of the linear time-invariant (LTI) system can be determined using the Z transform.

Q9) Explain the applications of z-transform?The field of signal processing is essentially a field of signal analysis in which they are reduced to their mathematical components and evaluated. One important concept in signal processing is that of the Z-Transform, which converts unwieldy sequences into forms that can be easily dealt with Z-Transforms are used in many signal processing systems.  Z-transforms can be used to solve differential equations with constant coefficients.Q10) Determine the one sided sequence of

X+(z) = z -n = 7 + 3 z -1 + z -3 + 2 z -4 + 6 z -5

Sign Up