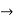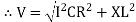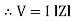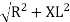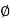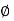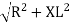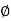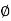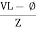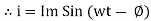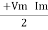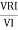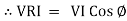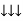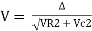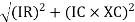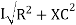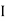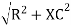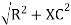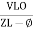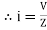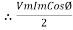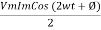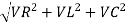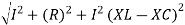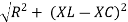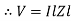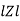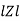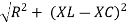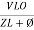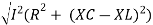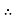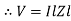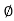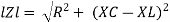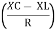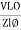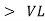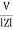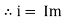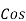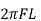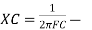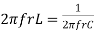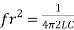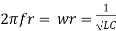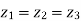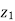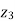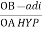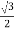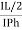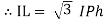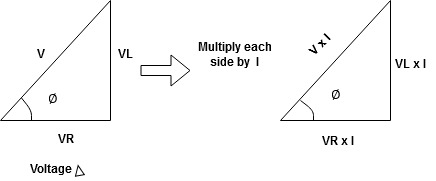
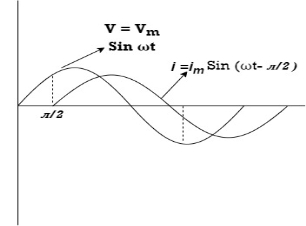
undefined | unit 2 single phase circuit

BEE

UNIT-2Single phase circuit Q1) Explain series R-L circuit?A1)

Consider a series R-L circuit connected across voltage source V= Vm sin wt

Like some, I is the current flowing through the resistor and inductor due do this current-voltage drops across R and L R VR = IR and L VL = I X L

Total V = VR + VL

V = IR + I X L V = I [R + X L]

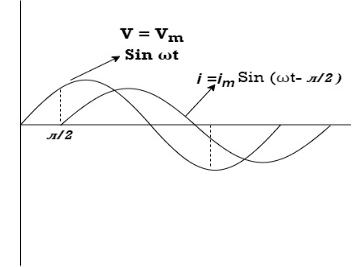
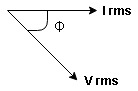
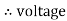Take current as the reference phasor: 1) for resistor current is in phase with voltage 2) for Inductor voltage leads current or current lags voltage by 90 0.

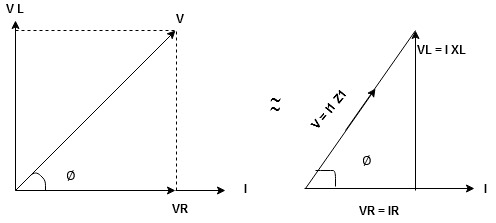
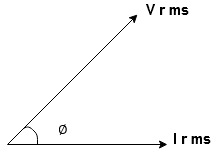
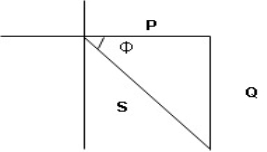
For voltage triangle

Ø is the power factor angle between current and resultant voltage V and

V =

where Z = Impedance of circuit and its value is =

Impedance Triangle Divide voltage triangle by I

Rectangular form of Z = R+ixL

and polar from of Z = L +

(+ j X L + because it is in first quadrant )

Where =

+ Tan -1

Current Equation :

From the voltage triangle, we can sec. that voltage is leading current by or current is legging resultant voltage by

Or i = = [ current angles - Ø )

Resultant Phasor Diagram form Voltage and current eqth.

Waveform

Power equation

P = V .I.

P = Vm Sin wt Im Sin wt – Ø

P = Vm Im (Sin wt) Sin (wt – Ø)

P = (Cos Ø) - Cos (2wt – Ø)

Since 2 sin A Sin B = Cos (A-B) – Cos (A+B)

P = Cos Ø - Cos (2wt – Ø)

①②

Average Power

pang = Cos Ø

Since ② term becomes zero because Integration of cosine come from 0 to 2ƛ

pang = Vrms Irms cos Ø watts.

Power Triangle :

From

VI = VRI + VLI B

Now cos Ø in A =

①

Similarly Sin =

Apparent Power Average or true Reactive or useless power

Or real or active-Unit (VI) Unit (Watts) C/W (VAR) denoted by (Ø)Denoted by [S] denoted by [P] Power

for R L ekt.

Q2) Explain series R-C circuit?A2)

V = Vm sin wt

Consider a series R – C circuit in which resistor R is connected in series with capacitor C across an ac voltage so use V = VM Sin wt (voltage equation).

Assume current I am flowing through

R and C voltage drop across.

R and C R VR = IR

And C Vc = Ic

V = lZl

Voltage triangle: take current as the reference phasor 1) for resistor current is in phase with voltage 2) for capacitor current leads voltage or voltage lags behind current by 900

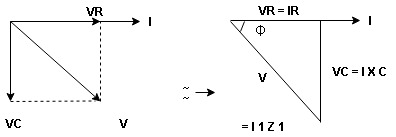
Where Ø is the power factor angle between current and voltage (resultant) V

And from voltage

V =

V = lZl

Where Z = impedance of the circuit and its value is lZl =

Impendence triangle: Divide voltage

as shown

The rectangular form of Z = R - jXc

The polar form of Z = lZl L - Ø

( - Ø and –jXc because it is in the fourth quadrant ) where

lZl =

and Ø = tan -1

Current equation:

from voltage triangle we can see that voltage is lagging current by Ø or current is leading voltage by Ø

i = IM Sin (wt + Ø) since Ø is +ve

Or i = for RC

LØ [ resultant current angle is + Ø]

Resultant phasor diagram from voltage and current equation

Resultant waveform:

Power Equation:

P = V. I

P = Vm sin wt. Im Sin (wt + Ø)

= Vm Im sin wt sin (wt + Ø)

2 Sin A Sin B = Cos (A-B) – Cos (A+B)

Average power

pang = Cos Ø

since 2 terms integration of cosine wave from 0 to 2ƛ become zero

2 terms become zero

pang = Vrms Irms Cos Ø

Power triangle RC Circuit:

Q3) Explain series R-L-C circuit?A3)

Consider ac voltage source V = Vm sin wt connected across the combination of R L and C. when I flowing in the circuit voltage drops across each component as shown below.VR = IR, VL = I

L, VC = I

According to the values of Inductive and Capacitive Reactance, I e XL and XC decides the behaviour of R-L-C series circuit according to following conditions

① XL> XC, ② XC> XL, ③ XL = XC① XL > XC: Since we have assumed XL> XC

The voltage drops across XL> than XC

VL> VC A

Voltage triangle considering condition A

VL and VC are 180 0 out of phase.Therefore, cancel out each other

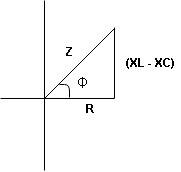
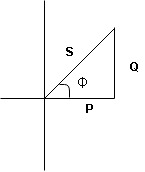
Resultant voltage triangle

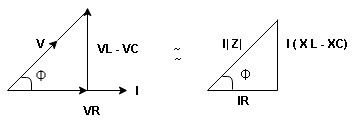
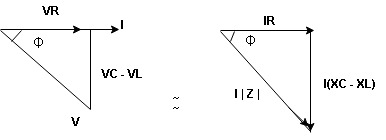
Now V = VR + VL + VC c phasor sum and VL and VC are directly in phase opposition and VLVC their resultant is (VL - VC).

From voltage triangle

V =

V = I

Impendence

: divide voltage

Rectangular form Z = R + j (XL – XC)

Polor form Z = l + Ø B

Where =

And Ø = tan-1

Voltage equation: V = Vm Sin wt
Current equation

i = from B

i = L-Ø C

as VLVC the circuit is mostly inductive and I lags behind V by angle Ø

Since i = L-Ø

i = Im Sin (wt – Ø) from c

XL :Since we have assured XC

the voltage drops across XC

than XL

XL (A)

voltage triangle considering condition (A)

Resultant Voltage

Now V = VR + VL + VC phases sum and VL and VC are directly in phase opposition and VC VL their resultant is (VC – VL)

From voltage

V =

Impedance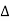

: Divide voltage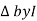

Rectangular form: Z + R – j (XC – XL) – 4th qurd

Polar form : Z = L -

Where

And Ø = tan-1 –

Voltage equation: V = Vm Sin wt
Current equation : i = from B
i = L+Ø C

as VC the circuit is mostly capacitive and leads voltage by angle Ø

since i = L + Ø

Sin (wt – Ø) from C

Power

XL= XC (resonance condition):

ɡȴ XL= XC then VL= VC and they are 1800 out of phase with each other

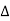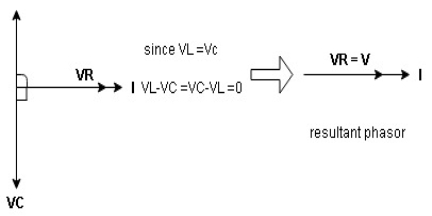
they will cancel out each other and their resultant will have zero value.Hence resultant V = VR and it will be in phase with I as shown in the below phasor diagram.

From the above resultant phasor diagram

V =VR + IR

Or V = I lZl

Because lZl + R

Thus Impedance Z is purely resistive for XL = XC and circuit current will be in phase with source voltage.

Since VR=V Øis zero when XL = XC power is unity

i.e. pang = Vrms I rms cos Ø = 1 cos o = 1

maximum power will be transferred by the condition. XL = XC

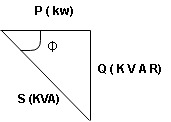
Apparent power: (S): - it is defined as product of rms value of voltage (v) and current (I), or it is the total power/maximum power

S= V × I

Unit - Volte- Ampere (VA)

In kilo – KVA

2. Real power/ True power/Active power/Useful power: (P) it is defined as the product of rms value of voltage and current and the active component or it is the average or actual power consumed by the resistive path (R) in the given combinational circuit.It is measured in watts

P = VI Φ watts / KW, where Φ is the power factor angle.

3. Reactive power/Imaginary/useless power [Q]It is defined as the product of voltage, current and sine B and ITherefore, Q= V.I

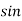ΦUnit –VA RIn kilo- KVAR

As we know power factor is cosine of angle between voltage and current

i.e. Φ.F= CosΦ

In other words, also we can derive it from impedance triangleNow consider Impedance triangle in R.L.ckt

From triangle,

Now Φ – power factor=

Power factor = Φ or

Q4) Explain resonance?A4)It is defined as the phenomenon which takes place in the series or parallel R-L-C circuit which leads to unity power factorVoltage and current in R-L-C ckt are in phase with each other.Resonance is used in many communication circuits such as radio receiver.Resonance in series RLC -> series resonance in parallel->antiresonance/parallel resonance Condition for resonanceXL=XCResonant frequency (fr): For given values R-L-C the inductive reactance XL becomes exactly equal to the capacitive reactance XC only at one particular frequency. This frequency is called as resonant frequency and denoted by ( fr)Expression for resonant frequency (fr)We know that

XL = - inductive reactance

capacitive reactance

At a particle or frequency f=fr,the inductive and capacitive reactance are exactly

Therefore, XL = XC ----at f=fr

i.e.

Therefore,

equal

and rad/sec

Q5) Explain three phase circuit?A5)3Φ system in which three voltages are of identical magnitudes and frequency and are displaced by 120° from each other called as symmetrical system.Phase sequence:The sequence in which the three phases reach their maximum positive values. Sequence is R-Y-B. Three colours used to denote three faces are red, yellow and blue.The direction of rotation of 3Φ machines depends on phase sequence. If a sequence is changed i.e. R-B-Y then the direction of rotation will be reversed.Q6) Explain the types of loads?A6)

Star connection of load

Delta connection of load

Balanced load:Balanced load is that in which magnitudes of all impedances connected in the load are equal and the phase angles of them are also equal.

i.e.

If. ≠ ≠ then it is unbalanced load

Phasor DiagramConsider equation ①Note: we are getting resultant line current IR by subtracting 2 phase currents IRY and IBR

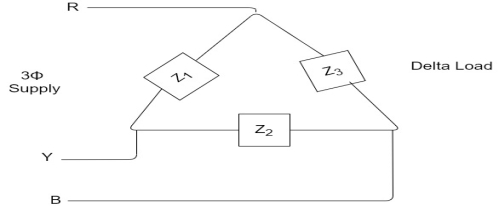
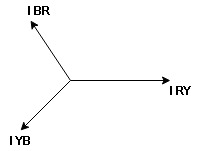
take phase currents at reference as shown

Cos 300 =

Complete phases diagram for delta connected balanced Inductive load.

Phase current IYB lags behind VYB which is phase voltage as the load is inductive Q7) A series RLC circuit containing a resistance of 12Ω, an inductance of 0.15H and a capacitor of 100uF are connected in series across a 100V, 50Hz supply. Calculate the total circuit impedance, the circuits current, power factor and draw the voltage phasor diagram.A7)

Example No1

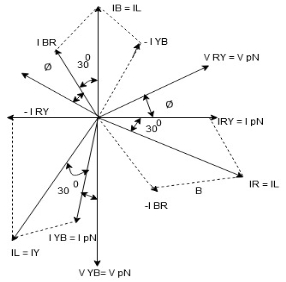
Inductive Reactance, XL.

XL = 2 π f L = 2π x 50 x 0.15 = 47.13 Ω

Capacitive Reactance, XC.

Xc = 1/ 2π fC = 1/ 2π x 50 x 100 x 10 -6 = 31.83 Ω

Circuit Impedance, Z.

Z = [ R 2 + (XL – Xc) 2] ½

Z = [ 12 2 + (47.13 – 31.83) 2] ½

Z = [144 + 234] ½ = 19.4 Ω

Circuits Current, I.

I = Vs/ Z = 100/ 19.4 = 5.14 amps

Voltages across the Series RLC Circuit, VR, VL, VC.

VR = I x R = 5.14 x 12 = 61.7 volts

VL = I x XL = 5.14 x 47.13 = 242.2 volts

Vc = I x Xc = 5.14 x 31.8 = 163.5 volts

Circuits Power factor and Phase Angle, θ.

cos ɸ = R/Z = 12/ 19.4 = 0.619

cos -1 0.619 = 51.8 lagging

Phasor Diagram.

Phasor Diagram

Q8) Find the equivalent resistance in the given circuit diagram (in terms of R)A8)

In order to solve this question, transform the circuit and apply the formula.

Using the formula, we get Ans = 2R/3 Q9) Explain the advantages of series and parallel circuits?A9)

In a series circuit, adding more components to the circuit increases resistance, meaning the electric current decreases.

In a parallel circuit, having additional components does not increase resistance. Resistance can be reduced even further by having more pathways in a parallel circuit.

Q10) Applications of star to delta and delta to star conversions?A10) It is often useful to transform delta network to star and star network to delta while solving an electrical network. The transformation can make the calculations simpler and easier. Some resistor networks cannot be simplified using the usual series and parallel combinations. This situation can often be handled by trying the Δ−Y transformation.

Sign Up