Module-1
Differential calculus-1
Question-1: Find out the angle of intersection of the curves 
Sol.
We eliminate ‘r’ to find the point of intersection of the curves-
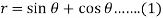
And
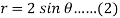
Then-
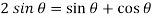
Or
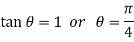
For (1)-
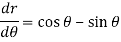
So that-
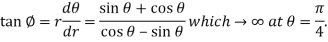
Thus
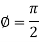
For equation (2)-
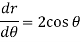
So that-
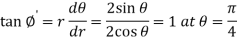
Thus
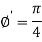
Therefore the angle of intersection of the curves-
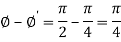
Question-2: Find the pedal equation of the ellipse-
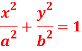
Sol.
Here we have-
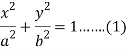
Equation of the tangent at (x, y) is-
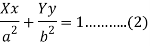
The length of perpendicular ‘p’ from (0, 0) on (2)-
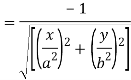
Or
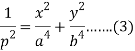
Also-
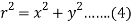
Put the value of 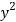 from (4) in (1), we get-
from (4) in (1), we get-
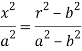
Then from (1)-
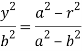
Now put these values of 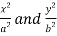 in (3), we get-
in (3), we get-
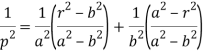
Or
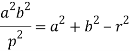
Which is the required pedal equations.
Question-3: Show that for a rectangular hyperbola ,
, 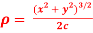 ?
?
Sol.
Given curve 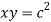 .
.
Differentiating both side with respect to x.
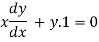
Or  ……(i)
……(i)
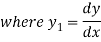
Again differentiating with respect to x.
 using (i)
using (i)
 ….(ii)
….(ii)
The radius of curvature is
Substituting values from (i) and (ii) we get
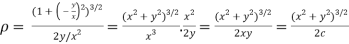 by given curve.
by given curve.
Hence 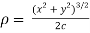 is proved.
is proved.
Question-4: Find the radius of curvature at  of the catenary
of the catenary ?
?
Sol.
Given catenary 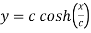 … (i)
… (i)
Differentiating (i) with respect to x.
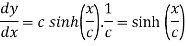
Also consider 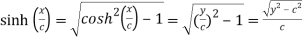
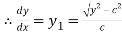 ….. (ii)
….. (ii)
Again differentiating with respect to x , we get
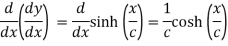
 ….(iii)
….(iii)
The radius of curvature is
Substituting values from (i),(ii) and (iii) we get
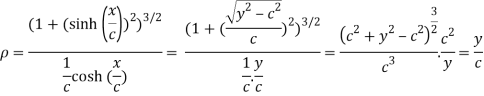
Hence the radius of curvature at  is
is  .
.
Question-5: Find the radius of curvature at the origin for
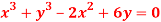
Sol.
Given curve is 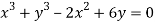 ….(i)
….(i)
Equating lowest degree term to zero we get
 ..(ii)
..(ii)
 Tangent at the origin is on the x-axis.
Tangent at the origin is on the x-axis.
Dividing (i) by y , we get

The radius of curvature at the origin on the x-axis is 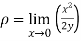 and using (ii)
and using (ii)
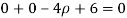
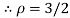 .
.
Question-6: Find the radius of curvature at the origin for-
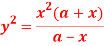
Sol. Given curve 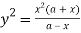
Or 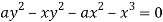 …(i)
…(i)
Equating lowest degree term to zero we get
 ..(ii)
..(ii)
 Tangent at the origin is neither on x-axis nor on y-axis.
Tangent at the origin is neither on x-axis nor on y-axis.
Putting in (i),  where
where 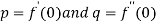 .
.

Where 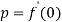
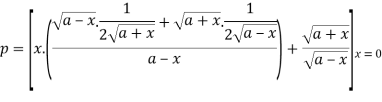
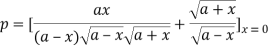
Hence 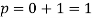
Again 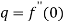
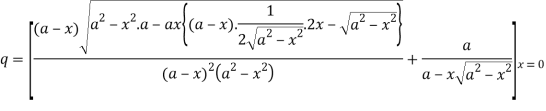
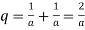 .
.
When the tangent is at the origin and neither on x-axis nor on y-axis then

Substituting the values in p and q we get,
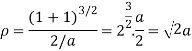
Question-7: Find the coordinates of the centre of curvature at any point of the cycloid-

Sol.
Here we have-
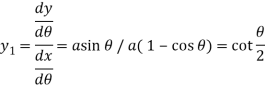
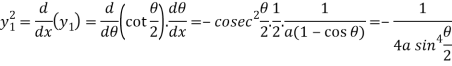
Then centre of curvature-
On putting the above value in formulas, we get-

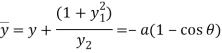
Question-8: Prove that the evolute of parabola 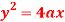 is given by
is given by 
Sol. It is given that-
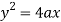
If (X,Y) are the coordinates of the centre of curvature at any point P(x , y) on the curve y = f(x), then X and Y are given as-
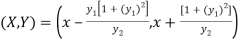 …………….. (1)
…………….. (1)
Now consider the equation of parabola (given)

On differentiating w.r.t x-
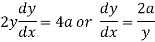
Again differentiating w.r.t.x-
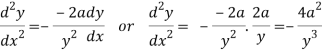
Put these derivatives in (1), we get-
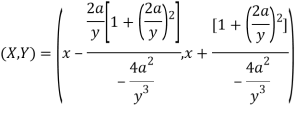
Now consider X,
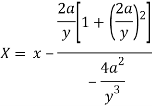
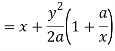
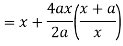
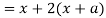
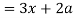
Here we get-
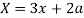
Now consider,
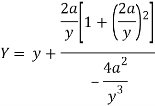
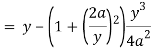
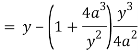
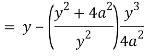
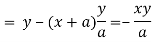
Here we get-

Now
Taking L.H.S of 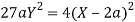
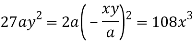
Taking R.H.S of 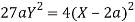
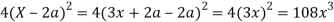
Hence proved.
Question-9: Find the evolute of the ellipse 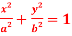 .
.
Sol. It is given that-
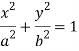
The parametric equations are 
Now,
 and
and
So that-
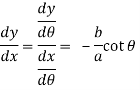
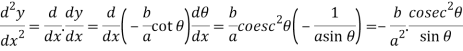
Which gives,
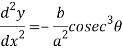
Co-ordinates of centre of curvature are (X , Y),
 …………….. (1)
…………….. (1)
Consider X,
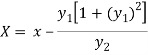


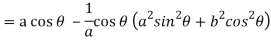
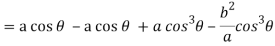
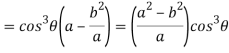
We get-
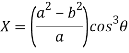
Now consider Y,
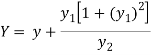

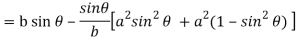
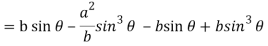
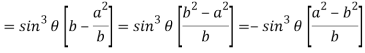
So that we get-
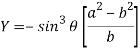
Eliminating 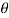 from X and Y, we get,
from X and Y, we get,
 and
and
We know that 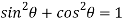
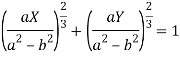
Which gives on solving-

Which is the required evolute.
Question-10: Find the envelope of  , where m is the parameter and A, B and C are function x and y.
, where m is the parameter and A, B and C are function x and y.
Sol. It is given that-
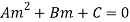 ………………….. (1)
………………….. (1)
Now differentiate equation (1) with respect to ‘m’,
We get-
 , gives
, gives
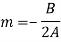
Put these values in equation (1)-


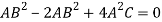
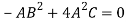
Which gives-
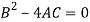
Which is the required envelope.
Module-1
Module-1
Differential calculus-1
Question-1: Find out the angle of intersection of the curves 
Sol.
We eliminate ‘r’ to find the point of intersection of the curves-
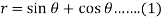
And

Then-

Or
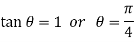
For (1)-
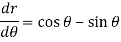
So that-

Thus
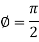
For equation (2)-

So that-
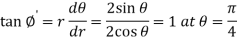
Thus
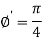
Therefore the angle of intersection of the curves-
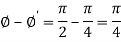
Question-2: Find the pedal equation of the ellipse-
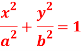
Sol.
Here we have-
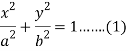
Equation of the tangent at (x, y) is-
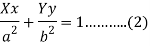
The length of perpendicular ‘p’ from (0, 0) on (2)-
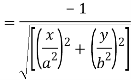
Or
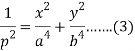
Also-
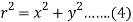
Put the value of  from (4) in (1), we get-
from (4) in (1), we get-
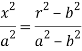
Then from (1)-
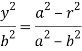
Now put these values of  in (3), we get-
in (3), we get-
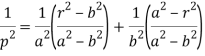
Or
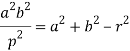
Which is the required pedal equations.
Question-3: Show that for a rectangular hyperbola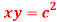 ,
, 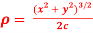 ?
?
Sol.
Given curve 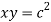 .
.
Differentiating both side with respect to x.
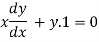
Or  ……(i)
……(i)
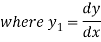
Again differentiating with respect to x.
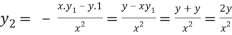 using (i)
using (i)
 ….(ii)
….(ii)
The radius of curvature is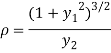
Substituting values from (i) and (ii) we get
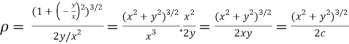 by given curve.
by given curve.
Hence 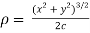 is proved.
is proved.
Question-4: Find the radius of curvature at  of the catenary
of the catenary ?
?
Sol.
Given catenary  … (i)
… (i)
Differentiating (i) with respect to x.
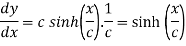
Also consider 
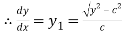 ….. (ii)
….. (ii)
Again differentiating with respect to x , we get
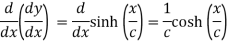
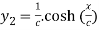 ….(iii)
….(iii)
The radius of curvature is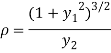
Substituting values from (i),(ii) and (iii) we get
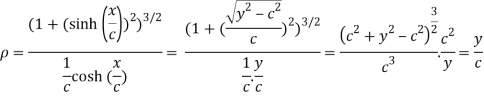
Hence the radius of curvature at  is
is  .
.
Question-5: Find the radius of curvature at the origin for
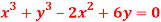
Sol.
Given curve is  ….(i)
….(i)
Equating lowest degree term to zero we get
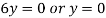 ..(ii)
..(ii)
 Tangent at the origin is on the x-axis.
Tangent at the origin is on the x-axis.
Dividing (i) by y , we get
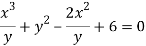
The radius of curvature at the origin on the x-axis is  and using (ii)
and using (ii)
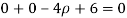
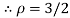 .
.
Question-6: Find the radius of curvature at the origin for-
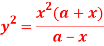
Sol. Given curve 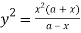
Or 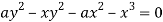 …(i)
…(i)
Equating lowest degree term to zero we get
 ..(ii)
..(ii)
 Tangent at the origin is neither on x-axis nor on y-axis.
Tangent at the origin is neither on x-axis nor on y-axis.
Putting in (i), 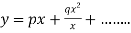 where
where 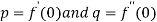 .
.
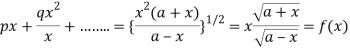
Where 
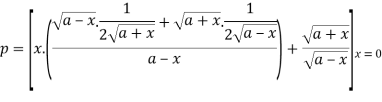
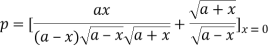
Hence 
Again 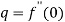
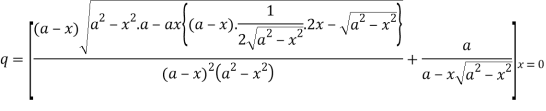
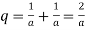 .
.
When the tangent is at the origin and neither on x-axis nor on y-axis then
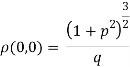
Substituting the values in p and q we get,

Question-7: Find the coordinates of the centre of curvature at any point of the cycloid-

Sol.
Here we have-


Then centre of curvature-
On putting the above value in formulas, we get-
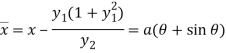
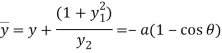
Question-8: Prove that the evolute of parabola 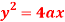 is given by
is given by 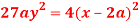
Sol. It is given that-
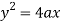
If (X,Y) are the coordinates of the centre of curvature at any point P(x , y) on the curve y = f(x), then X and Y are given as-
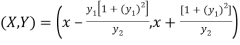 …………….. (1)
…………….. (1)
Now consider the equation of parabola (given)
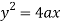
On differentiating w.r.t x-
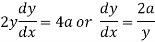
Again differentiating w.r.t.x-
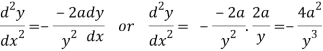
Put these derivatives in (1), we get-

Now consider X,
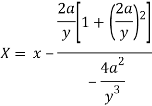


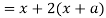
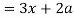
Here we get-
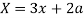
Now consider,
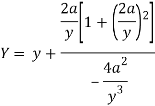
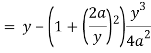
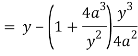
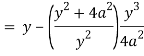
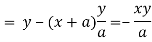
Here we get-
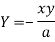
Now
Taking L.H.S of 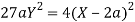
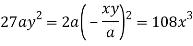
Taking R.H.S of 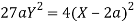

Hence proved.
Question-9: Find the evolute of the ellipse 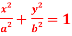 .
.
Sol. It is given that-
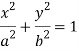
The parametric equations are 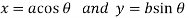
Now,
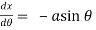 and
and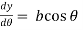
So that-
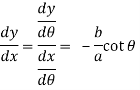

Which gives,

Co-ordinates of centre of curvature are (X , Y),
 …………….. (1)
…………….. (1)
Consider X,
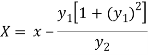
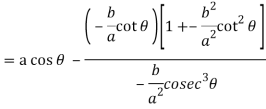
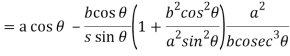
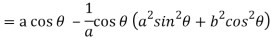
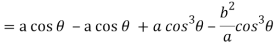
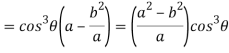
We get-

Now consider Y,
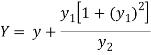
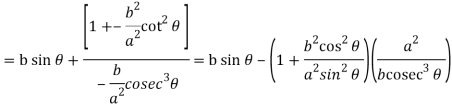
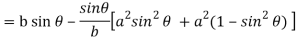
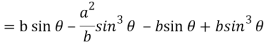
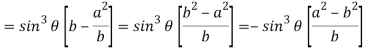
So that we get-
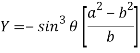
Eliminating 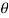 from X and Y, we get,
from X and Y, we get,
 and
and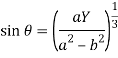
We know that 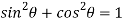
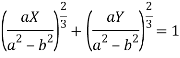
Which gives on solving-
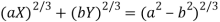
Which is the required evolute.
Question-10: Find the envelope of  , where m is the parameter and A, B and C are function x and y.
, where m is the parameter and A, B and C are function x and y.
Sol. It is given that-
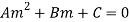 ………………….. (1)
………………….. (1)
Now differentiate equation (1) with respect to ‘m’,
We get-
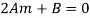 , gives
, gives
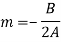
Put these values in equation (1)-
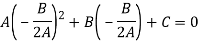
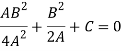
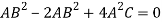
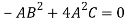
Which gives-

Which is the required envelope.