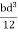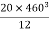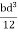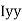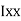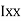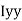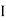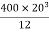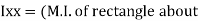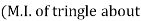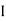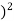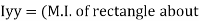undefined | unit 4 centroid

Back to Study material

ECEM

UNIT-4CENTROID Q1) Determine moment of Inertia for

section about x & y axis as shown in figure.

Description: S 25.png

A1)

Consider area ①□ EFGH

M.I. if this rectangle about xx and yy axis will be,

1= =

1 = 162226666.7 mm4

1 = =

1 = 306666.67 mm4

2 = G2

= 106666666.7 mm4

Consider rectangle ABCD area ③

3 = 461066666.7 mm4

3 = 106666666.7 mm4

= 1 + 2 + 3

= 1084.36 106

1 + 2 + 3

= 213.64 106 mm4

Consider rectangle PQMN area ② using parallel axis theorem

2 = G2= A2h22

h22

+ (4002)

2 = 461066666.7 mm4

Q2) Determine the moment of inertia of shaded area as shown in figure about its centroid as axis.A2)

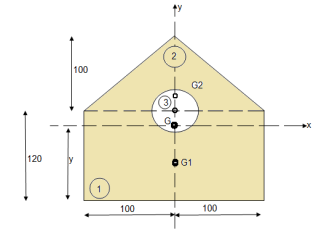
Description: S 26.png

As this figure is symmetrical about

Y axis

X = 100 mm

Y =

There ,

area ① = rectangle

area ② = triangle

area ③ = circle

Y = 79.95 mm

to find M.I. of shaded portion , let G is the centroid of shaded area which is at y = 79.95 mm from base.

of shaded portion @ x-x axis passing through its centroid G will be,

x-x) +

x-x) –

x-x axis)

1 + 23

= (G1 + A1h12) + G2 + A2h22) - G3 + A3h32)

= + -60] +

+ –

84329013.21 mm4

of shaded portion about y-y axis passing through its centroid G will be,

y-y) +

y-y axis) –

y-yaxis)

1 + 23

= 80000000 + 16666666.67 – 3220623.34

93446043.33 mm4

Q3) Find the support reactions of given beam for loading as shown below.

A3)

Draw FBD of given beam & applying conditions of equilibrium

∑fx = 0RHA = 0∑fxy= 0RVA – 20 + RB = 0RVA + RB = 20 ------(1)Taking moments at A∑MA = 0(20 × 3) – (RB × 5) = 060 – 5RB

RB = 12 kN

put in equation (1)

RVA + 12 = 20

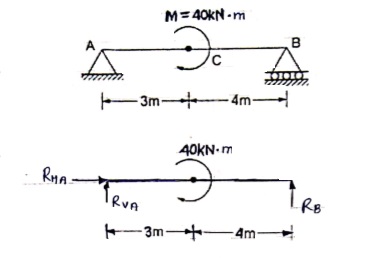
RVA = 20-12RVA = 8 kN

Q4) Find support reaction for given beam .

A4)

Resolving forces horizontally∑fx = 0RHA = 0 Resolving forces vertically∑fy= 0RVA – 60 + RB = 0RVA + RB = 60 ------- (1)Taking moment at A∑MA = 0(60 × 2) – (RB × 4 ) = 0

120 – 4RB = 0

RB =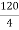

RB = 30 kN

Q5) Find the support reactions of a given loading for Beam.

A5)

Resolving forces horizontally∑fX = 0RHA = 0Resolving forces vertically ∑fY= 0RVA – 60 + RB = 0RVA + RB = 60 ----------------- (1) Taking moments at A∑ MA = 0(RVA × 0) + (60 × 2.67) – 4RB = 0160.2 – 4RB = 0

put in equation (1)We get RVA + 40 = 60RVA = 60 – 40RVA = 20 kN

Q6) Find the support reactions for given beam.

A6)

Resolving force horizontally∑fX = 0RHA = 0 Resolving forces vertically∑fy = 0RVA + RB = 0 ------- (1)Taking moments at A

40 – 7RB = 0

RB =

RB = 5.71 kN

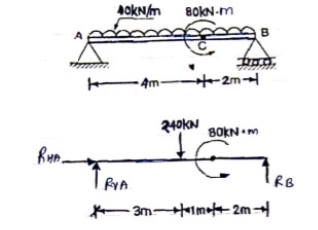
Put above value in equation (1)RVA + RB = 0RVA + 5.71 = 0 RVA = - 5.71 kNRVA = 5.71 kN

Q7)

A7)Resolving forces horizontally∑fX = 0RHA = 0Resolving forces vertically∑fy = 0RVA – 240 + RB = 0RVA + RB = 240 ----------- (1)Taking moment at A∑ MA = 0(240 × 3) – 80 – 6RB = 0640 – 6RB = 0RB = 106.67 kN

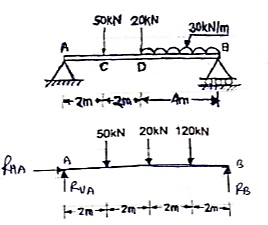
Put this value in equation (1)RVA + RB = 240RVA = 240 – 106.67RVA = 133.33 kN

Q8) Find support reactions for the loading as shown below:

A8)

Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 ---- (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN

Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN

Q9) Find the reactions at support A & B.

A9)

Resolving forces vertically∑fy = 0RVA – 30 – 80 + RB = 0RVA + RB = 110 ------ (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 018 + 373.6 – 6RB = 06RB = 391.6RB= 65.267 kNPut above value in equation (1)RVA + RB = 110RVA + 65.267 = 110RVA = 110 – 65.267RVA = 44.733 KN Q10) Find support reactions at A & B

A10)

Resolving forces vertically∑fy = 0RVA – 8 – 18 – 5 – 20 + RB = 0RVA + RB = 51 ------ (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(8 × 2) + (18 × 3.5) + (5 × 5 ) + (20 × 8.67) – 10RB = 016+ 63 + 25 + 173.4 – 10RB = 0277.4 – 10RB = 0RB = 27.74 kNPut above value in equation (1)RVA = 51 – 27.74RVA = 23.26 kN Q11) Explain the difference between centre of gravity and centroid?A11)

Difference Between Center of Gravity and Centroid
Center of Gravity	Centroid
The point where the total weight of the body focuses upon	It is referred to the geometrical center of a body
It is the point where the gravitational force (weight) acts on the body	It is referred to the center of gravity of uniform density objects
It is denoted by g	It is denoted by c
Center of Gravity in a uniform gravitational field is the average of all points, weighted by local density or specific weight	The centroid is a point in a plane area in such a way that the moment of area about any axis throughout that point is 0
It is a physical behaviour of the object, a point where all the weight of an object is acting	It is a geometrical behaviour. It is the center of measure of the amount of geometry.

Q12) Find the centroid of the triangle whose vertices are A(2, 6), B(4, 9), and C(6,15).A12)Given:A(x1, y1) = A (2, 6)B(x2, y2) = B (4, 9)C(x3, y3) = C (6, 15)We know that the formula to find the centroid of a triangle is = ((x1+x2+x3)/3, (y1+y2+y3)/3)Now, substitute the given values in the formulaCentroid of a triangle = ((2+4+6)/3, (6+9+15)/3)= (12/3, 30/3)= (4, 10)Therefore, the centroid of the triangle for the given vertices A(2, 6), B(4,9), and C(6,15) is (4, 10).

Sign Up