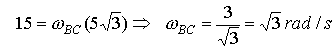ECEM
UNIT-5KINEMATICS Q1) Find INSTANTANEOUS CENTER OF VELOCITY?
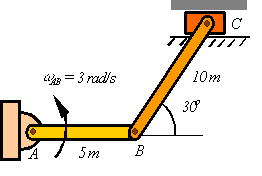
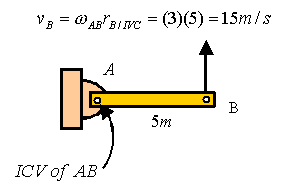
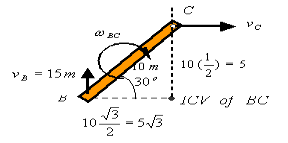
Given that bar AB rotates with an angular velocity of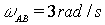 
calculate the angular velocity of BC and the velocity of C. A1) Bar AB:
Bar BC:
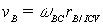
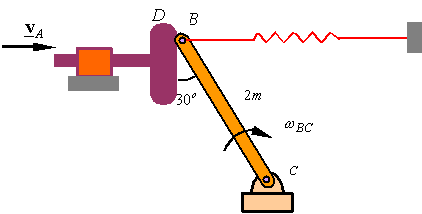
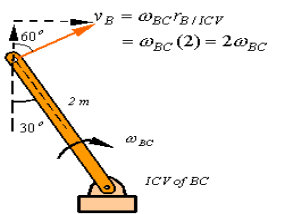
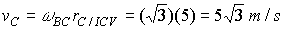Q2) Find INSTANTANEOUS CENTER OF VELOCITY? A2) Given that VA=10m/s calculate the angular velocity of BC. Assume that B is in contact with D at all times.
First find velocity of B Using the bar BC. The non-penetration condition requires that the horizontal component of the velocity of B be equal to the horizontal component of velocity of D, therefore,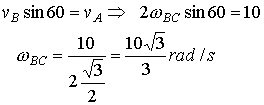 
Q3) Instantaneous canters of a kinematic chain?A3) Instantaneous center is a point in common between two members where the velocities are equal, both in direction and magnitude. The number of instantaneous centers in a considered kinematic chain is equal to number of combinations of two links: If N is the number of instantaneous centers and n is the number of links. N = n (n-1)/2There are neither three types of instantaneous centers namely fixed, permanent and neither fixed nor permanent. The first two types are together known as primary instantaneous centers and the third type is known as secondary instantaneous centers.Q4) Explain the properties of the instantaneous centre?A4)1. A rigid link rotates instantaneously relative to another link at the instantaneous centre for the configuration of the mechanism considered.2. The two rigid links have no linear velocity relative to each other at the instantaneous centre. At this point (i.e. instantaneous centre), the two rigid links have the same linear velocity relative to the third rigid link. In other words, the velocity of the instantaneous centre relative to any third rigid link will be same whether the instantaneous centre is regarded as a point on the first rigid link or on the second rigid link.Q5) the velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line?A5) A link is rotating about O. Velocity of point P on link w.r.t. point Q on link will be perpendicular to PQ.The velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line joining the corresponding points.Q6) there are two points P and Q on a planar rigid body. The relative velocity between the two points?A6) Explanation: Velocity of any point on a link with respect to another point (relative velocity) on the same link is always perpendicular to the line joining these points on the configuration (or space) diagram.vQP = Relative velocity between P & Q
= vP −vQ always perpendicular to PQ. Q7) The number of inversion for a slider crank mechanism is?A7) For a 4 bar slider crank mechanism, there are the numbers of links or inversions are 4. These different inversions are obtained by fixing different links once at a time for one inversion. Hence, the number of inversions for a slider crank mechanism is 4. Q8) Explain Grashof’s law ?A8) Here P, Q, R, & S are the lengths of the links.In a four-bar linkage, S denotes the shortest link length, L is the longest link length, P and Q are the lengths of other two links. At least one of the three moving links will rotate by 3600According to Grashof’s law : “For a four bar mechanism, the sum of the shortest and longest link lengths should not be greater than the sum of remaining two link lengths, if there is to be continuous relative motion between the two linksS + L < P +QQ9) Explain Kutzbach criterion?A9) From the Kutzbach criterion the degree of freedomn = 3(l − 1) − 2j − hThe minimum number of links in a single degree-of-freedom planar mechanism with both higher and lower kinematic pairs isFor single degree of Freedom (n = 1),
1 = 3(l − 1) − 2j − h
3l − 2j − 4 − h = 0 …(i)
The simplest possible mechanisms of single degree of freedom is four-bar mechanism. For this mechanism j = 4, h = 0
From equation (i), we have3l − 2 x 4 − 4 − 0 = 0
or, l = 4Q10) A man walks 500 m due east in 300 s followed by 400 m due west in 320 s. Determine:A) his average velocity for i) 500 m, ii) 400 m
B) his average velocity for the whole journeyA10) Consider the direction east to be positive and the direction west to be negative. Therefore there will be no need to write the directions for distance and velocity as these will be shown as positive or negative numbers.A) i) for 500 m: v = 500/300
v = 1.67 m/sii) For 400m: v = -400/320
v = -1.25 m/sB) The actual distance travelled in a particular direction in 620 seconds (300+320) is 500 + (-400) = 100 m in an easterly direction.Although the man has walked a total distance of 900 m, he has effectively only walked 100 m east because he changed direction in the lat 400 m.Therefore the actual distance travelled in a particular direction is called a displacement.
And the average velocity of the man = 100/(300 + 320)
= 0.16 m/sNote that the average speed of the man will be:
900/620 = 1.45 m/s as the man has still walked 900 m in 620 s.
| |
|
|
|
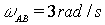calculate the angular velocity of BC and the velocity of C. A1) Bar AB:
| |
|
|
|
|
| |
|
|
|
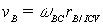
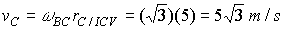Q2) Find INSTANTANEOUS CENTER OF VELOCITY? A2) Given that VA=10m/s calculate the angular velocity of BC. Assume that B is in contact with D at all times.
| |
|
|
|
|
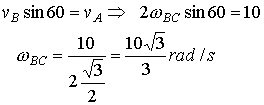Q3) Instantaneous canters of a kinematic chain?A3) Instantaneous center is a point in common between two members where the velocities are equal, both in direction and magnitude. The number of instantaneous centers in a considered kinematic chain is equal to number of combinations of two links: If N is the number of instantaneous centers and n is the number of links. N = n (n-1)/2There are neither three types of instantaneous centers namely fixed, permanent and neither fixed nor permanent. The first two types are together known as primary instantaneous centers and the third type is known as secondary instantaneous centers.Q4) Explain the properties of the instantaneous centre?A4)1. A rigid link rotates instantaneously relative to another link at the instantaneous centre for the configuration of the mechanism considered.2. The two rigid links have no linear velocity relative to each other at the instantaneous centre. At this point (i.e. instantaneous centre), the two rigid links have the same linear velocity relative to the third rigid link. In other words, the velocity of the instantaneous centre relative to any third rigid link will be same whether the instantaneous centre is regarded as a point on the first rigid link or on the second rigid link.Q5) the velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line?A5) A link is rotating about O. Velocity of point P on link w.r.t. point Q on link will be perpendicular to PQ.The velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line joining the corresponding points.Q6) there are two points P and Q on a planar rigid body. The relative velocity between the two points?A6) Explanation: Velocity of any point on a link with respect to another point (relative velocity) on the same link is always perpendicular to the line joining these points on the configuration (or space) diagram.vQP = Relative velocity between P & Q= vP −vQ always perpendicular to PQ. Q7) The number of inversion for a slider crank mechanism is?A7) For a 4 bar slider crank mechanism, there are the numbers of links or inversions are 4. These different inversions are obtained by fixing different links once at a time for one inversion. Hence, the number of inversions for a slider crank mechanism is 4. Q8) Explain Grashof’s law ?A8) Here P, Q, R, & S are the lengths of the links.In a four-bar linkage, S denotes the shortest link length, L is the longest link length, P and Q are the lengths of other two links. At least one of the three moving links will rotate by 3600According to Grashof’s law : “For a four bar mechanism, the sum of the shortest and longest link lengths should not be greater than the sum of remaining two link lengths, if there is to be continuous relative motion between the two linksS + L < P +QQ9) Explain Kutzbach criterion?A9) From the Kutzbach criterion the degree of freedomn = 3(l − 1) − 2j − hThe minimum number of links in a single degree-of-freedom planar mechanism with both higher and lower kinematic pairs isFor single degree of Freedom (n = 1),
1 = 3(l − 1) − 2j − h
3l − 2j − 4 − h = 0 …(i)
The simplest possible mechanisms of single degree of freedom is four-bar mechanism. For this mechanism j = 4, h = 0
From equation (i), we have3l − 2 x 4 − 4 − 0 = 0
or, l = 4Q10) A man walks 500 m due east in 300 s followed by 400 m due west in 320 s. Determine:A) his average velocity for i) 500 m, ii) 400 m
B) his average velocity for the whole journeyA10) Consider the direction east to be positive and the direction west to be negative. Therefore there will be no need to write the directions for distance and velocity as these will be shown as positive or negative numbers.A) i) for 500 m: v = 500/300
v = 1.67 m/sii) For 400m: v = -400/320
v = -1.25 m/sB) The actual distance travelled in a particular direction in 620 seconds (300+320) is 500 + (-400) = 100 m in an easterly direction.Although the man has walked a total distance of 900 m, he has effectively only walked 100 m east because he changed direction in the lat 400 m.Therefore the actual distance travelled in a particular direction is called a displacement.
And the average velocity of the man = 100/(300 + 320)
= 0.16 m/sNote that the average speed of the man will be:
900/620 = 1.45 m/s as the man has still walked 900 m in 620 s.
0 matching results found