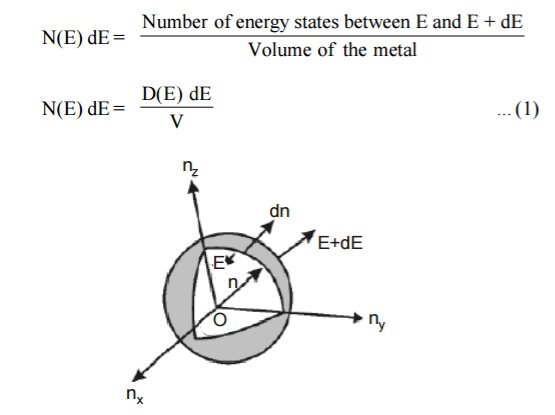
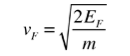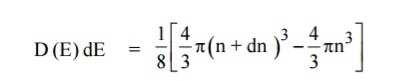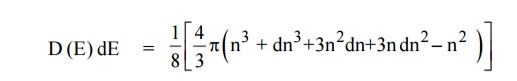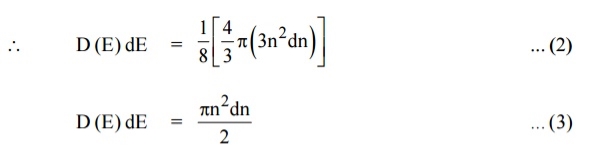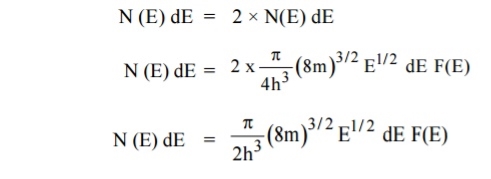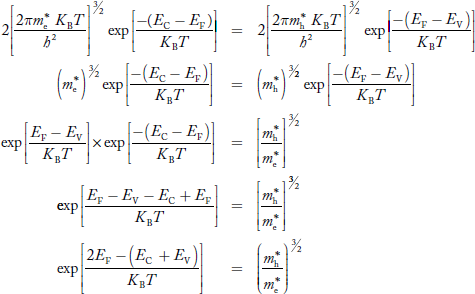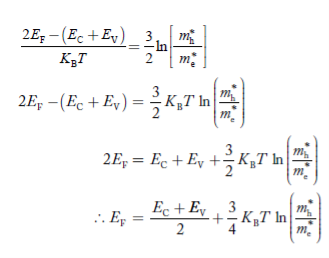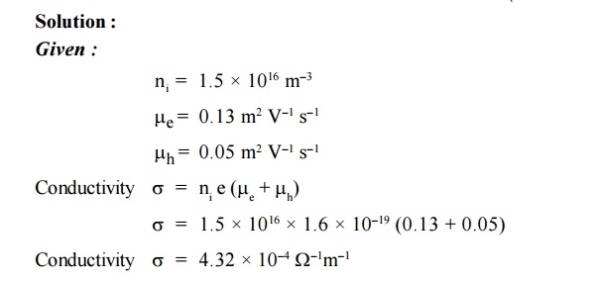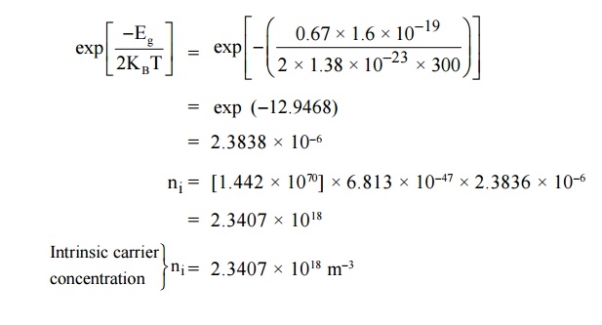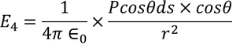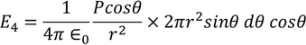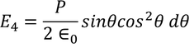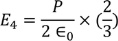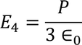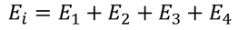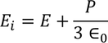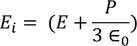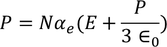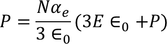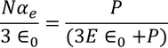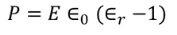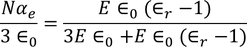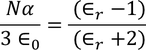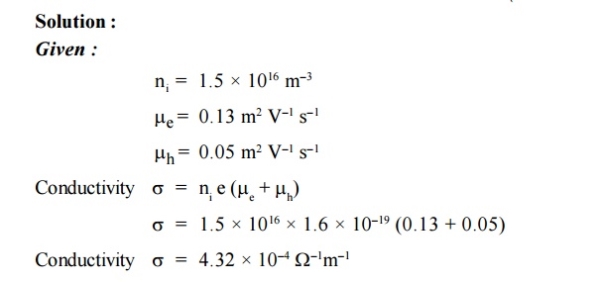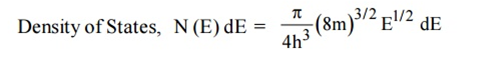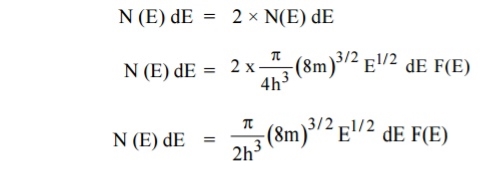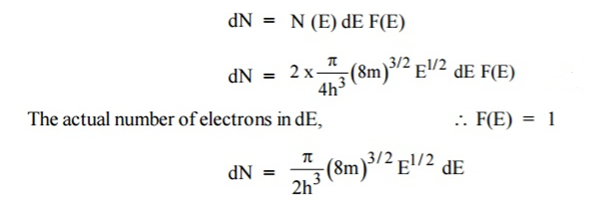undefined | unit 5 material science

PHY

UNIT 5MATERIAL SCIENCE Q1) Write the Similarities and Differences between Classical Free Electron Theory and Quantum Free Electron Theory?A1) Similarities between the two theories The following assumptions apply to both the theories:

The valence electrons are treated as though they constitute an ideal gas.

The valence electrons can move freely throughout the body of the solid.

The mutual repulsion between the electrons, and the force of attraction between the electrons and ions are considered insignificant.

Difference between the two theories

Classical Free Electron Theory	Quantum Free Electron Theory
The free electrons, which constitute the electron gas can have continuous energy values.	The energy values of the free electrons are discontinuous because of which the energy levels are discrete.
2. It is possible that many electron may possess same energy.	2. The free-electrons obey the Pauli exclusion principle. Hence no two electrons can possess same energy.
3. The pattern of distribution of energy among the free electron obey Maxwell-Boltzmann statistics.	3. The distribution of energy among the free electrons is according to Fermi Dirac statistics which imposes a severe restriction on the possible way in which the electrons absorb energy from an external source.

Q2) Give Assumptions of classical free electron theory?A2) The classical free electron theory is based on the following postulates. 1. The valence electrons of atoms are free to move about the whole volume of the metal, like the molecules of a perfect gas in a container. 2. The free electrons move in random direction and collide with either positive ions fixed to the lattice or the other free electrons. All the collisions are elastic in nature i.e., there is no loss of energy. 3. The momentum of free electrons obeys the laws of the classical kinetic theory of gases. 4. The electron velocities in a metal obey classical Maxwell-Boltzman distribution of velocities. 5. When the electric field is applied to the metal, the free electrons are accelerated in the direction opposite to the direction of applied electric field. 6. The mutual repulsion among the electrons is ignored, so that they move in all the directions with all possible velocities. 7. In the absence of the field, the energy associated with an electron at temperature T is given by

kT. It is related to the kinetic energy equation

kT =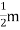

v2thHere vth represents the thermal velocity. Q3) Write Success and failure of classical free electron theory?A3) Success of classical free electron theory1. It verifies ohm’s law 2. It explains electrical conductivity of metals. 3. It explains thermal conductivity of metals. 4. It derives Widemann – Franz law. (i.e. the relation between electrical and thermal conductivity. Draw backs of classical free electron theory. 1. It could not explain the photoelectric effect, Compton Effect and black body radiation. 2. Electrical conductivity of semiconductors and insulators could not be explained. 3. Widemann – Franz law (K/σT= constant) is not applicable at lower temperatures. 4. Ferromagnetism could not be explained by this theory. The theoretical value of paramagnetic susceptibility is greater than the experimental value. 5. According to classical free electron theory the specific heat of metals is given by 4.5R whereas the experimental value is given by 3R. 6. According to classical free electron the electronic specific heat is equal to 3/2R while the actual value is 0.01R.Q4) Derive expression for Electrical Conductivity according to free electron theory and also discuss its temperature dependence?A4) The classical free electron theory was proposed by Drude and Lorentz. According to this theory the electrons are moving freely and randomly moving in the entire volume of the metal like gas atoms in the gas container. When an electric field is applied the free electrons gets accelerated. When an electric field E is applied between the two ends of a metal of area of cross section A When an electrical field (E) is applied to an electron of charge ‘e’ of a metallic rod, the electron moves in opposite direction to the applied field with a velocity vd. This velocity is known as drift velocity. Drift velocity vd is defined as the average velocity of the free electrons with which they move towards the positive terminal under the influence of the electrical field. Lorentz force acting on the electron F = eE ........(1) This force is known as the driving force of the electron.Due to this force, the electron gains acceleration ‘a’. From Newton’s second law of motion, Force F = ma …....(2) From the equation (1) and (2),ma = eE or a =

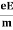…......(3)Acceleration (a) =

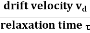Or a =

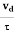Relaxation time is defined as the time taken by a free electron to reach its equilibrium position from the disturbed position in the presence of an electric field.So vd = a ……….(4)Substituting equation (3) in (4)vd =

 =

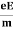E ……….(5)vd =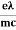

E ……….(5a)Where

= RMS velocityThe Ohms’ law states that current density (J) is expressed as J =E ……….(6)Or  =

Where  is the electrical conductivity of the electron. But, the current density in terms of drift velocity is given as J = nevd ....... (7)Substituting equation (5) in equation (7), we haveJ = ne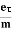

E Or

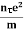On comparing the equation (6) and (8) , we haveElectrical conductivity  =

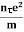....... (8) =

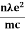....... (8a)This is a required expression for electrical conductivity.Resistivity ρρ =

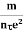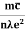According to kinetic theory of gasses

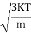So  =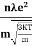

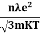Alsoρ =

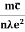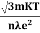Mobility: It is defined as the drift velocity of the charge carrier per unit applied electric field.μ=

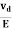....... (9)From equation (7) we have J = nevdby substituting vd =μEfrom equation (9)J = neμEOr

= μne ....... (10)We know by ohms law =

so equation (10) can be rewritten as= μneμ =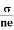

This is the required expression for mobility.Temperature dependenceThe positive ions are always in oscillating (or vibrating) state about their mean position; even the substance is present at 0k temperature. The vibrating amplitude of ions is always depends the temperature. The mean free path λ of the electrons is inversely proportional to the mean square of amplitude of ionic vibrations A0λ =

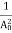………(1) The energy of lattice vibrations is proportional to

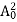and increases linearly with temperature T.

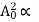T ……….(2) From equations (1) and (2)λ =

………..(3) The resistivity ρ of the metal is inversely proportional to mean free path of electrons λρ =

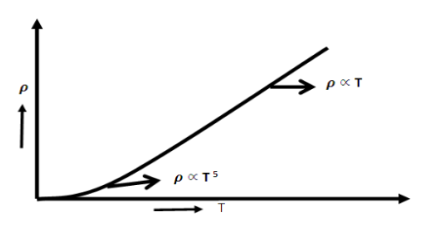
..…………..(4) From equations (3) and (4)ρ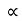

T ..……….(5) From equation (5) we observe that the resistivity of metal is linearly increases with temperature. The conductivity  is defined as the reciprocal of resistance. 

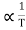………….(6) From equation (6) we observe that the conductivity of metal is inversely proportional to their temperature. The variation of resistivity of metal with temperature is shown in figure.

Figure 1: Variation of resistivity of metal with temperatureQ5) Derive hall coefficient? Show how hall coefficient and mobility are related? A5) When magnetic field is applied perpendicular to a current-carrying conductor, then a voltage is developed in the material perpendicular to both magnetic field and current in the conductor. This effect is known as Hall Effect and the voltage developed is known as Hall voltage (VH). Hall Effect is useful to identify the nature of charge carriers in a material and hence to decide whether the material is n-type semiconductor or p-type semiconductor, also to calculate carrier concentration and mobility of carriers.Hall Effect can be explained by considering a rectangular block of an extrinsic semiconductor in which current is flowing along the positive X-direction and magnetic field B is applied along Z-direction as shown in Figure.

Figure 12: Hall EffectSuppose if the semiconductor is n-type, then mostly the carriers are electrons and the electric current is due to the drifting of electrons along negative X-direction or if the semiconductor is p-type, then mostly the carriers are holes and the electric current is due to drifting of the holes along positive X-direction. As these carriers are moving in magnetic field in the semiconductor that mean they experience Lorentz force represented by FLFL = Bevd Where vd is the drift velocity of the carriers. (already explained in previous section).We can obtain the direction of this force by applying Fleming’s left-hand rule in electromagnetism.Fleming’s left-hand rule can be explained as If we stretch the thumb, fore finger and middle finger in three perpendicular directions so that the fore finger is parallel to the magnetic field and the middle finger is parallel to the current direction, then thumb represents the direction of force on the current-carrying carriers. So the Lorentz force is exerted on the carriers in the negative Y-direction. Due to Lorentz force, more and more carriers will be deposited at the bottom face (represented by face 1in figure) of the conductor. The deposition of carriers at the bottom face is continued till the repulsive force due to accumulated charge balances the Lorentz force. After some time of the applied voltage, both the forces become equal in magnitude and act in opposite direction, then the potential difference between the top and bottom faces is equal to Hall voltage and that can be measured.At equilibrium, the Lorentz force on a carrier FL = Bevd ……………..(1)and the Hall force FH = eEH ……………..(2)Where EH is the Hall electric field due to accumulated charge.At equilibrium, FH = FLeEH = Bevd∴ EH = Bvd ……………..(3)If ‘d’ is the distance between the upper and lower surfaces of the slab, then the Hall fieldEH =

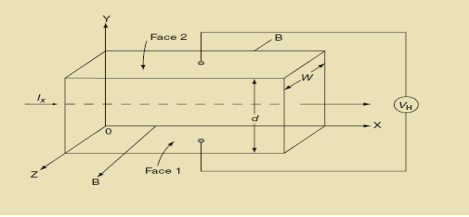
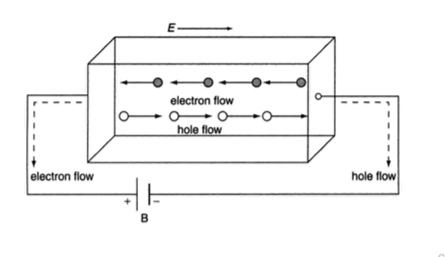
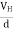……………..(4)In n-type material, Jx = –nevdvd = -

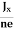……………..(5)Where n is free electron concentration, substituting (5) in (3), we have∴ EH = -B

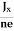……………..(6)For a given semiconductor, the Hall field EH is proportional to the current density Jx and the intensity of magnetic field ‘B’ in the material.i.e. EH ∝ JxB(or) EH = RHJxB ……………..(7)Where RH = Hall coefficientEquations (6) and (7) are same so, we haveRHJxB =-B

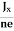RH = -

= -

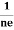……………..(8)Where ρ is charge density Similarly for p-type materialRH =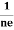

……………..(9)Using Equations (8) and (9), carrier concentration can be determined.Thus, the Hall coefficient is negative for n-type material. In n-type material, as more negative charge is deposited at the bottom surface, so the top face acquires positive polarity and the Hall field is along negative Y-direction. The polarity at the top and bottom faces can be measured by applying probes. Similarly, in case of p-type material, more positive charge is deposited at the bottom surface. So, the top face acquires negative polarity and the Hall field is along positive Y-direction. Thus, the sign of Hall coefficient decides the nature of (n-type or p-type) material. The Hall coefficient can be determined experimentally in the following way:Multiplying Equation (7) with ‘d’, we haveEHd = VH = RHJxBd ……………..(10)From (Figure 11) we know the current density JxJx =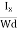

Where W is width of the box. Then, Equation (10) becomesVH = RH

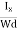Bd = RH

RH =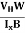

……………..(11)Substituting the measured values of VH, Ix, B and W in Equation(11), RH is obtained. The polarity of VH will be opposite for n- and p-type semiconductors.The mobility of charge carriers can be found by using the Hall effect, for example, the conductivity of electrons isn= neμnOr we can rewrite it asμn =

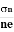=n RH ……………..(12)by using equation (11)μn = n

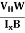……………..(13) Q6) Explain the term Fermi level and Fermi energy?A6) Fermi level" is the term used to describe the top of the collection of electron energy levels at absolute zero temperature. This concept comes from Fermi-Dirac statistics. Electrons are fermions and by the Pauli Exclusion Principle cannot exist in identical energy states. So at absolute zero they pack into the lowest available energy states and build up a "Fermi sea" of electron energy states. The Fermi level is the surface of that sea at absolute zero where no electrons will have enough energy to rise above the surface. The concept of the Fermi energy is a crucially important concept for the understanding of the electrical and thermal properties of solids. Both ordinary electrical and thermal processes involve energies of a small fraction of an electron volt. But the Fermi energies of metals are on the order of electron volts. This implies that the vast majority of the electrons cannot receive energy from those processes because there are no available energy states for them to go to within a fraction of an electron volt of their present energy. Limited to a tiny depth of energy, these interactions are limited to "ripples on the Fermi sea". At higher temperatures a certain fraction, characterized by the Fermi function, will exist above the Fermi level. The Fermi level plays an important role in the band theory of solids. In doped semiconductors, p-type and n-type, the Fermi level is shifted by the impurities, illustrated by their band gaps. The Fermi level is referred to as the electron chemical potential in other contexts.

In metals, the Fermi energy gives us information about the velocities of the electrons which participate in ordinary electrical conduction. The amount of energy which can be given to an electron in such conduction processes is on the order of micro-electron volts (see copper wire example), so only those electrons very close to the Fermi energy can participate. The Fermi velocity of these conduction electrons can be calculated from the Fermi energy.

This speed is a part of the microscopic Ohm's Law for electrical conduction. For a metal, the density of conduction electrons can be implied from the Fermi energy.

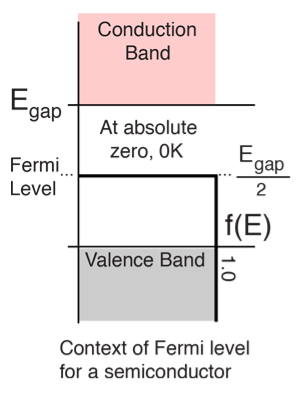
Figure 4: Fermi level for a Semiconductor

The Fermi energy also plays an important role in understanding the mystery of why electrons do not contribute significantly to the specific heat of solids at ordinary temperatures, while they are dominant contributors to thermal conductivity and electrical conductivity. Since only a tiny fraction of the electrons in a metal are within the thermal energy kT of the Fermi energy, they are "frozen out" of the heat capacity by the Pauli principle. At very low temperatures, the electron specific heat becomes significant.It is named after the Physicist Enrico Fermi. A Fermi level is the measure of the energy of least tightly held electrons within a solid. It is important in determining the thermal and electrical properties of solids. It can be defined as:The Fermi energy is a concept in quantum mechanics usually refers to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.The value of the Fermi level at absolute zero temperature is known as the Fermi energy. It is also the maximum kinetic energy an electron can attain at 0K. Fermi energy is constant for each solid.To determine the lowest possible Fermi energy of a system, we first group the states with equal energy into sets and arrange them in increasing order of energy. We then add particles one at a time, successively filling up the unoccupied quantum states with the lowest energy.When all the particles are arranged accordingly, the energy of the highest occupied state is the Fermi energy. In Spite of the extraction of all possible energy from metal by cooling it to near absolute zero temperature (0 Kelvin), the electrons in the metal still move around. The fastest ones move at a velocity corresponding to a kinetic energy equal to the Fermi energy.The highest energy level that an electron can occupy at the absolute zero temperature is known as the Fermi Level. The Fermi level lies between the valence band and conduction band because at absolute zero temperature the electrons are all in the lowest energy state. Due to lack of sufficient energy at 0 Kelvin, the Fermi level can be considered as the sea of fermions (or electrons) above which no electrons exist. The Fermi level changes as the solids are warmed and as electrons are added to or withdrawn from the solid. Don’t get confuse between Fermi level and Fermi energy.Both the terms are equal at absolute zero temperature but they are different at other temperature.Q7) Define Fermi function also discuss effect of temperature on Fermi function?A7) Fermi function F (E):Fermi-Dirac distribution function represents the probability of an electron occupying a given energy level at absolute temperature. It is given by

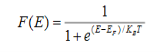Where KB Boltzmann Constant T Temperature If g(E) is the density of states and f(E) gives the probability of occupation of those states at a given temperature, the number of occupied states, n(E),is given by n(E) =

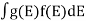(1) If the number of occupied states in an energy band needs to be calculated the integration needs to be performed over the entire band. This will be a function of temperature, since the Fermi function is temperature dependent. Equation 1 can be used to calculate the concentration of electron and holes in semiconductors, which decides their conductivity.Effect of temperature on Fermi Function:Case (i) Probability of occupation for E < EF at T = 0K

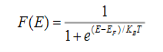When T = 0K and E < EF, we haveF(E) =

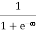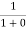= 1Thus at T = 0K, there is 100 % chance for the electrons to occupy the energy levels below the Fermi level.

Figure 3: Fermi distributionCase (ii) Probability of occupation for E>EF at T = 0K When T = 0K and E > EF, we have F(E) =

= 0Thus, there is 0 % chance for the electrons to occupy energy levels above the Fermi energy level. From the above two cases, at T = 0K the variation of F(E) for different energy values becomes a step function.Case (iii) Probability of occupation at ordinary temperatureAt ordinary temperature, the value of probability starts reducing from 1 for values of E slightly less than EF. With the increase of temperature, i.e., T> 0K, Fermi function F (E) varies with E. At any temperature other than 0K and E = EFF(E) =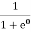

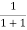= 50%Hence, there is 50 % chance for the electrons to occupy Fermi level. Further, for E > EF the probability value falls off rapidly to zero. Case (iv) At high temperatureWhen kT >> EF, the electrons lose their quantum mechanical character and Fermi distribution function reduces to classical Boltzmann distributionQ8) Derive relation for density of states?A8) A parameter of interest in the study of conductivity of metals and semiconductors is the density of states. The Fermi function F(E) gives only the probability of filling up of electrons in a given energy state. It does not give the information about the number of electrons that can be filled in a given energy state, to know that we should know the number of available energy states called density of states.Density of states is defined the as the number of energy states per unit volume in an energy interval of a metal. It is use to calculate the number of charge carriers per unit volume of any solid.

Figure 2: Positive octant of n space Let us constant a sphere of radius “n” in space with quantum numbers nn, ny and nz

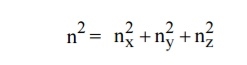http://img.brainkart.com/extra/0aaVI7n.jpg

The sphere is further divided into many shells represents a particular combination of quantum numbers and represents particular energy value.Therefore, the number of energy states within a sphere of radius

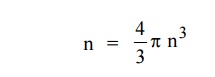http://img.brainkart.com/extra/j9Brfev.jpg

Let us consider two energy values E and E + dE can be found by finding the number of energy states between the shells of radius n and n+ dn from the origin. Since the quantum numbers are positive integers, n values can be defined only in the positive octant of the n – space. The number of available energy states within the sphere of radius “n” due to one octant.

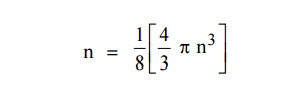http://img.brainkart.com/extra/xRaZqg8.jpg

Similarly the number of available energy states within the sphere of radius n+dn corresponding energy.

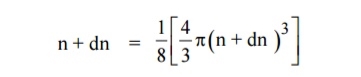http://img.brainkart.com/extra/vV2Z8P2.jpg

The number of available energy states between the shells of radius n and n + dn (or) between the energy levels E and E + dE

The number of available energy states between the energy interval dE

Since the higher powers of dn is very small, dn2 and dn3 terms can be neglected.

We know that the allowed energy values is

Differentiating equation (4) with respect to ‘n’

Each electron energy level can accommodate two electrons as per Pauli’s exclusion principle. (Spin up and Spin down = 2 (e) × density of states).

Q9) Explain Fermi level for Intrinsic semiconductors and what is the effect of temperature on Fermi level?A9) Fermi LevelWe know that in intrinsic semiconductor Electron concentration ‘n’ = Hole concentration ‘p’ Equating Equations (15) and (27), we get

images

Taking logarithms on both sides, we get

……………… (29)Normally, mh* is greater than me*, since ln

is very small so that EF is just lie in the middle of energy gap Temperature effect on Fermi levelFermi level slightly rises with increase of temperature.But in case of pure intrinsic semiconductor like Si and Ge, mh* ≈ me* so in these cases Fermi level lies at the middle of energy gap.Q10) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.A10.

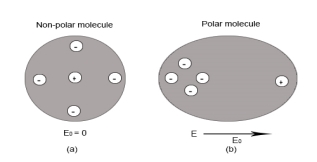
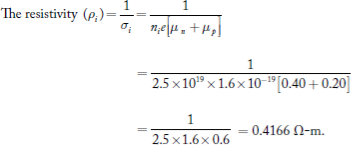Q11) Find the resistivity of an intrinsic semiconductor with intrinsic concentration of 2.5 × 1019 per m3. The mobilities of electrons and holes are 0.40 m2/ V-s and 0.20 m2/ V-s.A11) Given data are:Intrinsic concentration (ni) = 2.5 × 1019/m3Mobility of electrons (μn) = 0.40 m2/V-sThe mobility of holes (μp) = 0.20 m2/V-sThe conductivity of an intrinsic semiconductor (σi) = nie[μn + μp] images

Q12) What are the differences between polar and non-polar molecules? Also discuss the effect of electric field on dielectric? A12) Polar Molecules: Polar Molecules are those in which centre of gravity of positive and negative charge does not coincide with each other. This is because they all are asymmetric in shape. Examples: H2O, CO2, NO2 etc.Non-Polar Molecule: Non-polar molecules are those in which centre of gravity of positive charge and negative charge coincide with each other. The molecule has zero dipole moment as they all are symmetric in shape. Examples: O2, N2, H2 etc.

Response of Dielectric to External Electric FieldIn case of Polar Molecules -When the electric field is not present, it causes the electric dipole moment of these molecules in a random direction. This is why the average dipole moment is zero. If the external electric field is present, the molecules align themselves in the direction electric field and resulted in having dipole moment.In case of Non Polar Molecules – As we know nonpolar molecule has zero dipole moment. In spite of zero dipole, when a dielectric nonpolar material is placed in an electric field. The positive and the negative charges in a nonpolar molecule experience forces in opposite directions. This force causes the separation between the charges and hence nonpolar molecule experiences induced dipole moment.

Figure a (left) Non Polar Molecule Figure b (right) Polar MoleculeQ13) Dipoles are created when dielectric is placed in __________
a) Magnetic Field
b) Electric field
c) Vacuum
d) Inert EnvironmentA13) b
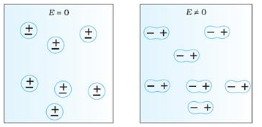
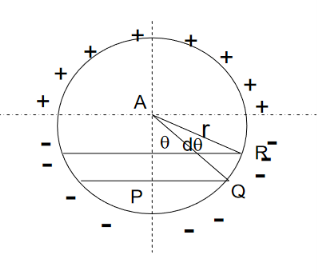
When the dielectric is placed in an electric field, like between the parallel plates of a capacitor, the dipoles are created and they tend to align themselves parallel to the direction of the electric field.Q14) Derive Claussius -Mosotti equation?A14) In dielectric solids, the atoms or molecules experience not only the external applied electric field but also the electric field produced by the dipoles. The resultant electric field acting on the atoms or molecules of dielectric substance is called the local field or an internal field.To find an expression for local electric field on a dielectric molecule or an atom, we consider a dielectric material in the electric field of intensity E, between the capacitor plates so that the material is uniformly polarized, as a result opposite type of charges are induced on the surface of the dielectric near the capacitor plates. The local field is calculated by using the method suggested by Lorentz.According to this method, Internal field or Local field in solidsConsider a dielectric material and is subjected to external field of intensity E1. The charges are induced on the dielectric plate and the induced electric field intensity is taken as E2. Let E3 be the field at the center of the material. E4 be the induced field due to the charges on the spherical cavity. The total internal field of the material is

………..(1)

Now consider the Electric field intensity applied E1

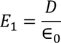………..(2)We know

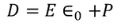………..(3)Substituting the Electric flux density D in E1, we get

………..(4)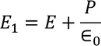

………..(5)E2 is the Electric field intensity due to induced or polarized charges

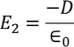………..(6)Here the charge is induced due to the induced field so the electric flux density D changes to the electric polarization P

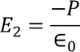………..(7)Since we have considered that the specimen is non-polar dielectric material, at the center of the specimen the dipole moment is zero and hence the electric field intensity at the center is zero due to symmetric structure.

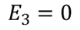………..(8)Now consider a circle from the center of the dielectric material. Calculation of the electric field intensity E4 on the surface of spherical cavity.As we know the polarization P is the induced charge per unit area

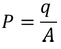………..(9) Here the polarization changes to its component so we will take the component which is contributing.

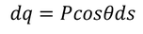………..(10)Now this equation can be solved by finding out the values of the charge dq in the surface are dA. We know the Electric field intensity E

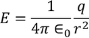………..(11)Multiplying with the cosine angle on both the sides we get

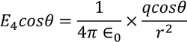………..(12)Now by applying all the present condition for the above equation we

………..(13)Now substituting the charge dq in the above equation we get

………..(14)

If dA is the surface area of the sphere of radius r lying between θand θ+dθis the direction with reference to the direction of the applied force, then dA= 2π(PQ)(QR) but sinθ= PQ/r, PQ = rsinθ ………..(15)and dθ=QR/r, QR=r dθ ………..(16)

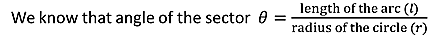Hence dA= 2πrsinθrdθ= 2πr2sinθdθ ………..(17)Now substituting all the values in the electric field intensity on the spherical cavity E4 we get,

………..(18)

Substituting (17) in (18), we get

………..(19)

Integrating with in the limits 0 to π

………..(20)

On solving the integration we get,

………..(21)

So the total electric field

………..(22)

Hence the Internal field obtained is

………..(23)

Claussius -Mosotti EquationIt gives the relation between the dielectric constant and the ionic polarizability of atoms in dielectric material. If there are N number of atoms, the dipole moment per unit volume which is called Polarization is given by,

………..(24)

we know internal field

………..(25)

From above equations

………..(26)

we know polarization from the relation between polarization and dielectric constant

………..(27)

from the above two equations we get,

………..(28)

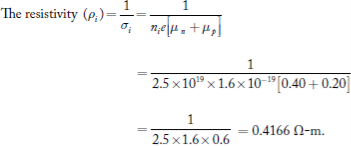Q15) Find the resistivity of an intrinsic semiconductor with intrinsic concentration of 2.5 × 1019 per m3. The mobilities of electrons and holes are 0.40 m2/ V-s and 0.20 m2/ V-s.A15) Given data are:Intrinsic concentration (ni) = 2.5 × 1019/m3Mobility of electrons (μn) = 0.40 m2/V-sThe mobility of holes (μp) = 0.20 m2/V-sThe conductivity of an intrinsic semiconductor (σi) = nie[μn + μp] images

Q16) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.A16)

Q17) For an intrinsic Semiconductor with a band gap of 0.7 eV, determine the position of EF at T = 300 K if m*h = 6m*eA17)

Q18) Discuss application of dielectrics in transformers?A18) We can say that transformer is basic arrangement of conductors and dielectric insulators. Transformer is a static device consisting of two or more windings which comprehend a common magnetic field. We know that transformer contains two parts: Primary coil and secondary coil. Energy transforms from primary coil to secondary coil only through magnetic induction, not by any electrical path. So to avoid electrical conduction we must use dielectric insulator at all possible places.In transformer, the dielectric materials are used as insulator as well as cooling agents. Based on the applications of dielectric in transformer they fall into three groups.1. Gaseous Dielectric in transformer.2. Liquid dielectric in transformer.3. Solid dielectric in transformer.Gaseous Dielectric in Transformer

The usage of nitrogen in transformer prevents oxidation and reduces the rate of deterioration.

Sulphur hexafluoride dielectric is an electronegative gas which is used in transformer.

It is non-toxic, non-inflammable and chemically inert.

Liquid Dielectric in Transformer

Transformer oil - It is a class of mineral insulating oil and is used as a coolant.

It also maintains the insulation of the winding.

Fluorocarbon liquids are used in large transformer to give high heat transfer rates together with high dielectric strength.

Solid Dielectric in Transformer

Fibrous materials are used in air cooled Transformers.

Cotton tape is used for insulating the conductors of oil cooled transformers.

High quality synthetic resin bonded paper in the form of cylinders is used as an insulator between core and coils and also between primary and secondary windings.

Press board or press paper is used as a filling, and as a packing material between coils.

Q19) Discuss success and failures of QFET?A19) Success of QFET1. This theory explains the specific heat capacity of materials.One of the difficulties is to the heat capacity of the conduction electrons. According to classical theory a free particle should have a heat capacity of

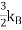where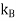

, is the Boltzmann constant. If we have N number of atomsand each give one valence electron to the electron gas, and the electrons are freely mobile, then the electronic contribution to the heat capacity should be

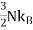, same as for the case of atoms of a monatomic gas. But the observed electronic contribution at room temperature is usually less than this value. How can the electrons participate in electrical conduction processes as if they were mobile, while not contributing to the heat capacity?This important discrepancy is removed with the help of Quantum theory of free electrons. It was discovered that the specific heat vanishes at absolute zero and that at low temperatures it is proportional to the absolute temperature.When we heat the specimen from absolute zero, not every electron gains energy

as expected classically, but only those electrons in orbitals within an energy range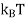

of the Fermi level are excited thermally. This gives an immediate qualitative solution to the problem of the heat capacity of the conduction electron gas. If N is the total number of electrons, only a fraction of the order of T/TF can he excited thermally at temperature T,This is because only these electrons lie within an energy range of the order of

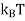of the top of the energy distribution.Each of these NT/TF electrons has a thermal energy of the order of kBT.The total electronic thermal kinetic energy U is of the order ofU

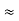(NT/TF)

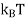The electronic heat capacity is given byC =

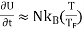and is directly proportional to T, in agreement with the experimental results discussed in the following section. At room temperature C is smaller than the classical value

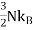, by a factor of the order of 0.01 or less, for TF

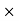104K.2. This theory explains photo electric effect, Compton Effect and block body radiation etc.3. This theory gives the correct mathematical expression for the thermal conductivity of metalsThe temperature-dependent part of the electrical resistivity is proportional to the rate at which an electron collides with thermal phonons and thermal electrons. The collision rate with phonons is proportional to the concentration of thermal phonons. Here the phonon concentration is proportional to the temperature T. So using quantum theory result the thermal conductivity can be calculated.Failures of Quantum free electron theory1. This theory fails to explain bands presence and also not able to distinguish between metal, semiconductor and Insulator2. According to this theory, only two electrons are present in the Fermi level and they are responsible for conduction which is not true.3. Quantum free electron theory not able to explain the positive value of Hall Co-efficient. Q20) Give assumptions of quantum free electron theory?A20) The failure of classical free electron theory paved this way for Quantum free electron theory. It is introduced by Sommerfeld in 1928. Arnold Sommerfeldovercomes many drawbacks of the classical free electron theory by applying quantum mechanical principles in 1928.Quantization of electrical energy levels is added here. He also used the Pauli Exclusion Principle in restricting the energy values of electron. His theory is known as Quantum Free Electron TheoryThe main assumptions of quantum free electron theory are,

In a metal the available free electrons are fully responsible for electrical conduction. The energy levels of the electrons that responsible for the conduction are quantised.

The electrons move in a constant potential inside the metal but they cannot come out from this potential but remain confined within its boundaries.

The distribution of electrons in various allowed energy levels occur according to the Pauli Exclusion Principle.

Electrons have wave nature, the velocity and energy distribution for the electrons given by Fermi-Dirac distribution function.

Both the attraction between the electrons and the lattice ions, and the repulsion between the electrons themselves are ignored.

The energy is loss due to interaction of the free electron with the other free electron.

Q21)Derive relation for conductivity of a semiconductors? A21) In semiconductor, the conduction band electron and valance band hole participate in electrical conduction. To obtain expression for electrical conductivity consider an intrinsic semiconductor bar which is connected to external battery as shown in figureThe electric field exist along x direction. The field accelerate electrons (conduction electrons) along negative X-direction and holes along positive X-direction. They starts moving with a constant velocity called Drift velocity vd The total current in the semiconductor (due to both electron and hole)I = Ie +Ihor total current densityJ = Je +Jh ..........(1)

Figure 11: Conductivity of semiconductorsIn order to find the current density of electrons, let the concentration of electrons are 'n' , charge is 'e' and drift velocity is 've', ThenJe =neve ..........(2)The drift velocity produced per unit electric field is called 'mobility' , Thusμe =

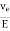orμeE =

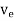substituting in equation 2Je =neμeE ..........(3)From Ohms law, J = E where Je = eEJe =neμeE = eE ..........(4)e = neμe ..........(5)Similarly current density for holesJp =peμpE = pE ..........(6)And conductivityp = peμp ..........(7)Substituting value of Je and Jp from eq 4 and 6 in eq 1, we getJ = neμeE + peμpE J = (neμe + peμp)E ..........(8)From Ohms law J = E = neμe + peμpwheree = neμe andp = peμpAlso ni =CT3/2e -Eg/2kT ..........(9)Therefore  = nie(μe + μp) = CT3/2e -Eg/2kT e(μe + μp) ..........(10)The mobilities of carrier depend upon temperature asμ

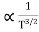For Electrons μe

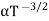and for holes μp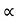

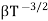μe + μp=

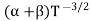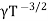..........(11)Using equation 11 in equation 10 = CT3/2e -Eg/2kT e

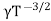 = C e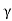

e -Eg/2kTLet B = C e

we get  = Be -Eg/2kT ..........(12) Q22) Derive relation for Fermi energyand show Fermi energy of a metal depends only on the density of electrons of that metal?A22) Let us recall the formula for density of states (we derived density of states under article 5.4, equation 7)

Each electron energy level can accommodate two electrons as per Pauli’s exclusion principle. (Spin up and Spin down = 2 (e) × density of states).

Carrier Concentration In Metals Let N(E) dE represents the number of filled energy states between the interval of energy dE, normally all the energy states will not be filled dN = N (E) dE F(E)

Normally all the states are not filled states, filling of electrons is a given energy state is given by Fermi-function F(E). Let dn represents the number of filled energy states. In this case of material of absolute zero the upper occupied level is EF and for all the levels below EF, F(E)=1 (at T = 0 K the maximum energy level that can be occupied by the electron is called Fermi energy level EF T = 0 K F(E) = 1).Integrating equation (8) within the limits 0 to EF0 us can get the number of energy states of electron (N)

Hence the Fermi energy of a metal depends only on the density of electrons of that metal.

Sign Up