Aryabhatta Knowledge University (AKU)

Civil Engineering

Engineering Mechanics

Solved Exam Paper 2019

Question. State and prove parallelogram law of forces

The law of parallelogram of forces states that if two vectors acting on a particle at the same time be represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point their resultant vector is represented in magnitude and direction by the diagonal of the parallelogram drawn from the same point .

Let us assume that the two vectors A and B, inclined at angle θ, be acting on a particle at the same time. Let they be represented in magnitude and direction by two adjacent sides OP and OS of parallelogram OPQS, drawn from a point O.

According to parallelogram law of vectors, their resultant vector will be represented by the diagonal of the parallelogram.

Magnitude and Direction of Resultant:

Draw a perpendicular QN to OP produced.

And let us assume that OP=A, OS= PQ= B, OQ=R and angle SOP= angle QPN = θ.

Now considering this if we proceed further, in the case of triangle law of vector addition, the magnitude and direction of resultant vector will be given by

R= sqrt of A^2 + B^2 + 2 AB cosθ

Tan B = B sinθ/ A+B cosθ

Special cases:-

(1) When two vectors are acting in the same direction, then θ= 0 , cosθ=1 and sinθ= 0

R= sqrt of A^2 + B^2 + 2 AB

=sqrt of (A+B)^2 = A + B

Tan Beta = B X 0/ A+B = 0

Beta = 0

Thus for two vectors acting in the same direction the magnitude of the resultant vector is equal to the sum of the magnitudes of two vectors and act along the direction of A and B.

(2) When two vectors are acting in opposite directions , then θ= 180 , cos θ= -1 and sinθ= 0

R= sqrt of A^2+ B^2+ 2 AB (-1)

= sqrt of (A-B) or (B-A)

Tan beta = B X 0/ A+ B (-1)= 0

Beta = 0 or 180.

Thus for two vectors acting in opposite directions, the magnitude of the resultant vector is equal to the difference of the magnitudes of the two vectors and acts in the direction of bigger vector.

(3) When two vectors act at right angle to each other θ = 90 , sinθ = 1 and cosθ  = 0

R= sqrt of A^2+B^2 + 2 AB (0)

= sqrt of A^2+B^2

Tan beta = B(1)/A+B(0)= B/A

Or, Beta = tan^-1 B/A

1. It is to be noted that the magnitude of the resultant of two vectors is maximum, when the vectors act in the same direction and is minimum when they act in opposite directions.

2. It should be noted that while finding the resultant vector of two vectors by the parallelogram law of vector addition, the two vector A and B should be either act towards the point or away from the point.

Question. State the Varignon’s principle of moments

Varignon's Theorem, also often called the principle of moments, is a very useful tool in scalar moment calculations. In cases where the perpendicular distance is hard to determine, Varignon's Theorem offers an alternative to finding that distance.

In its basic form, Varignon's states that if we have two or more concurrent forces, the sum of the moments that each force creates about a single point will be equal to the moment created by the sum of those forces about the same point.

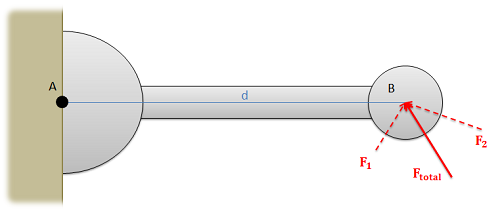If the sum of F1 and F2 is Ftotal, then we can assume that the sum of the moments about point A exerted by F1 and F2 will be equal to the moment exerted about point A by Ftotal

On its surface this doesn't seem that useful, but in practice we will often use this Theorem in reverse by breaking down a force into components (the components being a set of concurrent forces). We can solve for the moment exerted by each component (where perpendicular distance d is easier to find) and then simply add together the moments from each component to find the moment from the original force.

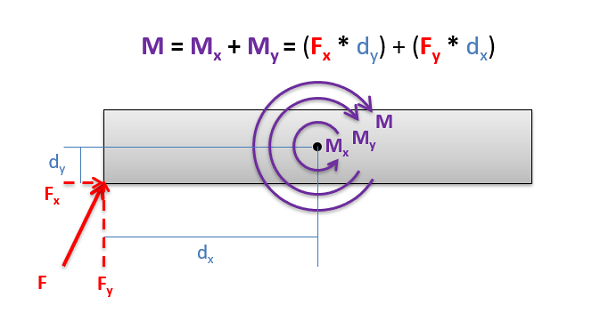Breaking a force into components to solve for the overall moment

When finding the moment of Force F about the center point, it will be easier to break down the force into components and find the moments of each component rather than trying to find the perpendicular distance directly using complex geometric relationships.

Question. Prove the parallel axis theorem in determination of moment of inertia of areas with the help of neat sketch

Parallel axis theorem states that

The moment of inertia of a body about an axis parallel to the body passing through its center is equal to the sum of moment of inertia of body about the axis passing through the center and product of mass of the body times the square of distance between the two axes.

Parallel Axis Theorem Formula

Parallel axis theorem statement can be expressed as follows:

I = Ic + Mh2

Where,

I is the moment of inertia of the body

Ic is the moment of inertia about the center

M is the mass of the body

h2 is the square of the distance between the two axes

Let Ic be the moment of inertia of an axis which is passing through the center of mass (AB from the figure) and I be the moment of inertia about the axis A’B’ at a distance of h.

Consider a particle of mass m at a distance r from the center of gravity of the body.

Then,

Distance from A’B’ = r + h

I = ∑m (r + h)2

I = ∑m (r2 + h2 + 2rh)

I = ∑mr2 + ∑mh2 + ∑2rh

I = Ic + h2∑m + 2h∑mr

I = Ic + Mh2 + 0

I = Ic + Mh2

Hence, the above is the formula of parallel axis theorem.

Parallel Axis Theorem of Rod

The parallel axis theorem of rod can be determined by finding the moment of inertia of rod.

Moment of inertia of rod is given as:

I = 13 ML2

The distance between the end of the rod and its center is given as:

h = L2

Therefore, the parallel axis theorem of rod is:

Ic = 13ML2 – ML22

Ic = 13ML2 – 14ML2

Ic = 112 ML2

Question. How will you distinguish between static friction and dynamic friction?

Question. Define perfect, Deficient and redundant trusses

Perfect Truss

A Truss said to be Perfect Truss if it fulfill the below condition

m=2j-3

Where

m= number of members

j= number of joints

Perfect Truss does not collapse under loading.

Imperfect or Deficient Truss

If a given member in the structure is less than the required member than it is called imperfect or deficient truss.

The condition of Deficient Truss is

m<2j-3

Where

m= number of members

j= number of joints

Deficient Truss collapse when we apply load on it.

Redundant Truss

A Truss is said to be Redundant if has more member than required.

The equation for Redundant Truss are as follows

m>2j-3

Where

m= number of members

J= number of joints

Redundant Truss does not collapse when we apply load on it

Question. What do you understand by the term “energy”? Explain various form of mechanical energies

Basically, energy is the ability to do work. While it could not be created nor destroyed, energy could be transferred or change. By being transferred to an object, it is able to do work on such object. In order to stay alive, living things such as humans require available. For humans, various forms of energy are needed from food to energy resources such as fossil fuels. Humans, and other organisms, also need energy in order to move and change in position. This where mechanical energy comes in.

Mechanical energy is a form of energy possessed by an object due to its position or motion. Objects have mechanical energy whether they move or stay in position relative to a zero potential energy position. This means that any object that possesses mechanical energy – whether through movement or due to its position – could do work. Work is described here as the movement of an object when a force is applied to it.

The mechanical energy of an isolated system – whether a physical system or a thermodynamic system – remains constant in time as long as the system is devoid of non-conservative forces such as friction. Though mechanical energy could not be created nor destroyed in an isolated system, it could be converted into other forms of energy.

The form of mechanical energy that is possessed by objects which are in motion is called kinetic energy. An object that is in motion – whether it is horizontal or vertical motion – possesses kinetic energy. Its name was derived from the Greek word “kinesis” which means “motion.”

Kinetic energy may come in various forms. The first form is rotational kinetic energy, the energy that is produced due to rotational motion. The second form is vibrational kinetic energy which is generated due to the movement of vibrations. The third is translational kinetic energy, the energy produced due to the motion from one location to another.

The type of mechanical energy that is possessed by objects at rest, or due to their position, is called potential energy. It could also be the stored energy which an object has. It was introduced by William Rankine, a 19th-century engineer, and physicist.

Potential energy comes in three forms – gravitational potential energy, electric potential energy, and elastic potential energy.

Gravitational potential energy refers to the energy that is stored in objects due to their vertical position. Such energy is stored due to the gravitational pull of the Earth for the objects.

Electric potential energy could be attained when different or alike charges repel or attract each other. The charges could either be positive or negative. Opposite charges attract each other while similar charges repel each other.

Elastic potential energy, on the other hand, refers to the energy that is stored in elastic materials due to stretching and compression. The amount of stored elastic potential energy could be correlated to the amount of stretch of the device.

Both kinetic and potential energy are essential components of the universe. They affect the movement and position of particles within the space-time fabric. Kinetic energy, in particular, is significant because it affects the movement of matter, down to the atomic level. On the other hand, potential energy could help determine the form of existence of matter at the atomic level.

Question. What is simple pendulum? Under what conditions its motion is regarded as simple harmonic?

A point mass attached to a light inextensible string and suspended from fixed support is called a simple pendulum. The vertical line passing through the fixed support is the mean position of a simple pendulum.

The vertical distance between the point of suspension and the centre of mass of the suspended body (when it is in mean position) is called the length of the simple pendulum denoted by L.

A simple pendulum is a mechanical arrangement that demonstrates periodic motion. The simple pendulum consists of a small bob of mass ‘m’ suspended by a thin string secured to a platform at its upper end of length L.

Many physical systems exhibit simple harmonic motion (assuming no energy loss): an oscillating pendulum, the electrons in a wire carrying alternating current, the vibrating particles of the medium in a sound wave, and other assemblages involving relatively small oscillations about a position of stable equilibrium.

The motion is called harmonic because musical instruments make such vibrations that in turn cause corresponding sound waves in air. Musical sounds are actually a combination of many simple harmonic waves corresponding to the many ways in which the vibrating parts of a musical instrument oscillate in sets of superimposed simple harmonic motions, the frequencies of which are multiples of a lowest fundamental frequency.

A specific example of a simple harmonic oscillator is the vibration of a mass attached to a vertical spring, the other end of which is fixed in a ceiling. At the maximum displacement −x, the spring is under its greatest tension, which forces the mass upward. At the maximum displacement +x, the spring reaches its greatest compression, which forces the mass back downward again. At either position of maximum displacement, the force is greatest and is directed toward the equilibrium position, the velocity (v) of the mass is zero, its acceleration is at a maximum, and the mass changes direction. At the equilibrium position, the velocity is at its maximum and the acceleration (a) has fallen to zero. Simple harmonic motion is characterized by this changing acceleration that always is directed toward the equilibrium position and is proportional to the displacement from the equilibrium position. Furthermore, the interval of time for each complete vibration is constant and does not depend on the size of the maximum displacement. In some form, therefore, simple harmonic motion is at the heart of timekeeping.

To express how the displacement of the mass changes with time, one can use Newton’s second law, F = ma, and set ma = −kx. The acceleration a is the second derivative of x with respect to time t, and one can solve the resulting differential equation with x = A cos ωt, where A is the maximum displacement and ω is the angular frequency in radians per second. The time it takes the mass to move from A to −A and back again is the time it takes for ωt to advance by 2π. Therefore, the period T it takes for the mass to move from A to −A and back again is ωT = 2π, or T = 2π/ω. The frequency of the vibration in cycles per second is 1/T or ω/2π.