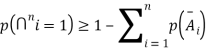Q2. A) Solve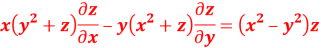     

Answer: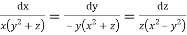

Choose the multipliers as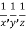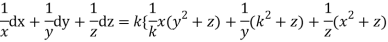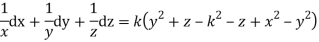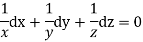

On integration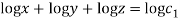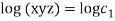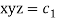

Now again choose the multipliers as x,y,-1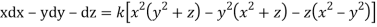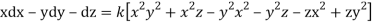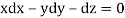

On integration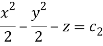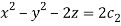

Now on combining both eq. We get a general solution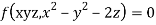

1. Q3. State and prove Rodrigues formula .

Sol- we derive a formula for the legendre polynomials

Formula

Now proof

Let

We shall first establish that the nth derivation of u, that is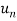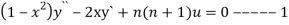

Differ w.r. To x

Or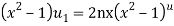

i.e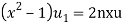

Diff. w.r. To x again, we have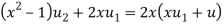

Now differ. The result in timer by applying lebuitz theorem for nth derivation of a product given by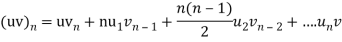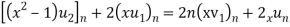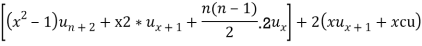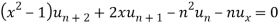

Or

This can be put in the form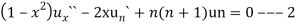

Comparing 2 with 1 we conclude that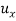

Also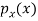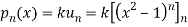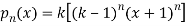

Applying Leibnitz theorem for the RHS we have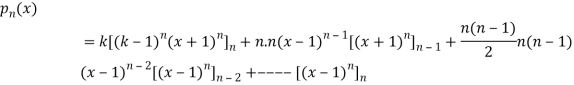

It should be observed that if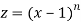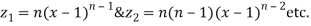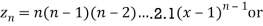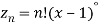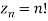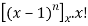

Putting x =1 in eq. 1 all the terms in RHS become zero except the last term which becomes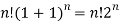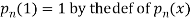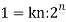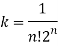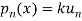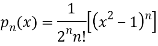

Q4. A coin is tossed. If it turns up H, two balls will be drawn from urn A otherwise 2 balls will be drawn from urn B. Urn A contains 3 red and 5 blue balls , urn B contains 7 red and 5 blue balls. What is the probability that urn A is used , given that both balls and blue? (find in both cases, when balls were chosen with replacement and without replacement).   

   Sol- let us define the following events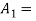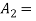

E= two blue balls are drawn (with reputation)

Then we have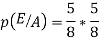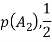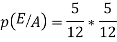

So,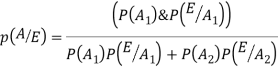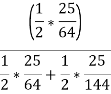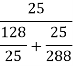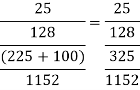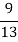

(b) for event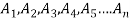

Prove that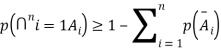

Q5. State and prove bayes theorem.

Sol. –it states that “If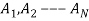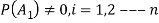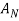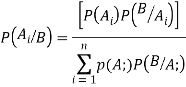

Proof- by compound theorem of probability ,

We get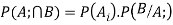

Or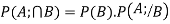

Given that , B is any other event which occur with A or A; or …..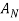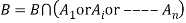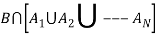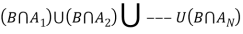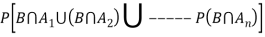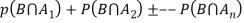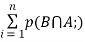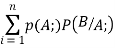

Again from II

                                          7

(b) a random variable X follows binominal distribution with parameter n=40 and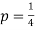

a.

b.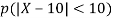