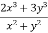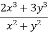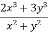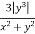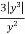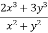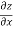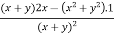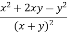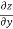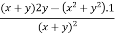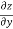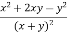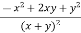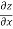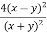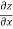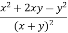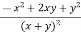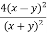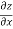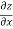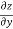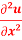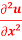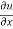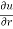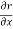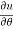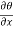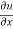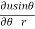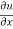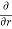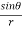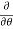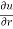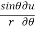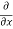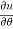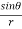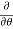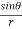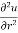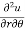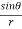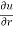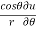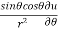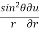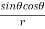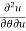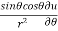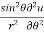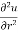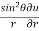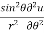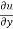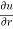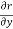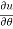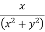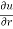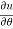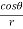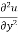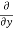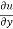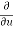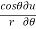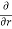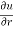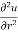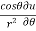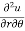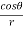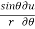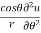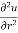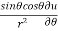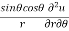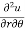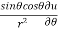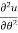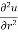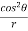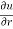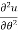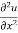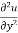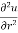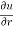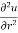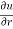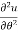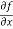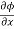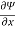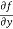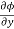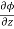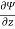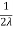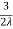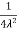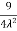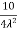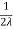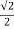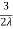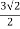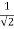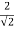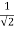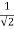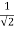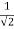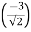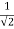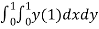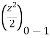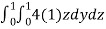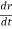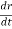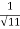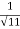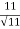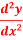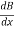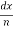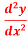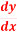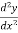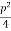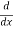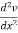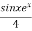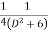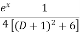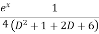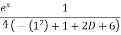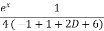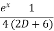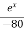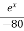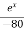Q 1 a) If y=A cos (log x) + B sin (log x), Show that x2yn+2 +(2n+1) * yn+1 + (n2 + 1) yn=0 where yn= dny/dxn

  If y = Acos(logx) +  Bsin(logx)  ------------(1)

 Differentiating (1) w.r.t x, we get

 y1  = -asin(logx)1/x + bcos(logx)1/x

 xy1   = -asin(logx) + bcos(logx)  ------------(2)

 Diff 2   again w.r.t x, then we get

 xy2  + y1    = -acos(logx)1/x - bsin(logx)1/x

 x2y2  + xy1  =  -[acos(logx) + bsin(logx)]

 x2y2  + xy1   = -y

 y2x2 + y1x + y = 0  ----------------------------(3)

 Diff  3  by Leibnitzle theorem n times, we get

 [ yn+2x2 + nc1 yn+12x + nc2 yn.2 ]  +  [ yn+1x + nc1 yn-1]  +  yn   =  0

 x2yn+2 + 2nxyn+1  + xyn+1  +n(n-1)yn + nyn + yn = 0

 x2yn+2 + (2n+1)xyn+1 + (n2+1)yn = 0

Q2 a)   Show that the following function is continuous at the point (0,0):

f(x,y)             ,   (x,y)  != (0,0)

    0  ,    (x,y)  = (0,0)

      Answer:           

f(x,y)             ,   (x,y)  != (0,0)

    0  ,    (x,y)  = (0,0)

0  < =      |       |    < =     +            =  0 

0  < =                 +            =    2 | x |  + 3 | y |

lt(x,y)-->(0,0)   2 | x |  + 3 | y |   =  0

∴   by the squeez theorem,, we conclude that

lt(x,y)-->(0,0)  f(x,y) = (0,0)  that is =>  lt(x,y)-->(0,0)  = 0

∴ f is continous at (0,0)

Q2 b)   If z(x+y) = x2 + y2   show that

 (- )2  =  4(1--)

solution:

z(x+y) = x2 + y2

z    =  

=     = 

=       =   

(- )  =             =      =   

(- )2  =                          -----------------------------------------------------------1

4(1--) =   4 [ 1 -   -  ]                   

                =              ---------------------------------------------------2

From 1 & 2

(- )2 = 4(1--)

Q3 a)Transform the equation

    +   = 0   into polar coordinates.

Solution:

we have x = rcosθ  , y = rsinθ 

r2 = x2 + y2  ,  θ  =  tan-1y/x

= . + . => (cos θ ) -

=  ()

   = (  cosθ -  .) ( cosθ - )

  =   cosθ(  cosθ- ())  -  .(  cosθ- )

  =   cosθ(  cosθ+ - .) - ( - sinθ+

     cosθ-- )

  = cos2 θ+ - +-      

    + +

  = cos2 θ+ 2- 2 + +

                ----------------------------------------------------------------(1)

  = = + 

  = y/r +     

  = sinθ +

  == ()

  =   (sinθ  + )( sinθ+)

 =    sinθ(sinθ + ) + (  sinθ+ )

 =     sinθ[ sinθ- + + ]  +  [ cosθ [+

   sinθ- + ]

=     sin2θ- + + () +

() - + ()

=     sin2θ- 2+2+  () +

    ()                                    -----------------------------------------------------------(2)

By adding 1 & 2

+ = (sin2θ+cos2θ)+(sin2θ+cos2θ)1/r+ (sin2θ+cos2θ)1/r2

=  (+ 1/r+1/r2)            ans

Q4 Find the extreme values of f( x,y ,z) = 2x+3y+z, such that x2+y2=5 and x+z=1

 f(x,y,z) = 2x + 3y + z            ----------------------(1)

 f(x,y)   = (x2 + y2)  - 5          -----------------(2)

 y(x,z)  = x+z-1                     ------------------(3)

 Lagranges Multipliers Equations are

 + λ + m = 0

 + λ + m = 0

 + λ + m = 0

 2 + λ(2x) + m(1)   = 0          ------------(4)

 3 + λ(2y) + m(0)   = 0          ------------(5)

 1 + λ(0) + m(1)   = 0          ------------(6)      => m = -1

 putting the values of m in (4) and (5), we get

 2 + 2λx – 1 = 0  => 2λx = -1 ,  x = -

 3 + 2λy       = 0  => 2λy  = -3 ,  y = -

  putting the values of x,y in  x2 + y2  = 5 , we get

 + = 5   => = 5

 2λ2 = 1   => λ = +-

 we know that ,  x = - = +- = +-

            y =  - = +-+-

 From (3) , x+z =1 or z = 1-x

 z = 1+-

  putting  x = ,  y = and z = 1 - in equation (1), we get

 f = + + 1 - = + 1 = 5Ö2 + 1

  putting  x = -,  y = -and z = 1 + in equation (1), we get

 f = 2+ 3 + ( 1 + ) = - - +1 +

 f = 1 – 6 Ö2           ans

Q5 Evaluate òòs F.n.ds where F = 4xz i^ + y2ĵ + yzk^ and S is surface of the cube bounded by x=0, y=1, z=0 , z=1, by using Gauss divergence theorem

òòs F¯ n^ ds = òòOABC  F¯ n^ ds +  òòDEFG  F¯ n^ ds +  òòOAFG  F¯ n^ ds +  òòBCDE  F¯ n^ ds +  òòABEF  F¯ n^ ds +

 òòOCDG  F¯ n^ ds                                              -----------------------------------(1)

òòOABC  F¯ n^ ds  =  òòOABC (4xz i^ + y2ĵ + yzk^)(-k)dxdy

   = (as  z = 0)

 òòDEFG (4xz i^ + y2ĵ + yzk^)(k)dxdy  =  òòDEFG yzdxdy

= = [x]0-1 = 1/2

  òòOAFG (4xz i^ + y2ĵ + yzk^)(-j^)dxdz =  òòOAFG y2dxdz  = 6   (as y =0 )

 òòBCDE(4xz i^ + y2ĵ + yzk^)(j^)dxdz     =  òòBCDE (-y2)dxdz

-= (x)0-1(z)0-1 = -1     ( as y = 1)

òòABEF  (4xz i^ + y2ĵ + yzk^).i^ dydz = òò4xzdydz

 ==> 4(y)0-1   =  4 (1) = 2

òòOCDG(4xz i^ + y2ĵ + yzk^)(-i^) dydz = = 0         ( as x = 0 )

on putting these values in (1), we get

òòs F¯ n^ ds = 0 + 1/2 + 6 -1 + 2 + 0  => 3/2

Q 6  (a)    Evaluate {A*{ B * C }}

              i^          ĵ           k^

(B*C)  =     cosq     -sinq     -3

                       2             3        -1

= i^ (sinq + 9) – ĵ (-cosq + 6) + k^ (3cosq + 2sinq)

        i^           ĵ            k^

A*( B * C ) =   sinq  cosq       Q

       (sinq + 9)         (cosq - 6)          (3cosq + 2sinq)

= i^[cosq(3cosq + 2sinq)  -  q(cosq – 6)]

- ĵ[sinq(3cosq + 2sinq) - q(sinq + 9)]

+ k^[sinq(cosq – 6) - cosq (sinq + 9)]

at q = 0

=>  i^[cos0(3cos0 + 2sin0)  -  0(cos0 – 6)]

- ĵ[sin0(3cos0 + 2sin0) - 0(sin0 + 9)]

- ĵ[sin0(3cos0 + 2sin0) - 0(sin0 + 9)]

=> 3i^ - 9k^      ans

Q 6 A particle moves along the curve x=t3 + 1, y=t2, z= 2t+5 where t is the time. Find the components of the velocity and acceleration at t=1 in the direction i+j+3k

 x = t3 + 1 , y = t3 , z = 2t + 5

 ¯r  =  xi^ + yĵ + zk^

       ¯r  =  (t3 + 1)i^ +  (t3)ĵ + (2t + 5)k^

velocity = = 3t2 i^ + 2tĵ + 2k^

when t = 1, we have , = 3 i^ + 2ĵ + 2k^

unit velocity along ( i^ + ĵ + 3k^) =  ( i^ + ĵ + 3k^) / Ö (1 + 1 + 9)

   = ( i^ + ĵ + 3k^)

component of velocity (3 i^ + 2ĵ + 2k^) along ( i^ + ĵ + 3k^)

  = (3 i^ + 2ĵ + 2k^) .  ( i^ + ĵ + 3k^)

  =  (3+2+6) = = Ö11  ans

Q7 (a) Solve by the method of variation of parameters

 + n2y = sec nx

solution: -  (D2 + n2)y = sec nx

        m2 + n2 = 0  => m = +- ni

  cf = c1cosnx + c2sinnx

  y = A'cosnx + B'sinnx          -----------------(I)

  by diff. Equation (1)

 (-nA'sinnx  + B'ncosnx  = secnx)  -------------(II)

 Now multiplying by nsinx in equation (I) & multiplying by cosx in equation (II)

 nsinnx(A'cosnx + B'sinnx = 0)

 cosnx(-nA'sinnx  + B'ncosnx  = secnx)

  A' nsinnx cosnx + B' nsin2 nx  = 0

 - A' nsinnx cosnx + B' ncos2 nx  = 1

-----------------------------------------------------

        nB' (sin2nx + cos2nx) = 1

B' =

=

dB =

A'cosnx + B'sinnx   = 0

A'cosnx + sinnx    = 0

A' = - = - tan nx

òdA = -ò tan nx dx + C2

A = -log sec nx + C2

y = [-log sec nx + C2 ] cos nx + ( + C1)sin nx

Q 7 (b) solve - 2 tanx + 5y = sec x. ex

- 2 tanx + 5y = sin x. ex

y'' – 2 tan xy' + 5y =  sin x. ex

compare with y'' + 8y' + qy = R

p = -2tanx , q = 6, R = sin x. ex

for C.F            µ = e-1/2òpdx

   q1 = q - -

   R1 =

µ = e-1/2ò-2tanx dx = elog secx = sec x

q1 = 5 -(-2tanx)-

    = 5 + sec2x – tan2x = 6

R1 = 

+ q1v = R1

(D2 + 6)v  =

A.E = m2 + 6 =0 => m2 = -6 => m = +- 6i

CF = (C1cos6x + C2sin6x)

P.I = => (sin x. ex)

 = sin x

 = sin x  =>  sin x

 = sin x  => sin x

 = sin x => sin x

 = (D-3)sin x => (Dsin x – 3 sin x)

 = (cos x – 3 sin x)

C.S =  (C1 cos 6x + C2 sin6x) -(cos x – 3 sin x