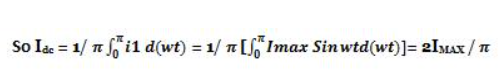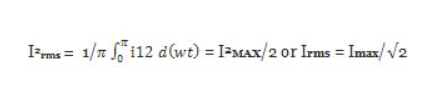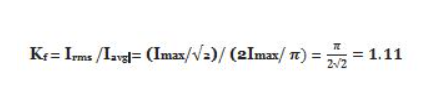![I = I_0 [e^{\dfrac{V}{\eta V_T}}-1]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642968002_935989.png) ………..(1)Figure 1 gives the typical volt-ampere characteristic for a PN diode plotting above equation. With forward bias, the forward current remains essentially zero until the so called Cutin voltage VV of t diode is reached. This cutin voltage is defined as the voltage below which the forward current is less than 1% of the maximum rated current of the diode. This cutin voltage is also known as the turn-on voltage or threshold voltage. The cutin voltage varies with the semiconductor material and with the method of fabrication. Typically, the cutin voltage is about 0.2 volt for Ge diode and about 0.6 volt for Si diode. This higher value of cutin voltage in Si diode results mainly due to low value of IO.From figure 1 we observe that beyond the cutin voltage, the forward current increases rapidly with the increase of forward voltage. In the range of forward voltage, the applied voltage is much larger than VT (0.026 volt at 300 K) so that in above equation we may neglect 1 in comparison with
………..(1)Figure 1 gives the typical volt-ampere characteristic for a PN diode plotting above equation. With forward bias, the forward current remains essentially zero until the so called Cutin voltage VV of t diode is reached. This cutin voltage is defined as the voltage below which the forward current is less than 1% of the maximum rated current of the diode. This cutin voltage is also known as the turn-on voltage or threshold voltage. The cutin voltage varies with the semiconductor material and with the method of fabrication. Typically, the cutin voltage is about 0.2 volt for Ge diode and about 0.6 volt for Si diode. This higher value of cutin voltage in Si diode results mainly due to low value of IO.From figure 1 we observe that beyond the cutin voltage, the forward current increases rapidly with the increase of forward voltage. In the range of forward voltage, the applied voltage is much larger than VT (0.026 volt at 300 K) so that in above equation we may neglect 1 in comparison with 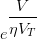 and reduced to the following simpler form
and reduced to the following simpler form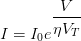 ………(2)With small reverse bias, the reverse current increases with increases with increase in the magnitude of reverse bias. When the reverse bias magnitude exceeds several times VT, we may neglect
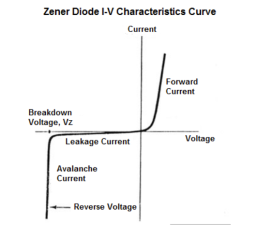
………(2)With small reverse bias, the reverse current increases with increases with increase in the magnitude of reverse bias. When the reverse bias magnitude exceeds several times VT, we may neglect 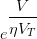 is comparison with I and the reverse current becomes steady at value IO. with further increase of reverse voltage, the breakdown takes place and the reverse current then increases abruptly at an almost constant value of reverse voltage VZ.
is comparison with I and the reverse current becomes steady at value IO. with further increase of reverse voltage, the breakdown takes place and the reverse current then increases abruptly at an almost constant value of reverse voltage VZ.
|
|
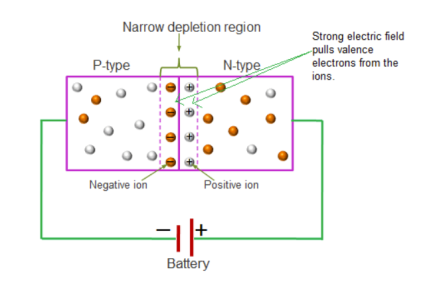
● Zener breakdown occurs at low reverse voltage whereas avalanche breakdown occurs at high reverse voltage.
● Zener breakdown occurs in Zener diodes because they have very thin depletion region.
● Breakdown region is the normal operating region for a Zener diode.
● Zener breakdown occurs in Zener diodes with Zener voltage (Vz) less than 6V.
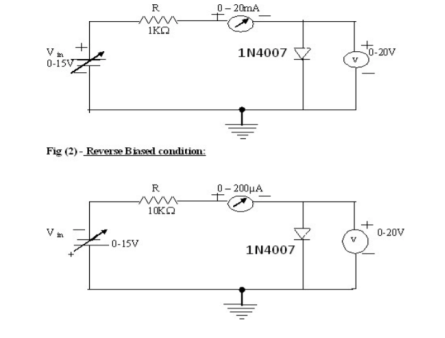
VI characteristics of Zener diodeThe VI characteristics of a Zener diode are shown in the below figure. When a forward biased voltage is applied to the Zener diode, it works like a normal diode. However, when a reverse biased voltage is applied to the Zener diode, it works in a different manner.The VI characteristics of a Zener diode are shown in the below figure.
|
 Where A is nearly constant independent of temperature and dependent on diffusion coefficients of electrons and holes. Eg is the band gap of the semiconductor, kB is the Boltzmann constant. ν is a constant; 1 for germanium and 2 for silicon; and T is the absolute temperature. Band gap of silicon is 1.12eV and that of germanium 0.66eVA-B curve: This curve shows the characteristics of diode for different temperatures in the forward bias. As we can see from the figure given above, that curve moves towards left as we increase the temperature. We know with increase in temperature, conductivity of semiconductors increase. When temperature is high, the electrons of the outermost shell take the thermal energy and become free. So conductivity increases with temperature. Hence with increase in temperature, the A-B curve would shift towards left i.e. curve would rise sharply and the breakdown voltage would also decrease with increase in temperature.A-C curve: This curve shows the characteristics of diode in the reverse biased region till the breakdown voltage for different temperatures. We know ni concentration would increase with increase in temperature and hence minority charges would increase with increase in temperature. The minority charge carriers are also known as thermally generated carriers and the reverse current depends on minority carriers only. Hence as the number of minority charge carriers increase, the reverse current would also increase with temperature as shown in the figure given on the previous page. The reverse saturation current gets double with every 10 C increase in temperature.C-D curve: This curve shows the characteristics of a diode in reverse biased region from the breakdown voltage point onwards. As with increase in temperature, loosely bonded electrons are already free and to free the other electrons, it would take more voltage than earlier. Hence breakdown voltage increases with increase in temperature as depicted in the figure shown in the figure given on the previous page..B) Sketch the circuit of a voltage multiplier and explain its operation.
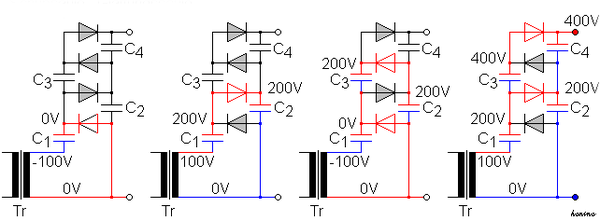
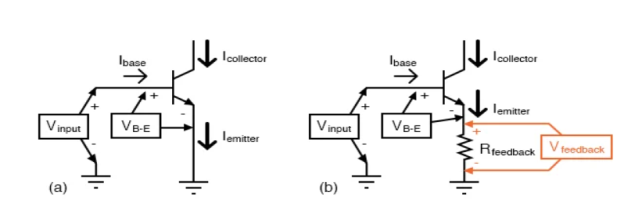
Where A is nearly constant independent of temperature and dependent on diffusion coefficients of electrons and holes. Eg is the band gap of the semiconductor, kB is the Boltzmann constant. ν is a constant; 1 for germanium and 2 for silicon; and T is the absolute temperature. Band gap of silicon is 1.12eV and that of germanium 0.66eVA-B curve: This curve shows the characteristics of diode for different temperatures in the forward bias. As we can see from the figure given above, that curve moves towards left as we increase the temperature. We know with increase in temperature, conductivity of semiconductors increase. When temperature is high, the electrons of the outermost shell take the thermal energy and become free. So conductivity increases with temperature. Hence with increase in temperature, the A-B curve would shift towards left i.e. curve would rise sharply and the breakdown voltage would also decrease with increase in temperature.A-C curve: This curve shows the characteristics of diode in the reverse biased region till the breakdown voltage for different temperatures. We know ni concentration would increase with increase in temperature and hence minority charges would increase with increase in temperature. The minority charge carriers are also known as thermally generated carriers and the reverse current depends on minority carriers only. Hence as the number of minority charge carriers increase, the reverse current would also increase with temperature as shown in the figure given on the previous page. The reverse saturation current gets double with every 10 C increase in temperature.C-D curve: This curve shows the characteristics of a diode in reverse biased region from the breakdown voltage point onwards. As with increase in temperature, loosely bonded electrons are already free and to free the other electrons, it would take more voltage than earlier. Hence breakdown voltage increases with increase in temperature as depicted in the figure shown in the figure given on the previous page..B) Sketch the circuit of a voltage multiplier and explain its operation.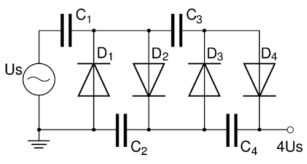 A voltage multiplier is an electrical circuit that converts AC electrical power from a lower voltage to a higher DC voltage, typically using a network of capacitors and diodes.Voltage multipliers can be used to generate a few volts for electronic appliances, to millions of volts for purposes such as high-energy physics experiments and lightning safety testing. Assuming that the peak voltage of the AC source is +Us, and that the C values are sufficiently high to allow, when charged, that a current flows with no significant change in voltage, then the (simplified) working of the cascade is as follows:Illustration of the described operation, with +Us = 100 V
A voltage multiplier is an electrical circuit that converts AC electrical power from a lower voltage to a higher DC voltage, typically using a network of capacitors and diodes.Voltage multipliers can be used to generate a few volts for electronic appliances, to millions of volts for purposes such as high-energy physics experiments and lightning safety testing. Assuming that the peak voltage of the AC source is +Us, and that the C values are sufficiently high to allow, when charged, that a current flows with no significant change in voltage, then the (simplified) working of the cascade is as follows:Illustration of the described operation, with +Us = 100 V
|
3. DC Output Voltage Average or dc value of voltage across the load is given as
4. Root Mean Square (RMS) Value of Output Voltage
5. Rectification Efficiency Power delivered to load,
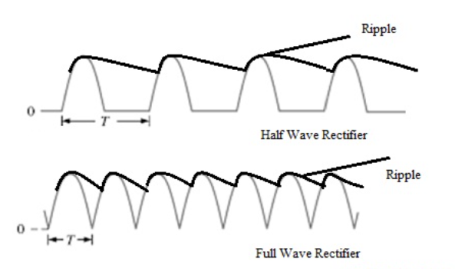
7. Ripple Factor Form factor of the rectified output voltage of a full wave rectifier is given as
So, ripple factor, γ = (1.11 * 1.11 – 1) = 0.482 8. Regulation The dc output voltage is given as
|
|
|
|
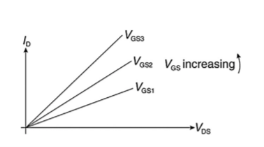
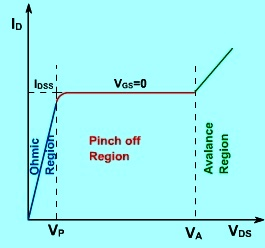
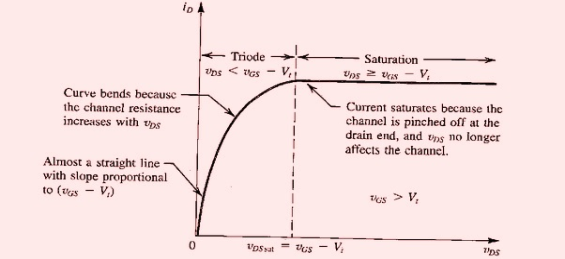
 a mobile gate charge exists only if the gate-source voltage exceeds the threshold voltage. The gate charge Qc(x) is the charge density (Coulombs/m2 ) at position x along the gate. The drain current is equal to:
a mobile gate charge exists only if the gate-source voltage exceeds the threshold voltage. The gate charge Qc(x) is the charge density (Coulombs/m2 ) at position x along the gate. The drain current is equal to: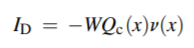 Where W is the width of the MOS device into the paper and v(x) is the “drift velocity” of the charges across the channel. If we assume a low electric field (and hence a long length device), the drift velocity is linearly related to the electric field with particle mobility as a proportionality constant, as:
Where W is the width of the MOS device into the paper and v(x) is the “drift velocity” of the charges across the channel. If we assume a low electric field (and hence a long length device), the drift velocity is linearly related to the electric field with particle mobility as a proportionality constant, as:
|
|
|
|
|