| solved university exam paper 2019 for electrical and electronic material

EEM

Aryabhatta Knowledge University (AKU)Electronics and Communications EngineeringElectrical and Electronic MaterialSolved Exam Paper 2019Question. Identify the miller indices of the close packed planes in an FCC crystal.Answer: Face Centered Cubic Structure consists of an atom at each cube corner and an atom in the center of each cube face. A hard sphere concept can be used to describe atomic packing in unit cells. The FCC structure is shown in fig.la. The distance along unit cell edges is called the lattice parameter, OQ.For cubic crystals the lattice parameter is identical in all three crystal axes. If a corner atom of the FCC unit cell is removed, six atoms are revealed in a hexagonal array. These atoms are closed packed, i.e. they cannot be packed any tighter, and each atom touches its neighbor in any direction. Since a close packed plane such as this can be achieved by removing each of the eight corner atoms and because eight such planes form an octahedron, they are called the 'Octahedral' planes. Thus the FCC structure has four sets of two parallel planes. As parallel planes with the same atomic arrangement are equivalent the FCC structure has four equivalent close packed planes. Using Miller indices from the previous crystallography experiment show them to be {111} planes. Thus the FCC structure has four {111} close packed planes. The atomic arrangement is shown in fig.. Three close packed directions are shown as well. These correspond to (110) directions diagonally across cube faces. There are three of these for each {111} plane. Therefore, FCC structures have twelve possible combinations of {111} and (110).

An FCC structure has close packed octahedral planes, but these are tilted relative to the crystal axes. The FCC structure is made up of layers of octahedral,-type planes. These stack in a sequence ABC ABC as shown in fig.. A, B and C are atom center sites relative to a close packed layer. If atoms in the first-close packed layer sit in position A they form the arrangement shown in fig. The next row of atoms will sit in troughs between the hard sphere atoms, positions B or C. However both positions cannot be occupied. For FCC structures, the second layer of atoms chooses site B. Troughs left after the second layer are A or C, see fig. Choice of C produces a stacking sequence of ABC, the FCC structure. The atom in the center of a close packed plane, such as fig.3a, has six nearest neighbors in the octahedral plane above (ie B positions), and 3 below, (ie C positions). Therefore the coordination number of FCC structures is 6 + 3 + 3 = 12.

Question. Face-centered tetragonal geometry does not exist. DiscussAnswer: In crystallography, the tetragonal crystal system is one of the 7 lattice point groups. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (a by a) and height (C, which is different from a). There are two tetragonal crystal structure types. Bravais lattices: the simple tetragonal (from stretching the simple-cubic lattice) and the centered tetragonal (from stretching either the face-centered or the body-centered cubic lattice). One might suppose stretching face-centered cubic would result in face-centered tetragonal, but face-centered tetragonal is equivalent to body centered tetragonal, BCT (with a smaller lattice spacing). BCT is considered more fundamental, so that is the standard terminology.

Question. Discuss different factors affecting polarizationAnswer: Small cation: the high polarizing power stems from the greater concentration of positive charge on a small area. This explains why LiBr is more covalent than KBr (Li+ 90 pm cf. K+ 152 pm).Large anion: the high polarizability stems from the larger size where the outer electrons are more loosely held and can be more easily distorted by the cation. This explains why for the common halides, iodides, are the most covalent in nature (I- 206 pm).Large charges: as the charge on an ion increases, the electrostatic attractions of the cation for the outer electrons of the anion increases, resulting in the degree of covalent bond formation increasing.Large cations are to be found on the bottom left of the periodic table and small anions on the top right. The greater the positive charge, the smaller the cation becomes and the ionic potential is a measure of the charge to radius ratio.Electronic configuration of the cation: for two cations of the same size and charge, the one with a pseudo noble-gas configuration (with 18 electrons in the outer-most shell) will be more polarizing than that with a noble gas configuration (with 8 electrons in the outermost shell). Thus zinc (II) chloride ( Zn(II) 1s2 2s2 2p6 3s2 3p6 3d10 and Cl- 1s2 2s2 2p6 3s2 3p6 ) is more covalent than magnesium chloride ( Mg(II) 1s2 2s2 2p6) despite the Zn2+ ion (74 pm) and Mg2+ ion (72 pm) having similar sizes and charges.From an MO perspective, the orbital overlap disperses the charge on each ion and so weakens the electrovalent forces throughout the solid, this can be used to explain the trend seen for the melting points of lithium halides.LiF = 870 °C, LiCl = 613 °C, LiBr = 547 °C, LiI = 446 °CIt is found that the greater the possibility of polarization, the lower is the melting point and heat of sublimation and the greater is the solubility in non-polar solvents.Percentage of ionic character and charge distributionBased on Fajan's rules, it is expected that every ionic compound will have at least some amount of covalent character. The percentage of ionic character in a compound can be estimated from dipole moments.The bond dipole moment uses the idea of electric dipole moment to measure the polarity of a chemical bond within a molecule. It occurs whenever there is a separation of positive and negative charges. The bond dipole μ is given by:μ = δ dA bond dipole is modeled as +δ - δ- with a distance d between the partial charges. It is a vector, parallel to the bond axis and by convention points from minus to plus (note that many texts appear to ignore the convention and point from plus to minus). The SI unit for an electric dipole moment is the coulomb-meter, (C m). This is thought to produce values too large to be practical on the molecular scale so bond dipole moments are commonly measured in Debye, represented by the symbol, D.Question. Enumerate factors affecting resistivity and discuss them.Answer: Then the factors which affect the resistance (R) of a conductor in ohms can be listed as:● The resistivity (ρ) of the material from which the conductor is made.● The total length (L) of the conductor.● The cross-sectional area (A) of the conductor.● The temperature of the conductor.TemperatureThe resistivity of materials changes with temperature. Resistivity of most of the metals increase with temperature. The change in the resistivity of material with change in temperature is given by formula given below-

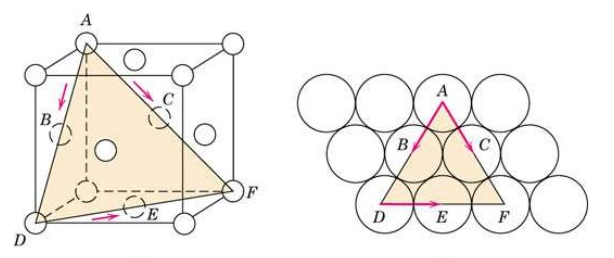
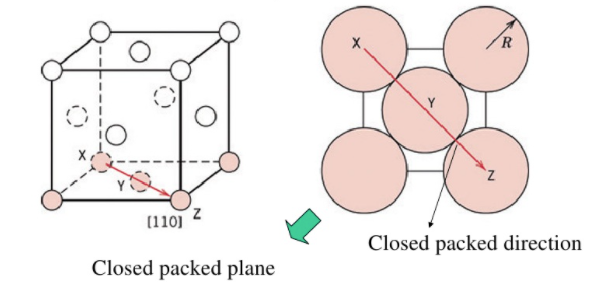
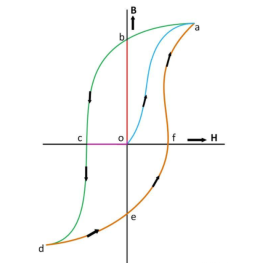
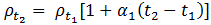Where,ρt1 is the resistivity of material at temperature of t1o Candρt2 is the resistivity of material at temperature of t2oCα1 is temperature coefficient of resistance of material at temperature of t1o C.If the value of α1 is positive, the resistivity of material is increase.The resistivity of metals increase with increase of temperature. Means the metals are having positive temperature coefficient of resistance. Several metals exhibit the zero resistivity at temperature near to absolute zero. This phenomenon is “called the superconductivity”. The resistivity of semiconductors and insulators decrease with increase in temperature. Means the semiconductors and insulators are having negative temperature coefficient of resistance.AlloyingAlloying is a solid solution of two or more metals. Alloying of metals is used to achieve some mechanical and electrical properties. The atomic structure of a solid solution is irregular as compared to pure metals. Due to which the electrical resistivity of the solid solution increases more rapidly with increase of alloy content. A small content of impurity may increase the resistivity metal considerably. Even the impurity of low resistivity increases the resistivity of base metal considerably. For example the impurity of silver (having lowest resistivity among all metals) in copper increase the resistivity of copper.Mechanical StressingMechanical stressing of the crystal structure of material develops the localized strains in the material crystal structure. These localized stains disturb the movement of free electrons through the material. Which results in an increase in resistivity of the material. Subsequently, annealing, of metal reduces the resistivity of metal. Annealing of metal, relieve the mechanical stressing of material due to which the localized stains got removed from the crystal structure of the metal. Due to which the resistivity of metal decrease. For example, the resistivity of hard drawn copper is more as compared to annealed copper.Age HardeningAge hardening is a heat treatment process used to increase the yield strength and to develop the ability in alloys to resist the permanent deformation by external forces. Age hardening is also called “Precipitation Hardening”. This process increases the strength of alloys by creating solid impurities or precipitate. These created solid impurities or precipitate, disturb the crystal structure of metal which interrupts the flow of free electrons through metal/Due to which the resistivity of metal increases.Cold WorkingCold working is a manufacturing process used to increase the strength of metals. Cold working is also known as “Work hardening” or “Strain hardening”. Cold working is used to increase the mechanical strength of the metal. Cold working disturbs the crystal structure of metals which interfere with the movement of electrons in metal, due to which the resistivity of metal increases.Question. What is magnetic hysteresis? Enumerate the application of magnetic materials based on hysteresis characteristics Answer: The phenomenon of flux density B lagging behind the magnetizing force H in a magnetic material is known as Magnetic Hysteresis. The word Hysteresis is derived from the Greek word Hysterein means to lag behind.When the magnetic material is magnetized first in one direction and then in the other direction, completing one cycle of magnetization, it is found that the flux density B lags behind the applied magnetization force H.There are various types of magnetic materials such as paramagnetic, diamagnetic, ferromagnetic, ferromagnetic and antiferromagnetic materials. Ferromagnetic materials are mainly responsible for the generation of the hysteresis loop.

When the magnetic field in not applied the ferromagnetic material behaves like a paramagnetic material. This means that at the initial stage the dipole of the ferromagnetic material is not aligned, they are randomly placed.As soon as the magnetic field is applied to the ferromagnetic material, its dipole moments align themselves in one particular direction as shown in the above figure, resulting in a much stronger magnetic field.For understanding the phenomenon of the magnetic hysteresis, consider a ring of magnetic material wound uniformly with solenoid. The solenoid is connected to a DC source through a Double pole double throw (D.P.D.T) reversible switch as shown in the figure below:

Initially, the switch is in position 1. By decreasing the value of R the value of the current in the solenoid increases gradually resulting in a gradual increase in field intensity H, the flux density also increases till it reaches the saturation point a and the curve obtained is ‘oa‘. Saturation occurs when on increasing the current, dipole moment or the molecules of the magnet material align itself in one direction.Now by decreasing the current in the solenoid to zero the magnetizing force is gradually reduced to zero. But the value of flux density will not be zero as it still has the value ‘ob‘when H=0, so the curve obtained is ‘ab‘as shown in the figure below. This value ‘ob‘of flux density is because of the residual magnetism

Applications of magnetic hysteresis are:As magnetic substances have an extended range of hysteresis loop, these are implemented in the devices such as

● Hard disk

● Audio recording devices

● Magnetic tapes

● Credit cards

Also, there exists constricted magnetic hysteresis loop substances and these are used in

● Transformers

● Solenoids

● Electromagnets

● Relays

Employed in damping the angular motion of satellites in the minimal earth orbit as because of the advent of the space age.Question. Explain the effect of temperature on the magnetic behaviour of different types of magnetic materialsAnswer: All magnetic materials experience a change in flux density as their temperature increases and decreases from an ambient temperature. For example, most magnets with the exception of ferrite will actually display an increase in strength as the temperature drops and all permanent magnets (including ferrite) will lose a percentage of their performance for every degree increase. Whether this lost performance is recovered on cooling depends on the materials maximum operating temperature and the temperature the magnet is exposed to.Reversible lossReversible loss occurs for every degree rise in temperature the magnet experiences above ambient, up to its maximum operating temperature. As the magnet cools, the performance returns to the previous level.Irreversible lossWhen a magnet is heated above its maximum operating temperature but below its Curie temperature, it will experience irreversible losses in performance. This means if the magnet is then cooled, its performance will be weaker than it was before it was heated. A magnet that has experienced irreversible loss could theoretically be remagnetised back to its original strength, but this is not a cost effective process. Irreversible loss is a result of the elevated temperature reversing the magnetization of single individual magnetic domains. This means that irreversible loss happens just once; if the same thermal cycle is repeated no additional loss will occur as each individual domain can only be reversed once after it is magnetised.Permanent lossPermanent loss of magnetic performance is experienced when a magnet is heated above its Curie temperature. At this point the structure of the magnetic domains change and become self-keepering, resulting in permanent magnetic damage which cannot be repaired by remagnetisation.The Curie temperature of permanent magnetic materials is often quoted on datasheets, but when taken in isolation this is often the least useful thermal characteristic when designing an application as no design should function close to these extreme high temperatures. Therefore, other parameters such as maximum operating temperature should be considered.Neodymium magnets?The degree change in performance for a neodymium magnet depends on its shape and the design of the circuit within which it used, e.g. whether it is in ‘free space’ or whether it is connected to a steel surface. Small, thin magnets will generally be more susceptible than magnets greater in volume to rising temperatures. That considered, all neodymium magnets will lose a certain amount of performance for every degree rise in temperature even if the temperature is below their maximum operating temperature. In fact, depending on size, shape, grade and how it is used, a neodymium magnet will lose 0.08%-0.12% of its magnetic strength for every degree Celsius rise in temperature.Up to 150 degrees Celsius neodymium magnets are considered to have the best magnetic performance of all permanent magnetic materials, but when elevated to temperatures above 150 degrees Celsius their magnetic strength will be reduced below that of a magnet of the same size magnet made from samarium cobalt material. Neodymium magnets maintain their magnetic stability in very low temperatures; only at -138 degrees Celsius will their magnetic structure become affected. At this point, a neodymium magnet’s direction of magnetism will alter, resulting in a loss of performance between 10 and 20%.Standard grade neodymium magnets have a maximum operating temperature of 80 degrees Celsius. When heated above this, they will experience irrecoverable losses in performance. High temperature grades of neodymium magnets with higher maximum operating temperatures are available and these are identified by a suffix after the name of the standard grade.Samarium cobalt magnetsSamarium cobalt magnets are not as strong as neodymium magnets at room temperature but have a better temperature coefficient for both remanence (Br) and resistance to demagnetization (Hci) than neodymium magnets. For example, once the temperature exceeds 150 degrees Celsius, samarium cobalt magnets outperform neodymium magnets and standard grades of samarium cobalt (Sm2Co17) magnets will not suffer irrecoverable losses until the temperature exceeds 350 degrees Celsius.Alnico magnetsAlnico magnets are characterised by their high remanence but low coercivity, which means that they are second only to neodymium magnets in terms of magnetic strength, but are significantly more susceptible to demagnetisation by external magnetic fields and physical shock, although not by elevated temperature. In fact, of all permanent magnetic materials, alnico magnets have the greatest thermal stability only losing a fraction (0.02%) of their performance for every degree Celsius rise in temperature above ambient. Alnico magnets also have the highest maximum operating temperature of all the permanent magnet family, not suffering irreversible losses in performance until the temperature reaches 525 degrees C (alnico5).Ferrite magnetsUnique among permanent magnets, ferrite magnets actually become more resistant to demagnetization as their temperature increases. Conversely, their strength decreases as their temperature rises, albeit at a lower rate. These characteristics make them particularly popular for high temperature applications such as electric motors and generators. The intrinsic coercivity of a ferrite magnet (resistance to demagnetisation) increases by 0.4% per degree rise in temperature, while their magnetic strength decreases by 0.2% for each degree Celsius increase. Ferrite magnets can be used in temperatures up to 180 degrees Celsius before they will begin to experience irreversible losses in performance.Question. Describe the importance of single-crystalline semiconductor Answer: Mostly single crystals of semiconductors, dielectrics, metals, or alloys are produced in the process of crystallization or solidification from the melt. The rates of crystallization can reach tens of millimeters per minute. During crystallization in single crystals, structural defects can be collected that have a negative effect on the mechanical and other properties of materials. High demands for structural perfection and chemical purity of single crystals caused considerable research efforts aimed at the study and improvement of the main techniques of growing single crystals from the melt (Czochralski, Stepanov, Bridgman, Verneuil, and floating zone). Single crystals of refractory bcc metals, especially molybdenum and tungsten, are widely used in several areas of modern technology, such as nuclear energy, electronics, lighting fixtures, mainly for the manufacture of parts and devices (anodes, cathodes, etc.) working at high temperatures. A scope of single crystals of refractory metals is continuously expanding, and requirements for chemical purity of crystals, their structural quality and geometry are constantly growing. Currently, the most pure single crystals of molybdenum and tungsten, as well of a number of other refractory metals can be produced by electron-beam floating zone melting (EBFZM). However, their crystallographic perfection due to the specific features of the floating zone method with electron-beam heating, often no longer satisfies the developers of new instruments and devices. A characteristic blocky structure and a high density of dislocations make such crystals unsuitable, for example, for research of channeling high-energy particles or posing a number of other subtle physical experiments. Further increase in a degree of purity and crystallographic perfection of single crystals of refractory metals is closely related to a development of theoretical and experimental researches of crystallization processes, the development of new apparatuses and methods for producing single crystals, as well as optimization of known processes. Therefore, to obtain additional information about the laws of formation of a dislocation structure, an impact on specific parameters of crystal growth in the floating zone method seems to be a relevant scientific and technical challenge. The basis of this decision is a study of peculiarities of structural defects in single crystals grown by crystallization, which is one of the fundamental problems of solid state physics, physical chemistry, and theory of phase transitions.Shaped tungsten single crystals are used as screens of different shapes, inputs, crucibles, shapers and other products. There is considerable interest in profiled tubular shaped single crystals (primarily, of tungsten) in connection with their use in prospective designs of thermionic converters. The production of tubular tungsten single crystals from bulk cylindrical crystals by traditional machining (drilling, broaching) is extremely labor-intensive, low-tech and uneconomical. Getting such tubes pulled from the melt, for example, by Stepanov method, is impossible even for the reason that there are no available materials for the shaper. The only possibility to obtain single-crystalline tungsten tubes by crystallization from the melt is to use for this purpose the EBFZM method. Various materials can be successfully applied in industry to create structures, machine parts and devices only if they can be given in the required shape. Such shaping of crystalline materials may be done of the solid material (rolling, forging, shaping by cutting, etc.) and liquid phase (casting, welding). The shaping methods are now widely used to obtain polycrystalline products. Recently, in science and technology becoming more widely used are single crystals in the form of plates, tubes, rods of various sizes. In principle, the single-crystalline tube may be cut out from a bulk single crystal by mechanical or electrical discharge machining. However, using such kinds of processing, the single crystal will inevitably contain multiple structural defects that can alter the properties of the crystal in an unpredictable manner. For example, during the electroerosion cut of tungsten single crystals a network of cracks in the sub-surface layer occurs, and the dislocation density increases. Furthermore, such treatments are inefficient; too much waste material is usually lost. The low economic efficiency and non-technological methods have led to search for alternative methods of getting profiled single crystals. Among them are plastic deformation, epitaxial growth from the gaseous phase, crystallization from a molten solution, crystallization from the melt. Advantages of the latter forming method consist mainly in the higher productivity and better quality (because of both the structure and properties) of the final product. Crystallization from the melt provides the most perfect structure and high purity of single crystals because of the contact-less melting with no contaminating material at the front of crystallization (e.g., Czochralski method). However, due to the low stability of the capillary shaping this method can allows obtaining only products of the simplest form – the rods. Verneuil method, including plasma heating, allows obtaining single crystals of various materials in the form of tubes. It seems that the most suitable method for obtaining the tubular single crystals by crystallization from the melt is Stepanov method. The method consists in a capillary shaping of the column from the melt using a special shaper and its crystallization proceeds outside the container with the melt. The Stepanov method has a significant margin of stability and enables the profiled metal and semiconductor crystals of high quality. A float zone method can also be used for crystallization of single crystal tubes from the melt. An example of using this method to obtain tubes can be found in the monograph. In principle, the float zone methods may use any heating source, but the most suitable method to obtain the tungsten tubular single crystals with thin walls is floating zone method with electron-beam heating. Until now, by the method of EBFZM from the melt were grown the most perfect and the purest single crystals of tungsten and other refractory metals. Crystals obtained by this method typically have a cylindrical shape. EBFZM method seems to be the most promising for growing shaped single crystals of tungsten and other refractory metals in the form of tubes. Growing tubular crystals of tungsten was done on the set-up for EBFZM. Tungsten tubular feeds which were produced by CVD had an outer diameter of 16 mm and a wall thickness of 1.5 mm (a diameter of feeds varies from 10 to 22 mm). Seeds for growing single crystals were cut from the tubular cylindrical tungsten single crystals with the growth axis [111] and [001] by electro erosion, followed by removal of the damaged layer.Question. How can single crystal be produced? Explain any one technique in detail.Answer: For growing oriented single crystals of semiconductors and dielectrics, the Czochralski method became widespread. The essence of the method consists in pulling of single crystals by seeding at a surface of the melt. Although this method of capillary formation is known by its low stability, at high precision heating control and automation of pulling it allows obtaining such semiconductors as silicon and germanium which are widely used in modern technology. Bridgman method, which also refers to the crucible methods similar to Czochralski, is used in a much smaller scale and mostly for growing single crystals of low-temperature melting metals. This is due to the fact that at high temperatures there are significant difficulties in finding materials for crucibles. Another widely used technique is the Stepanov method of growing single crystals. Its difference from Czochralski consists in that the shaper is immersed into the melt, providing not only pulling cylindrical rods, but also production of a wide assortment of shaped crystals (tapes, tubes, polyhedrons, and other crystals of a complex shape). The Stepanov method has much greater margins of stability during capillary shaping than Czochralski, which accounts for its wide distribution. However, for growing single crystals of refractory metals, especially molybdenum and tungsten, the above-mentioned methods are not suitable, as the high melting temperature and high chemical reactivity of liquid refractory metals do not allow obtaining them by any crucible method. The actual process of the growth is desirable to maintain in a vacuum or in an inert gas. For refractory metals Verneuil method is also used provided with another kind of a heater as plasma. This method yielded the most by large-scale tungsten single crystals of 40 mm in diameter and weighing up to 10 kg. However, those single crystals were of poor structural quality and had high gas content, especially of a plasma gas. The most perfect single crystals of refractory metals can be obtained by electron-beam floating zone melting. The growth of these crystals is characterized by the fact that the method is a crucible-less one and a melt has no any contact with other materials. The melt is supported by forces of surface tension and the process is carried out in UHV. A phase diagram can give information on the type, number and volume fraction of phases at crystal growing from the melt. This is true only in the case when crystallization proceeds at an infinitesimal rate. In practice, a finite rate and solidification conditions are far from thermodynamic equilibrium. Thus, binary alloy solidification occurs with enrichment or depletion of solid with a dissolved component. When impurity accumulation exceeds some critical value and a temperature gradient in liquid is reduced below a critical level, there comes concentration supercooling and the interphase surface changes from cellular to dendritic. This is nonequilibrium solidification and is typical of most alloys. A main feature of such solidification is that a primary axis of dendrites is strictly parallel to a heat flow direction and interdendritic spaces are enriched with impurities. This segregation further can be partially eliminated by prolonged high-temperature annealing. In some cases, there may be precipitates of a second phase in interdendritic spaces. When crystal growth conditions are such that a part of a two-phase zone is large and a growth rate is high, so that the factor is a lot less than zero: G−V(FR)eff (1/D) ≪0, G-VFReff(1/D) ≪0, where, G the temperature gradient in fluid; V the growth rate; (FR)eff the effective solidification range; D the diffusion coefficient. Thus, there is a porosity which may occur even in growing single crystals of pure refractory metals by EBFZM. It occurs especially after the first liquid zone passage during purifying the initial PM feed and growing a single crystal from. EBFZM provides not only a given orientation of crystal growth, but also due to refining by a zone effect mainly from substitution impurities. Refining of interstitial impurities occurs mainly by vacuum evaporation, the more that the melting points of refractory metals are very high. Impurities in a growing crystal often are undesirable as adversely affecting its structure and properties. In the process of accumulation of impurities before moving crystallization front, the plane crystallization front may become unstable due to the so-called phenomenon of concentration supercooling. Impurities will greatly impair the dislocation substructure and are unevenly distributed in a radial direction and a length of the crystal along the growth axis.Question. What is Hall Effect? Derive an expression for Hall Effect in semiconductors.Answer: Hall Effect is defined as the production of a voltage difference across an electrical conductor which is transverse to an electric current and with respect to an applied magnetic field it is perpendicular to the current. Edwin Hall discovered this effect in the year 1879.Hall field is defined as the field developed across the conductor and Hall voltage is the corresponding potential difference. This principle is observed in the charges involved in the electromagnetic fields.Consider a metal with one type charge carriers that are electrons and is a steady-state condition with no movement of charges in the y-axis direction. Following is the derivation of Hall-effect: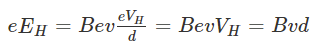

(at equilibrium, force is downwards due to magnetic field which is equal to upward electric force)Where,VH is Hall voltageEH is Hall fieldv is the drift velocityd is the width of the metal slabB is the magnetic fieldBev is a force acting on an electron

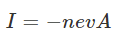Where,I is an electric currentn is no.of electrons per unit volumeA is the cross-sectional area of the conductor

Where,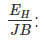

Hall coefficient (RH) is defined as the ratio between the induced electric field and the product of applied magnetic field and current density. In semiconductors, RH is positive for the hole and negative for free electrons.

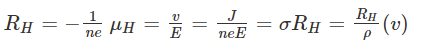Where,E is an electric fieldv is the drift velocityRH is the Hall coefficient𝛍H is the mobility of the hole

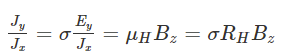The ratio between density (x-axis direction) and current density (y-axis direction) is known as the Hall angle that measures the average number of radians due to collisions of the particles.

Where,R is Hall resistanceIn semiconductors, electrons and holes contribute to different concentrations and mobilities which makes it difficult for the explanation of the Hall coefficient given above. Therefore, for the simple explanation of a moderate magnetic field, the following is the Hall coefficient: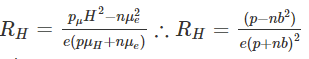

where,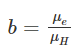

● n is electron concentration

● p is hole concentration

● 𝛍e is the mobility of electron

● 𝛍H is the mobility of the hole

● e is an elementary charge

Question. What is superconductivity and its importance in engineering? Name few high-temperature superconductorsAnswer: Some materials when they are cooled, below certain temperature their resistivity get abolished means they exhibit the infinite conductivityThe temperature at which the metals change from normal conducting state to superconducting state, is called critical temperature/transition temperature. An example of superconductors, is Mercury. It becomes superconductor at 4k. In superconducting state the materials expel the magnetic field.

The transition from normal conducting state to superconducting state is reversible. Moreover, below critical temperature the superconductivity can be abolished either by passing sufficient large current through conductor itself or by applying sufficient strong external magnetic field. Below critical temperature/transition temperature, the value of current through conductor itself at which the superconducting state abolished is called critical current. As the temperature (below the critical temperature) reduces the value of critical current increase. The value of critical current increase with decrease in temperature. The value of critical magnetic field also depends on temperature. As the temperature (below the critical temperature) reduces the value of critical magnetic field increase.Films of the new materials can carry currents in the superconducting state that are large enough to be of importance in making many devices. Possible applications of the high-temperature superconductors in thin-film or bulk form include the construction of computer parts (logic devices, memory elements, switches, and interconnects), oscillators, amplifiers, particle accelerators, highly sensitive devices for measuring magnetic fields, voltages or currents, magnets for medical magnetic-imaging devices, magnetic energy-storage systems, levitated passenger trains for high-speed travel, motors, generators, transformers, and transmission lines. The principal advantages of these superconducting devices would be their low power dissipation, high operating speed, and extreme sensitivity.Equipment made with the high-temperature superconductors would also be more economical to operate because such materials can be cooled with inexpensive liquid nitrogen (boiling point, 77 K) rather than with costly liquid helium (boiling point, 4.2 K). The ceramics have problems, however, which must be overcome before useful devices can be made from them. These problems include brittleness, instabilities of the materials in some chemical environments, and a tendency for impurities to segregate at surfaces and grain boundaries, where they interfere with the flow of high currents in the superconducting state.Question. Explain BCS theory for super conductivity.Answer: An intuitive description of superconductivity is sufficient for public and non-technical uses. However, ultimately, a more rigorous mathematically- based explanation must be formulated. Superconductivity was not sufficiently explained until 1957 when John Bardeen and his graduate assistants Leon Cooper and John Schrieffer proposed a microscopic explanation that would later be their namesake: the BCS Theory. This theoretical explanation later earned them the Nobel Prize, making John Bardeen the only man in history to be awarded this honor twice.The BCS Theory is, in its simplest form, actually contradictory to our crude macroscopic view expressed earlier. As discussed earlier, superconductivity arises because electrons do not interact destructively with atoms in the crystal lattice of the material. The BCS Theory says that electrons do actually interact with the atoms, but constructively.The BCS Theory makes a crucial assumption at the beginning: that an attractive force exists between electrons. In typical Type I superconductors, this force is due to Coulomb attraction between the electron and the crystal lattice. An electron in the lattice will cause a slight increase in positive charges around it. This increase in positive charge will, in turn, attract another electron. These two electrons are known as a Cooper pair. If the energy required to bind these electrons together is less than the energy from the thermal vibrations of the lattice attempting to break them apart, the pair will remain bound. This explains (roughly) why superconductivity requires low temperatures- the thermal vibration of the lattice must be small enough to allow the forming of Cooper pairs. In a superconductor, the current is made up of these Cooper pairs, rather than individual electrons.So, Cooper pairs are formed by Coulomb interactions with the crystal lattice. This is also what overcomes resistance. Remember, an electron inside the lattice causes a slight increase of positive charge due to Coulomb attraction. As the Cooper pair flows, the leading electron causes this increase of charge, and the trailing electron is attracted by it. This is illustrated below.

This BCS theory prediction of Cooper pair interaction with the crystal lattice has been verified experimentally by the isotope effect. That is, the critical temperature of a material depends on the mass of the nucleus of the atoms. If an isotope is used (neutrons are added to make it more massive), the critical temperature decreases. This effect is most evident in Type I, and appears only weakly in Type II.This superconductivity of Cooper pairs is somewhat related to Bose-Einstein Condensation. The Cooper pairs act somewhat like bosons, which condense into their lowest energy level below the critical temperature, and lose electrical resistance.The BCS Theory did exactly what a physical theory should do: it explained properties already witnessed in experiment, and it predicted experimentally verifiable phenomena. Though its specific quantitative elements were quite limited in their application (it only explained Type I s-wave superconductivity), its essence was quite broad and has been modified and applied to various other superconductors, such as Type II perovskites.Question. Differentiate the following:a) Fluorescence and PhosphorescenceOne radiative mechanism by which excited electrons may relax is a light-emitting transition from the lowest excited state (S1) to ground state (S0) in a fast (10-9 to 10-6 sec) process called fluorescence. The energy difference is dissipated by emitting a photon. Due to the electron having shed some of the original excitation energy by vibrational relaxation, the emitted photon will be of lower energy and thus of longer wavelength.Similar to excitation, emission may generally relax to a variety of vibrational levels (v=n) of the ground state (S0), resulting in a bandwidth of possible wavelengths of the emitted photon. Electrons relax from higher vibrational levels (v=n) further to vibration less state (v=0) by non-radiative vibrational relaxation, if necessary. The resulting emitted wavelength is independent of the excitation wavelength, as usually excited molecules decay to the lowest vibrational level of the lowest excited state by non-radiative processes before fluorescence emission takes place. Depending on the molecule, non-radiative decay might be responsible for dissipating a smaller or bigger portion of the excitation energy, resulting in molecule-specific shifts between the excitation wavelengths and the wavelengths being emitted. This phenomenon is termed Stokes shift. The possible wavelength of a photon that might be absorbed in the excitation, as well as the possible emitted wavelengths –which vary due to fluorescent decay onto different vibrational levels– define together a molecule’s excitation and emission spectra. As frequently the same electronic transitions are involved in excitation and emission of a fluorescent molecule, the excitation and emission spectra often resemble reflections of each other, which is referred to as the mirror image rule of fluorescence.Spin is a fundamental, unvarying property of the electron and a form of angular momentum that defines behavior in an electromagnetic field. Electron spin can only have the value of ½ and the spin orientation is either up or down. An electron’s spin is therefore designated as +½ or -½, or alternatively as ↑ or↓. Two electrons in a single orbital will always have antiparallel spin at singlet ground state (S0). Upon promotion of one electron into excited state, the electron maintains its spin orientation and a singlet excited state (S1) is formed, where the both spin orientations remain paired as antiparallel. All relaxation events in fluorescence are spin neutral and the spin orientation of the electron is maintained at all times.However, this is different for phosphorescence. Fast (10-11 to 10-6 sec) Intersystem crossing from singlet exited state (S1) to an energetically favorable triplet excited state (T1) leads to inversion of the electron spin. Triplet excited states are characterized by parallel spin of both electrons and are metastable. Relaxation occurs via phosphorescence, which results in another flip of the electron spin and the emittance of a photon. The return to relaxed singlet ground state (S0) might occur after considerable delay (10-3 to >100 sec). Additionally, more energy is dissipated by non-radiative processes during phosphorescent relaxation than in fluorescence, therefore the energy difference between the absorbed and emitted photon is bigger and the wavelength shift more pronounced. Thus, phosphorescence is characterized by a bigger Stokes shift than fluorescence.b) Type-1 and Type-II superconductors

Type – I Superconductors

Type – II Superconductors

Low critical temperature (typically in the range of 0K to 10K)

High critical temperature (typically greater than 10K)

Low Critical magnetic field (Typically in the range of 0.0000049 T to 1T)

High Critical magnetic field (Typically greater than 1T)

Perfectly obey the Meissner effect: Magnetic field cannot penetrate inside the material.

Partly obey the Meissner effect but not completely: Magnetic field can penetrate inside the material.

Exhibits single critical magnetic field.

Exhibits two critical magnetic field

Easily lose the superconducting state by low-intensity magnetic field. Therefore, type-I superconductors are also known as soft superconductors.

Does not easily lose the superconducting state by external magnetic field. Therefore, type-II superconductors are also known as hard superconductors.

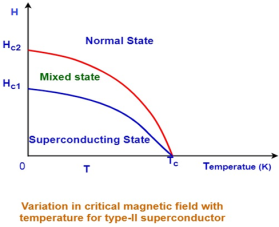
The transition from a superconducting state to a normal state due to the external magnetic field is sharp and abrupt for type-I superconductors.

The transition from a superconducting state to a normal state due to the external magnetic field is gradually but not shape and abrupt. At lower critical magnetic field (HC1), type-II superconductor starts losing its superconductivity. At upper critical magnetic field (HC2), type-II superconductor completely loses its superconductivity. The state between lower critical magnetic field and upper magnetic field is known as an intermediate state or mixed state.

Due to the low critical magnetic field, type-I superconductors cannot be used for manufacturing electromagnets used for producing strong magnetic field.

Due to the high critical magnetic field, type-II superconductors can be used for manufacturing electromagnets used for producing strong magnetic field.

Type-I superconductors are generally pure metals.

Type-II superconductors are generally alloys and complex oxides of ceramics.

BCS theory can be used to explain the superconductivity of type-I superconductors.

BCS theory cannot be used to explain the superconductivity of type-II superconductors.

These are completely diamagnetic.

These are not completely diamagnetic

These are also called as Soft Superconductors.

These are also called as Hard Superconductors.

These are also called as Low-temperature Superconductors.

These are also called as High-temperature Superconductors.

No mixed state exists in type-I Superconductors.

A mixed state exists in type-II Superconductors.

Slight impurity does not affect the superconductivity of type-I superconductors.

Slight impurity greatly affects the superconductivity of type-II superconductors.

Due to the low critical magnetic field, type-I superconductors have limited technical applications.

Due to the high critical magnetic field, type-II superconductors have wider technical applications.

Examples: Hg, Pb, Zn,etc.

Examples: NbTi, Nb3Sn, etc.

c) n-type and p-type semiconductors

BASIS OF DIFFERENCE	p- TYPE SEMICONDUCTOR	n- TYPE SEMICONDUCTOR
Group of Doping Element	In P type semiconductor III group element is added as doping element.	In n type semiconductor V group elements are added as doping elements.
Nature of Doping Element	Impurity added creates vacancy of electrons (holes) called as Acceptor Atoms.	Impurity added provides extra electrons and is known as the Donor Atom.
Type of impurity added	Trivalent impurity like Al, Ga, In etc. are added.	Pentavalent impurity like P, As, Sb, Bi etc. are added.
Majority Carriers	Holes are majority carriers	Electrons are majority carriers
Minority Carriers	Electrons are minority carriers	Holes are minority carriers
Density of Electrons and Holes	The hole density is much greater than the electron density. nh >> ne	The electron density is much greater than the hole density. ne >> nh
Energy level	The acceptor energy level is close to the valence band and away from the conduction band.	The donor energy level is close to the conduction band and away from the valence band.
Fermi level	Fermi level lies between acceptor energy level and the valence band.	Fermi level lies between donor energy level and the conduction band.
Movement of Majority carriers	Majority carriers move from higher to lower potential.	Majority carriers move from lower to higher potential.

Question. Write a short notes on the following:a) Meissner effectMeissner effect, the expulsion of a magnetic field from the interior of a material that is in the process of becoming a superconductor, that is, losing its resistance to the flow of electrical currents when cooled below a certain temperature, called the transition temperature, usually close to absolute zero.As a superconductor in a magnetic field is cooled to the temperature at which it abruptly loses electrical resistance, all or part of the magnetic field within the material is expelled. Relatively weak magnetic fields are entirely repulsed from the interior of all superconductors except for a surface layer about one-millionth of an inch thick. The external magnetic field may be made so strong, however, that it prevents a transition to the superconducting state, and the Meissner effect does not occur.Generally, ranges of intermediate magnetic-field strengths, which are present during cooling, produce a partial Meissner effect as the original field is reduced within the material but not wholly expelled. Some superconductors, called type I (tin and mercury, for example), can be made to exhibit a complete Meissner effect by eliminating various chemical impurities and physical imperfections and by choosing proper geometrical shape and size. Other superconductors, called type II (vanadium and niobium, for example), exhibit only a partial Meissner effect at intermediate magnetic-field strengths no matter what their geometrical shape or size. Type II superconductors show decreasing expulsion of the magnetic field as its strength increases until they abruptly cease being superconductors in relatively strong magnetic fields.b) Dielectric lossesDielectric loss, loss of energy that goes into heating a dielectric material in a varying electric field. For example, a capacitor incorporated in an alternating-current circuit is alternately charged and discharged each half cycle. During the alternation of polarity of the plates, the charges must be displaced through the dielectric first in one direction and then in the other, and overcoming the opposition that they encounter leads to a production of heat through dielectric loss, a characteristic that must be considered when applying capacitors to electric circuits, such as those in radio and television receivers. Dielectric losses depend on frequency and the dielectric material. Heating through dielectric loss is widely employed industrially for heating thermosetting glues, for drying lumber and other fibrous materials, for preheating plastics before molding, and for fast jelling and drying of foam rubber.c) Manufacturing techniques of PCBsThe PCB manufacturing process is very important for anyone involved in the electronics industry. Printed circuit boards, PCBs, are very widely used as the basis for electronic circuits. Printed circuit boards are used to provide the mechanical basis on which the circuit can be built. Accordingly virtually all circuits use printed circuit boards and they are designed and used in quantities of millions.Although PCBs form the basis of virtually all electronic circuits today, they tend to be taken for granted. Nevertheless technology in this area of electronics is moving forward. Track sizes are decreasing, the numbers of layers in the boards is increasing to accommodate for the increased connectivity required, and the design rules are being improved to ensure that smaller SMT devices can be handled and the soldering processes used in production can be accommodated.The PCB manufacturing process can be achieved in a variety of ways and there are a number of variants. Despite the many small variations, the main stages in the PCB manufacturing process are the same.Printed circuit boards, PCBs, can be made from a variety of substances. The most widely used in a form of glass fibre based board known as FR4. This provides a reasonable degree of stability under temperature variation and is does not breakdown badly, while not being excessively expensive. Other cheaper materials are available for the PCBs in low cost commercial products. For high performance radio frequency designs where the dielectric constant of the substrate is important, and low levels of loss are needed, then PTFE based printed circuit boards can be used, although they are far more difficult to work with.In order to make a PCB with tracks for the components, copper clad board is first obtained. This consists of the substrate material, typically FR4, with copper cladding normally on both sides. This copper cladding consists of a thin layer of copper sheet bonded to the board. This bonding is normally very good for FR4, but the very nature of PTFE makes this more difficult, and this adds difficulty to the processing of PTFE PCBs. With the bare PCB boards chosen and available the next step is to create the required tracks on the board and remove the unwanted copper. The manufacture of the PCBs is normally achieved using a chemical etching process. The most common form of etch used with PCBs is ferric chloride.In order to gain the correct pattern of tracks, a photographic process is used. Typically the copper on the bare printed circuit boards is covered with a thin layer of photo-resist. It is then exposed to light through a photographic film or photo-mask detailing the tracks required. In this way the image of the tracks is passed onto the photo-resist. With this complete, the photo-resist is placed in a developer so that only those areas of the board where tracks are needed are covered in the resist.The next stage in the process is to place the printed circuit boards into the ferric chloride to etch the areas where no track or copper is required. Knowing the concentration of the ferric chloride and the thickness of the copper on the board, it is placed into the etch froth e required amount of time. If the printed circuit boards are placed in the etch for too long, then some definition is lost as the ferric chloride will tend to undercut the photo-resist.Although most PCB boards are manufacturing using photographic processing, other methods are also available. One is to use a specialised highly accurate milling machine. The machine is then controlled to mill away the copper in those areas where the copper is not required. The control is obviously automated and driven from files generated by the PCB design software. This form of PCB manufacture is not suitable for large quantity but it is an ideal option in many instances where very small quantities of a PCB prototype quantities are needed.Another method that is sometimes used for a PCB prototype is to print etch resistant inks onto the PCB using a silk screening process.

Sign Up