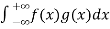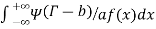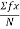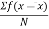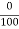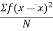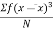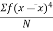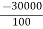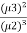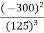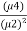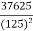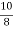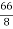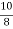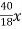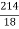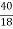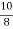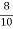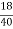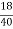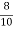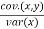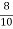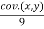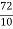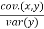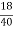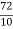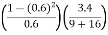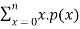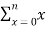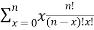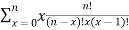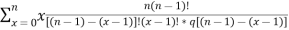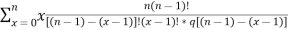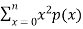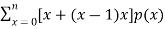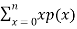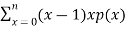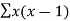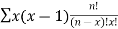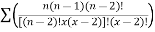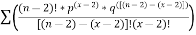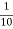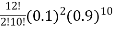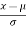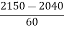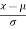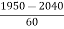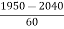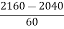Q (1) A) what is the Wavelet transform? Wavelet transform:-- In mathematics, a wavelet series is a representation of a square – integrable function by a certain ortho normal series generated by a wavelet. A function y Î L2 is called an orthonormal wavelet if it can be used to define a Hilbert basis that is a complete orthonormal system. For the Hilbert space L2 (R) of square integrable function. The Hilbert basis is constructed as the family of Function {yjk : j, k Î z } yjk(x) = 2j/2 y(2j x – k ) for integers j,k Î z If under the standard inner product on L2(R) (f,g) = this family is orthonormal Completeness is satisfied if every function f ÎL2(R) may be expanded in the basis of f(x) = with convergence of the series understood to be convergence in norm. Such a representation of f is known as a wavelet series. The integral wavelet transform is defined as [Wyf] (a,b) = 1/Ö|a| The wavelet coefficient Cj,k are then given by Cj,k = [Wyf] (2-j , k2-j) Here, a = 2-j is called the binary dilation & b = k2-j is the binary position |
Q (2) B) For any three sets A, B, C prove that A x (B U C) = (AxB)U(AxC) Answer: To prove : A * (B U C) = ( A * B) U ( A * C) Proof : Let (a, b) Î A * (B U C) => a Î A and b Î (B U C) => a ÎA and { b Î B or b Î C} => {a Î A and b Î B } or {a Î A and b Î C } => (a,b) Î ( A * B) U ( A * C) \ (a, b) Î A * (B U C) => (a,b) Î ( A * B) U ( A * C) \ A * (B U C) Í ( A * B) U ( A * C) -------------------------(1) Again , Let (x,y) Î( A * B) U ( A * C) => (x,y) Î( A * B) or (x,y) Î( A * C) => {x Î A and y Î B} or {x Î A and y Î C} => x Î A and y Î (B U C) => (x,y) Î A * (B U C) \ (x,y) Î( A * B) U ( A * C) = (x,y) Î A * (B U C) \ ( A * B) U ( A * C) Í A * (B U C) ------------------------------(2) Now from equation (1) & (2) we get, Hence,
|
Q (3) A)Discuss Skewness and Kurtosis for the following frequency distribution:
Answer: skewness of kurtosis : Step 1: - To find mean x
\ x =
Step 2 : - To find central Moments :
m1 = m2 = m3 = m4 =
skewness b1 =
b1 ¹ 0 Hence distribution is unsymmetrical b2 = = 2.408 < 3 \ b2 < 3 => Given distribution is Platy Kurtosis.
|
Q (3) B) In a partially destroyed laboratory record of an analysis of a correlation data, the following results are only eligible: Variance of x=9 Regression equations: 40x-18y= 214, 8x-10y+66=0 Find i) Mean values of x and, ii) the standard deviation of y and coefficient of correlation between x and y and iii) angle between the lines of regressions Answer: Given Regression Equations are 40x-18y = 214 -------- (1) & 8x – 10y +66 = 0 --------- (2) (i) To find mean values of x and y Put x = x & y = y in given regression equations. \ 8 x – 10y = -66 40x – 18y = 214 by solving we get , x = 13 & y = 17 (ii) To find correlation r = Ö (bxy – byx) solve equation (2) for x & take of y as bxy From equation (2) => 8x = 10y-66 x =
Solve equation (1) for y & take coefficient of x as byx -18y = 214 – 40x y =
[ check : bxy . Byx <= 1 If not then swap x <--> y & Num <--> Dero bxy.byx = ( \ swap x <--> y & Num <--> Dero byx = \ ¡ = Ö (bxy. byx) = Ö ((
(iii) Var (x) = 9 & var(y) = ? \ byx =
cov.(x,y) = \ bxy =
s y = std. Deviation of y = Övar(y) = Ö16
s x = Övar(x) =Ö9 = 3
(iii) Angle between the lines of regression tanq = = = tanq = 0.512
|
Q (4) A) Find the mean and variance of binomial distribution. Answer: (A) Mean of Binomial Distribution Mean = E(x) = = = = = = np = np (p+q)n-1
=> (p+q = 1) = np (1)n-1
(B) Variance of Binomial Distribution Variance sx2 = E(x2) – [E(x)]2 \ E(x2) =
=
=
= np + = np + = np + = np +
= np + n(n-1)p2 = np + n(n-1)p2 (p+q)2 => (p+q = 1)
= np + n2p2 – np2 (1)n-2 E(x2) = np + n2p2 – np2 \variance (sx2) = E(x2) – [E(x)]2 = np + n2p2 – np2 - (np)2 =np + n2p2 – np2 - n2p2 = np(1-p) => (q=1-p)
|
Q (4) B) The probability of pen manufactured by a company will be defective is 1/10. If 12 such pens are manufactured, Find the probability that i) exactly two will be defective, ii) at least two will be defective and iii) none will be effective Answer: Total number of pens (n) = 12 Probability of a defective pen p = Probability of a non - defective pen q = 1 – p = 0.9 [ => (p + q = 1) ] (a) Probability that exactly two will be defective p(r) = ncr pr qn-r \ p(2) = 12c2 (0.1)2(0.9)12-2 =
(b) Probability that none will be defective p(0) = 12c0 (0.1)0 (0.9)12 = 1*1* (0.9)1
(c)Probability that atleast two will be defective p(2)+p(3)+p(4)+.......+p(12) = 1 – [ p(0) + p(1) ] = 1 - [ 0.2824 + 12c1 (0.1)1 (0.9)11 ] = 1 - [ 0.2824 + 0.3766 ]
|
Q (5) A) In a test of 2000 electric bulbs it was found that the life of a particular make was normally distributed with an average life of 2040 hours and SD of 60 hours. Estimate the number of bulbs likely to burn for i) more than 2150 hours, ii) less than 1950 hours, and iii) more than 1950 hours and less than 2160 hours. Answer: Given m = 2040 & s = 60 (i) For x = 2150 z = = 1.83 Area against z = 1.83 from Table = 0.4664
Required area = 0.5 – 0.4664 = 0.0336 \ The no. Of bulbs likely to burn for more than 2150 has = 0.0336 * 2000 = 67.2 » 67 bulbs (ii) Less than 1950 for x = 1950 z = Area against z = - 1.5 from Table = 0.4332 Required area = 0.5 – 0.4332 = 0.668 \ The no. Of bulbs likely to burn for less than 1950 has = 0.668 * 2000 = 153.6 »153 bulbs (iii) when x = 1950 z = = - 1.5 when x = 2160 z = p(-1.5<= z <= 2)
p(>= 1.5) = Required Area = 0.4332 & p(z<=2) = Required Area = 0.4772 \ p(-1.5<= z <= 2) = 0.4332 + 0.4772 = 0.9104 \ The no. Of bulbs likely to burn for more than 1950 hours but less than 2160 hours = 0.9104 * 2000 = 1820.8 » 1820 bulbs |
Q(5) B) Find the curve of best fit of the type y=aebx to the following data by method of least square:
Answer: Given curve y = aebx take log on both sides log y = log a + log ebx \ log y - log a + bx log e \ Y = A + B x Σ Y = nA + B Σx ----------(1)
Σ xY = A Σx + B Σx2 -------------(2) put in Equation (1) & (2) \ 5.76 = 5A + 34(B) 40.92 = 34A + 300(B) by Solving we get, A = 0.98 B = 0.025 \ log a = A \ a = 100.98 = 9.55 loge(b) = B => b = 1.06 y = aebx
|