| solved university exam paper 2019 for network theory

Back to Study material

Aryabhatta Knowledge University (AKU)Electronics and Communications EngineeringNetwork TheorySolved exam Paper 2019Question. Define the term complex frequency.Answer: A type of frequency that depends on two parameters; one is the” σ” which controls the magnitude of the signal and the other is “w”, which controls the rotation of the signal; is known as “complex frequency”.A complex exponential signal is a signal of the type

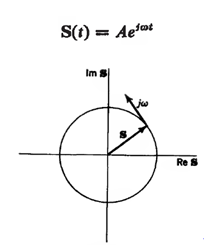
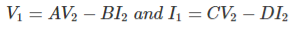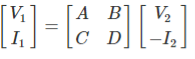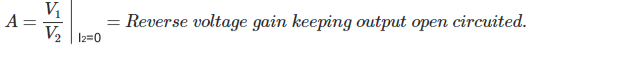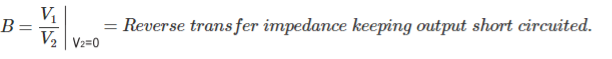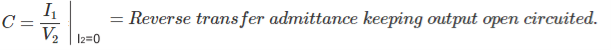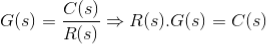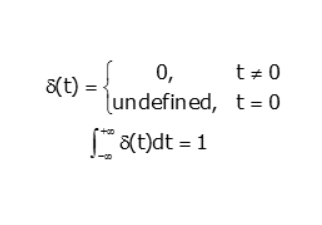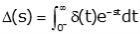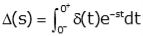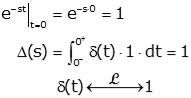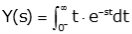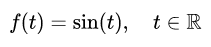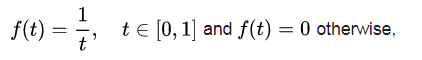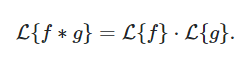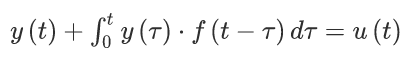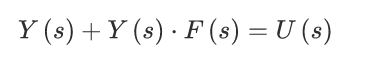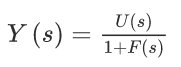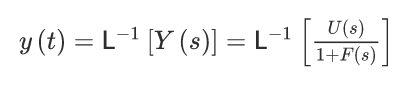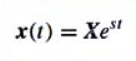Where X and s are time-independent complex parameters expressed, respectively, in polar and rectangular coordinates as

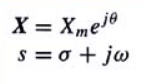This is a generalized frequency variable whose real part a describes growth and decay of the amplitudes of signals, and whose imaginary part jw is angular frequency in the usual sense. The idea of complex frequency is developed by examining the sinusoidal signal

When S(t) is represented as a rotating phasor, as shown in Fig. The angular frequency w of the phasor can then be thought of as a velocity at the end of the phasor. The velocity to be always at right angles to the phasor, as shown in Fig. However, consider the general case when the velocity is inclined at any arbitrary angle was given in Figs.

It describes the growth and decay of the amplitudes in addition to angular frequency in the usual sense. • When o = 0, the sinusoid is undamped, and where w=0, the signal is an exponential signal. Finally, if o = jw = 0, then the signal is a constant A. • Thus we see the versatility of a complex frequency descriptionQuestion. Define twig and link.Answer: Tree: A tree is a connected subgraph of a network which consists of all the nodes of the original graph but no closed paths. The number of nodes in the graphs is equal to the number of nodes in the tree. Co-tree: It is a sub graph which is formed after disconnecting a tree from the given graph.The branches of a tree are called its ‘twigs’. For a given branch, the complementary set of branches of the tree is called the co-tree of the graph. The branches of co-tree are called links, i.e., those elements of the connected graph that are not included in the tree links and forms a sub graph.

For the graph shown in the figure consider the tree branches are (b, c, d) as shown in figure.

The set of branches (e, f, g) represented by dotted lines form a co − tree of the graphs. These branches are called links of this tree.For a network with ‘b’ branches and ‘n’ nodes, the number of twigs for a selected tree is (n − 1) and the number of links ‘ℓ’ with respect to this tree is b − n + 1. The number twigs are called the rank of the tree.

These are also called transmission parameters. Here, voltage and current and of input part are expressed in term of output part.

Here,

In matrix form it can be written as,

Question. What do you mean by transfer function?Answer: A transfer function represents the relationship between the output signal of a control system and the input signal, for all possible input values. A block diagram is a visualization of the control system which uses blocks to represent the transfer function, and arrows which represent the various input and output signals.For any control system, there exists a reference input known as excitation or because which operates through a transfer operation (i.e. the transfer function) to produce an effect resulting in controlled output or response.

Thus, the cause and effect relationship between the output and input is related to each other through a transfer function.

In a Laplace Transform, if the input is represented by R(s) and the output is represented by C(s), then the transfer function will be:

That is, the transfer function of the system multiplied by the input function gives the output function of the system.

The transfer function of a control system is defined as the ratio of the Laplace transform of the output variable to Laplace transform of the input variable assuming all initial conditions to be zero.Procedure for determining the transfer function of a control system are as follows:

We form the equations for the system.

Now we take Laplace transform of the system equations, assuming initial conditions as zero.

Specify system output and input.

Lastly, we take the ratio of the Laplace transform of the output and the Laplace transform of the input which is the required transfer function.

Question. How can you say that a network is stable? Give definition.Answer: A network is strongly stable if whenever a coalition has the power to change the network to another network, the coalition will be deterred from doing so because the change is not preferred by the coalition. If coalitional preferences are strong, the change ‘not being preferred’ means that the change will not make all members of the coalition better off. If coalitional preferences are weak (i.e., based on weak preferences), the change ‘not being preferred’ means that the change will either make no members better off or will make some members better off and some members worse off. Note that under our definition of strong stability a network G ∈ G that cannot be changed to another network by any coalition is strongly stable. Question. Write down all the properties of loop impedance matrix.Answer: An Incidence Matrix represents the graph of a given electric circuit or network. Hence, it is possible to draw the graph of that same electric circuit or network from the incidence matrix.We know that graph consists of a set of nodes and those are connected by some branches. So, the connecting of branches to a node is called as incidence. Incidence matrix is represented with the letter A. It is also called as node to branch incidence matrix or node incidence matrix.If there are ‘n’ nodes and ‘b’ branches are present in a directed graph, then the incidence matrix will have ‘n’ rows and ‘b’ columns. Here, rows and columns are corresponding to the nodes and branches of a directed graph. Hence, the order of incidence matrix will be n × b.The elements of incidence matrix will be having one of these three values, +1, -1 and 0.● If the branch current is leaving from a selected node, then the value of the element will be +1.● If the branch current is entering towards a selected node, then the value of the element will be -1.● If the branch current neither enters at a selected node nor leaves from a selected node, then the value of element will be 0.Procedure to find Incidence MatrixFollow these steps in order to find the incidence matrix of directed graph.● Select a node at a time of the given directed graph and fill the values of the elements of incidence matrix corresponding to that node in a row.● Repeat the above step for all the nodes of the given directed graph. Question. Explain the following terms with reference to network topologyi. TreeTree topologies have a root node, and all other nodes are connected which form a hierarchy. So, it is also known as hierarchical topology. This topology integrates various star topologies together in a single bus, so it is known as a Star Bus topology. Tree topology is a very common network which is like a bus and star topology.

AdvantagesHere are pros/benefits of tree topology:● Failure of one node never affects the rest of the network.● Node expansion is fast and easy.● Detection of error is an easy process● It is easy to manage and maintainDisadvantagesHere are cons/drawback of tree topology:● It is heavily cabled topology● If more nodes are added, then its maintenance is difficult● If the hub or concentrator fails, attached nodes are also disabled.ii. Twig and linkThe branches of a tree are called its ‘twigs’. For a given branch, the complementary set of branches of the tree is called the co-tree of the graph. The branches of co-tree are called links, i.e., those elements of the connected graph that are not included in the tree links and forms a sub graph.iii. Incidence matrixAn Incidence Matrix represents the graph of a given electric circuit or network. Hence, it is possible to draw the graph of that same electric circuit or network from the incidence matrix.We know that graph consists of a set of nodes and those are connected by some branches. So, the connecting of branches to a node is called as incidence. Incidence matrix is represented with the letter A. It is also called as node to branch incidence matrix or node incidence matrix.If there are ‘n’ nodes and ‘b’ branches are present in a directed graph, then the incidence matrix will have ‘n’ rows and ‘b’ columns. Here, rows and columns are corresponding to the nodes and branches of a directed graph. Hence, the order of incidence matrix will be n × b.The elements of incidence matrix will be having one of these three values, +1, -1 and 0.

If the branch current is leaving from a selected node, then the value of the element will be +1.

If the branch current is entering towards a selected node, then the value of the element will be -1.

If the branch current neither enters at a selected node nor leaves from a selected node, then the value of element will be 0.

Follow these steps in order to find the incidence matrix of directed graph.● Select a node at a time of the given directed graph and fill the values of the elements of incidence matrix corresponding to that node in a row.● Repeat the above step for all the nodes of the given directed graph.ExampleConsider the following directed graph.

The incidence matrix corresponding to the above directed graph will be

The rows and columns of the above matrix represents the nodes and branches of given directed graph. The order of this incidence matrix is 4 × 6.By observing the above incidence matrix, we can conclude that the summation of column elements of incidence matrix is equal to zero. That means, a branch current leaves from one node and enters at another single node only.iv. Oriented graphIf all the branches of a graph are represented with arrows, then that graph is called as a directed graph. These arrows indicate the direction of current flow in each branch. Hence, this graph is also called as oriented graph.Consider the graph shown in the following figure.

In the above graph, the direction of current flow is represented with an arrow in each branch. Hence, it is a directed graph Question. Write the Laplace transform ofi. unit stepFrequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t.The value of t = 0 is usually taken as a convenient time to switch on or off the given voltage.The switching process can be described mathematically by the function called the Unit Step FunctionDefinition: The unit step function, is defined as

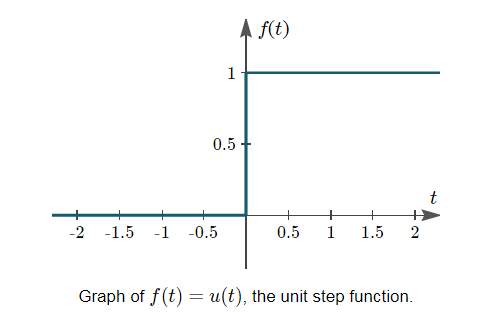
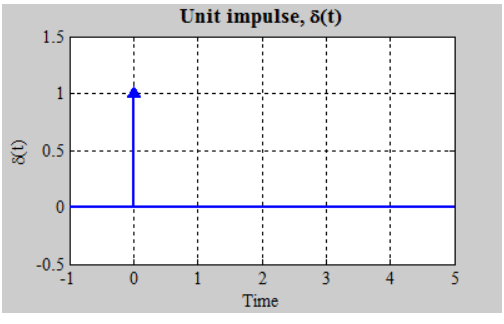
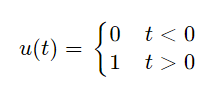That is, u is a function of time t, and u has value zero when time is negative (before we flip the switch); and value one when time is positive (from when we flip the switch).

ii. Unit impulseThe unit impulse is discussed elsewhere, but to review. The impulse function is everywhere but at t=0, where it is infinitely large. The area of the impulse function is one. The impulse function is drawn as an arrow whose height is equal to its area.

To find the Laplace Transform, we apply the definition

Now we apply the sifting property of the impulse. Since the impulse is 0 everywhere but t=0, we can change the upper limit of the integral to 0+.

Since e-st is continuous at t=0, that is the same as saying it is constant from t=0- to t=0+. So, we can replace e-st by its value evaluated at t=0.

So, the Laplace Transform of the unit impulse is just one. Therefore, the impulse function, which is difficult to handle in the time domain, becomes easy to handle in the Laplace domain. It will turn out that the unit impulse will be important to much of what we do.iii. Unit rampSo far (except for the impulse), all the functions have been closely related to the exponential. It is also possible to find the Laplace Transform of other functions. For example, the ramp function:

We start as before

Integration by parts is useful at this point

Question. Explain the following terms with the help of examplesCausal SystemA system is called causal if its output is independent of future values of input. Example of causal systems are

Non-Causal SystemA system is called noncausal if its output at the present time depends on future values of the input. Example of noncausal systems are

ii. Time variant and time invariant systemsA time-variant system is a system whose output response depends on moment of observation as well as moment of input signal application. In other words, a time delay or time advance of input not only shifts the output signal in time but also changes other parameters and behavior. Time variant systems respond differently to the same input at different times. The opposite is true for time invariant systems.Linear-time variant (LTV) systems are the ones whose parameters vary with time according to previously specified laws. Mathematically, there is a well-defined dependence of the system over time and over the input parameters that change over time.

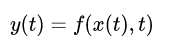In order to solve time-variant systems, the algebraic methods consider initial conditions of the system i.e. whether the system is zero-input or non-zero input systemExamples of time-variant systems● Aircraft – Time variant characteristics are caused by different configuration of control surfaces during takeoff, cruise and landing as well as constantly decreasing weight due to consumption of fuel.● The Earth's thermodynamic response to incoming Solar irradiance varies with time due to changes in the Earth's albedo and the presence of greenhouse gases in the atmosphere.● The human vocal tract is a time variant system, with its transfer function at any given time dependent on the shape of the vocal organs. As with any fluid-filled tube, resonances (called formants) change as the vocal organs such as the tongue and velum move. Mathematical models of the vocal tract are therefore time-variant, with transfer functions often linearly interpolated between states over time.Continuous and discrete-time signalsContinuous timeIn contrast, continuous time views variables as having a value for potentially only an infinitesimally short amount of time. Between any two points in time there are an infinite number of other points in time. The variable "time" ranges over the entire real number line, or depending on the context, over some subset of it such as the non-negative reals. Thus, time is viewed as a continuous variable.A continuous signal or a continuous-time signal is a varying quantity (a signal) whose domain, which is often time, is a continuum (e.g., a connected interval of the reals). That is, the function's domain is an uncountable set. The function itself need not to be continuous. To contrast, a discrete-time signal has a countable domain, like the natural numbers.A signal of continuous amplitude and time is known as a continuous-time signal or an analog signal. This (a signal) will have some value at every instant of time. The electrical signals derived in proportion with the physical quantities such as temperature, pressure, sound etc. are generally continuous signals. Other examples of continuous signals are sine wave, cosine wave, triangular wave etc.The signal is defined over a domain, which may or may not be finite, and there is a functional mapping from the domain to the value of the signal. The continuity of the time variable, in connection with the law of density of real numbers, means that the signal value can be found at any arbitrary point in time.

A typical example of an infinite duration signal is:

A finite duration counterpart of the above signal could be

The value of a finite (or infinite) duration signal may or may not be finite. For example

Is a finite duration signal but it takes an infinite value for $t=0\,$ .In many disciplines, the convention is that a continuous signal must always have a finite value, which makes more sense in the case of physical signals.Deterministic and probabilistic signalsA signal is said to be deterministic if there is no uncertainty with respect to its value at any instant of time. Or, signals which can be defined exactly by a mathematical formula are known as deterministic signals.

A signal is said to be non-deterministic if there is uncertainty with respect to its value at some instant of time. Non-deterministic signals are random in nature hence they are called random signals. Random signals cannot be described by a mathematical equation. They are modelled in probabilistic terms.

Question. State and prove convolution theorem for Laplace transform.Answer:

The convolution theorem for Laplace transform states that

The standard proof uses Fubini-like argument of switching the order of integration

The convolution theorem can be used to solve integral and integral–differential equations. Let us assume the mathematical model of a system consists of the following integral equation

where the functions f and u are known time-dependent functions and y(t) is the unknown function. Application of the Laplace transform

which is

The inverse Laplace transform of Y(s) is

Question. Explain in detail band stop filter, with proof.Answer: The band stop filter is formed when a low pass filter and a high pass filter are connected in parallel with each other. The main function of the band stop filter is eliminating or stopping the band of frequencies. The band stop filter is also referred with some other names like band-reject or notch or band elimination filter. As discussed previously, for high pass filter there will be one cut off frequency, low pass filter also has one cut off frequency but this bandpass and band stop filters have two cut off frequencies.This band stop filter will reject a range of frequencies which are there in between the two cut off frequencies. It allows the frequencies which are above the high cut off frequency and the below the low cut off frequencies. These two cut off frequencies are determined based on the value of components used in the design of the circuit. This filter has a stopband and two passbands.

The ideal characteristics of the band stop filter are clearly demonstrated in this figurefL’= cut off frequency of low pass filter‘fH’= cut off frequency of high pass filterThe working and characteristics of bandpass and band stop filters are completely opposite to each other.Band Stop Filter TheoryWhen the signal is given an input, a low pass filter allows the low frequencies to pass through the circuit and a high pass filter allows the high frequencies to pass through the circuit.

This is the block diagram of the band stop filter. Low pass filter and high pass filter are connected in parallel. There is some difference between ideal and practical conditions while working with the filter. This difference is due to the switching mechanism of a capacitor. The frequency response can be clearly explained in the above figure.Question. Explain the parallel R-L-C resonance. Give essential equations and waveforms.In many ways a parallel resonance circuit is the same as the series resonance circuit we looked at in the previous tutorial. Both are 3-element networks that contain two reactive components making them a second-order circuit, both are influenced by variations in the supply frequency and both have a frequency point where their two reactive components cancel each other out influencing the characteristics of the circuit. Both circuits have a resonant frequency point.

The difference this time, however, is that a parallel resonance circuit is influenced by the currents flowing through each parallel branch within the parallel LC tank circuit. A tank circuit is a parallel combination of L and C that is used in filter networks to either select or reject AC frequencies. Consider the parallel RLC circuit below.

Let us define what we already know about parallel RLC circuits.

A parallel circuit containing a resistance, R, an inductance, L and a capacitance, C will produce a parallel resonance (also called anti-resonance) circuit when the resultant current through the parallel combination is in phase with the supply voltage. At resonance there will be a large circulating current between the inductor and the capacitor due to the energy of the oscillations, then parallel circuits produce current resonance.Question. What do you mean by POLES and ZEROS of given network transfer function? What are the significances and limitations of network transfer function? Explain in the circuit theory.Let’s assume that we have a transfer function in which the variable s appears in both the numerator and the denominator. In this situation, at least one value of s will cause the numerator to be zero, and at least one value of s will cause the denominator to be zero. A value that causes the numerator to be zero is a transfer-function zero, and a value that causes the denominator to be zero is a transfer-function pole.Let’s consider the following example

In this system, we have a zero at s = 0 and a pole at s = –ωO.Poles and zeros are defining characteristics of a filter. If you know the locations of the poles and zeros, you have a lot of information about how the system will respond to signals with different input frequencies.Transfer function which is a control systems term but is used in almost all the fields. In short it helps to find the range of stability of any systems along with a lot more than that.In layman terms, you’ll mostly find it to be ration of output by input for any system.But a TF does more than that, electrical system for example a MOSFET or BJT amplifier. The TF of these systems give us the gain of the of the circuit, tells us its frequency response, its stability criterion; like for what range of the input will the output be stable or what will the output be, its behavior for different types of input(AC or DC) & its key features.Basically, when you find a TF of any system (circuit), you can use it to determine numerous parameters of that circuit. one can use these TF to analyse its behavior when the system is given an impulse or a step or any kind of input.Like for example an Opamp integrator, we know it’s an integrator because its TF tells us that it is. when input given is square it will integrate it and give triangular wave, only in certain range of frequency and certain values of components to keep the TF (circuit) stable.One can use operations like convolution multiplication etc., so majorly its used to determine the stability no matter what the system may be.

Question. What do you mean by ‘positive real function? What are the properties associated with PRF? What is the significance of PRF?

Positive-real functions, often abbreviated to PR function or PRF, are a kind of mathematical function that first arose in electrical network synthesis. They are complex functions, Z(s), of a complex variable, s. A rational function is defined to have the PR property if it has a positive real part and is analytic in the right halfplane of the complex plane and takes on real values on the real axis.In symbols the definition is,

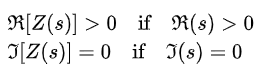In electrical network analysis, Z(s) represents an impedance expression and s is the complex frequency variable, often expressed as its real and imaginary parts;

in which terms the PR condition can be stated;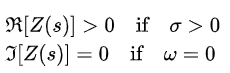

The importance to network analysis of the PR condition lies in the realizability condition. Z(s) is realizable as a one-port rational impedance if and only if it meets the PR condition. Realizable in this sense means that the impedance can be constructed from a finite (hence rational) number of discrete ideal passive linear elements (resistors, inductors and capacitors in electrical terminology).Properties

The sum of two PR functions is PR.

The composition of two PR functions is PR. In, if Z(s) is PR, then so are 1/Z(s) and Z(1/s).

All the zeros and poles of a PR function are in the left half plane or on its boundary of the imaginary axis.

Any poles and zeroes on the imaginary axis are simple (have a multiplicity of one).

Any poles on the imaginary axis have real strictly positive residues, and similarly at any zeroes on the imaginary axis, the function has a real strictly positive derivative.

Over the right half plane, the minimum value of the real part of a PR function occurs on the imaginary axis (because the real part of an analytic function constitutes a harmonic function over the plane, and therefore satisfies the maximum principle).

For a rational PR function, the number of poles and number of zeroes differ by at most one.

Question. What are the properties of Hurwitz polynomial?Network functions are the ratio of output phasor to the input phasor when phasors exist in the frequency domain. The general form of network functions is given below:

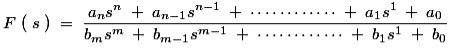Now with the help of the above general network function, we can describe the necessary conditions for the stability of all the network functions. There are three mains necessary conditions for the stability of these network functions, and they are written below:

The degree of the numerator of F(s) should not exceed the degree of denominator by more than unity. In other words (m – n) should be less than or equal to one.

F(s) should not have multiple poles on the he-axis or the y-axis of the pole-zero plot.

F(s) should not have poles on the right half of the s-plane

If above all the stability criteria are fulfilled (i.e. we have stable network function) then the denominator of the F(s) is called the Hurwitz polynomial.

Where, Q(s) is a Hurwitz polynomial.There are five important properties of Hurwitz polynomials and they are written below:

For all real values of s value of the function P(s) should be real.

The real part of every root should be either zero or negative.

Let us consider the coefficients of denominator of F(s) is bn, b(n-1), b(n-2) . . .. b0. Here it should be noted that bn, b(n-1), b0 must be positive and bn and b(n-1) should not be equal to zero simultaneously.

The continued fraction expansion of even to the odd part of the Hurwitz polynomial should give all positive quotient terms, if even degree is higher or the continued fraction expansion of odd to the even part of the Hurwitz polynomial should give all positive quotient terms, if odd degree is higher.

In case of purely even or purely odd polynomial, we must do continued fraction with the of derivative of the purely even or purely odd polynomial and rest of the procedure is same as mentioned in the point number (4).

From the above discussion we conclude one very simple result, if all the coefficients of the quadratic polynomial are real and positive then that quadratic polynomial is always a Hurwitz polynomial.

Sign Up