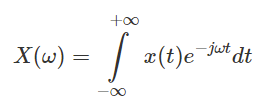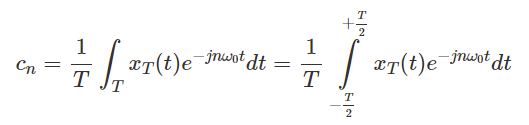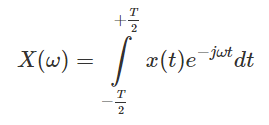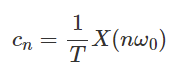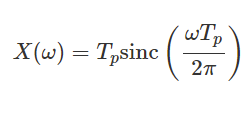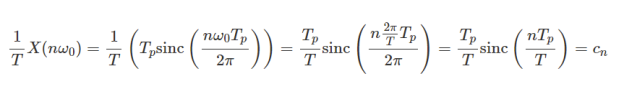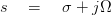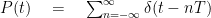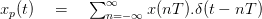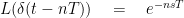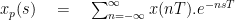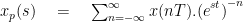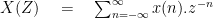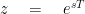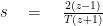The complex exponential Fourier series representation of a periodic signal x(t) with fundamental period To is given by
Since sine and cosine can be expressed in exponential form. Thus by manipulating the exponential Fourier series, we can obtain its Trigonometric form. The trigonometric Fourier series representation of a periodic signal x (t) with fundamental period T, is given by
Where ak and bk are Fourier coefficients given by
a0 is the dc component of the signal and is given by
Relationship between coefficients of exponential form and coefficients of trigonometric form
When x (t) is real, then a, and b, are real, we have
|
domain in terms of the average energy in its frequency components. Suppose if the x[n] is a sequence of complex numbers of length N : xn={x0,x1,…,xN-1}, its N-point discrete Fourier transform (DFT): Xk={X0,X1,…,XN-1} is given by
The inverse discrete Fourier transform is given by
Suppose if x[n] and y[n] are two such sequences that follows the above definitions, the Parseval’s theorem is written as
where,
|
|
|
|
The Fourier Transform of x(t) is X(ω) and is given by:
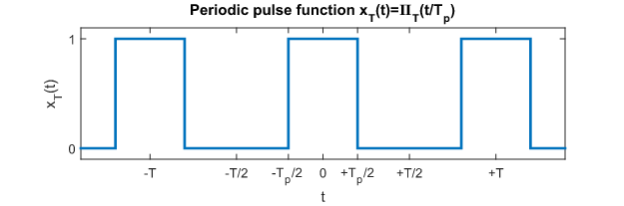
The Fourier Series coeffients, cn, of xT(T) are given by:
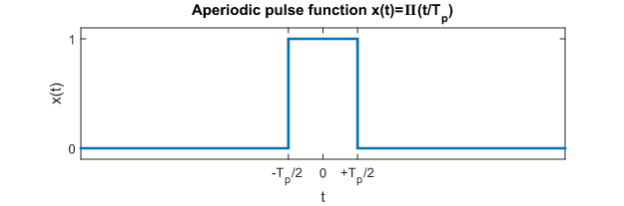
If the function x(t) is only non-zero in the inerval (-T/2, +T/2) we can rewrite the Fourier Transform as
Comparing the equations and noting the xT(t)=x(t) over the inverval of integration, we can see that the relationship between the Fourier series coefficients, cn, and the Fourier Transform, X(ω), is given by
In the particular example of the rectangular pulse
We could also get cn directly from X(ω):
|
The Laplace transform maps a continuous-time function f(t) to f(s) which is defined in the s-plane. In the s-plane, s is a complex variable defined as:
Similarly, the Z-transform maps a discrete time function f(n) to f(z) that is defined in the z-plane. Here z is a complex variable defined as:
Consider a periodic train of impulses p(t) with a period T.
Now consider a periodic continuous time signal x(nT). |
Take a product of the above two signals as shown below.
Taking Laplace transform of the above signal and using the identity Thus,
Which can be written as:
Compare this equation with that of z-transform
Thus we finally get the relation:
Another representation:
|
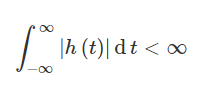
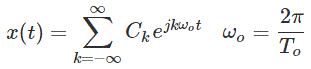
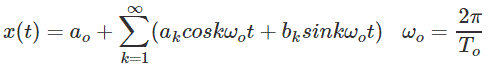
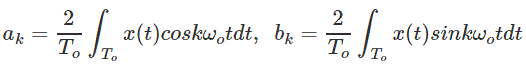
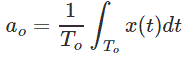
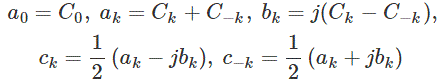
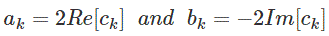
![X[k] = \displaystyle{\sum_{n=0}^{N-1} x[n] e^{-j\frac{2 \pi}{N} k n}}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642967716_331642.png)
![\tilde{x}[n] = \displaystyle{ \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j \frac{2 \pi}{N} kn}}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642967716_3973598.png)
![\boxed{ \displaystyle{\sum_{n=0}^{N-1} x[n] y^{\ast}[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] Y^{\ast}[k]}}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642967716_4442675.png)

![\begin{aligned} \sum_{n=0}^{N-1} x[n] y^{\ast}[n] &= \sum_{n=0}^{N-1} x[n] \left(\frac{1}{N} \sum_{k=0}^{N-1} Y[k] e^{j\frac{2 \pi}{N} k n} \right )^\ast \\ &= \frac{1}{N}\sum_{n=0}^{N-1} x[n] \sum_{k=0}^{N-1} Y^\ast[k] e^{-j\frac{2 \pi}{N} k n} \\ &= \frac{1}{N} \sum_{k=0}^{N-1} Y^\ast[k] \cdot \sum_{n=0}^{N-1} x[n] e^{-j\frac{2 \pi}{N} k n} \\ &= \frac{1}{N} \sum_{k=0}^{N-1} X[k] Y^\ast[k] \end{aligned}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642967716_5611937.png)